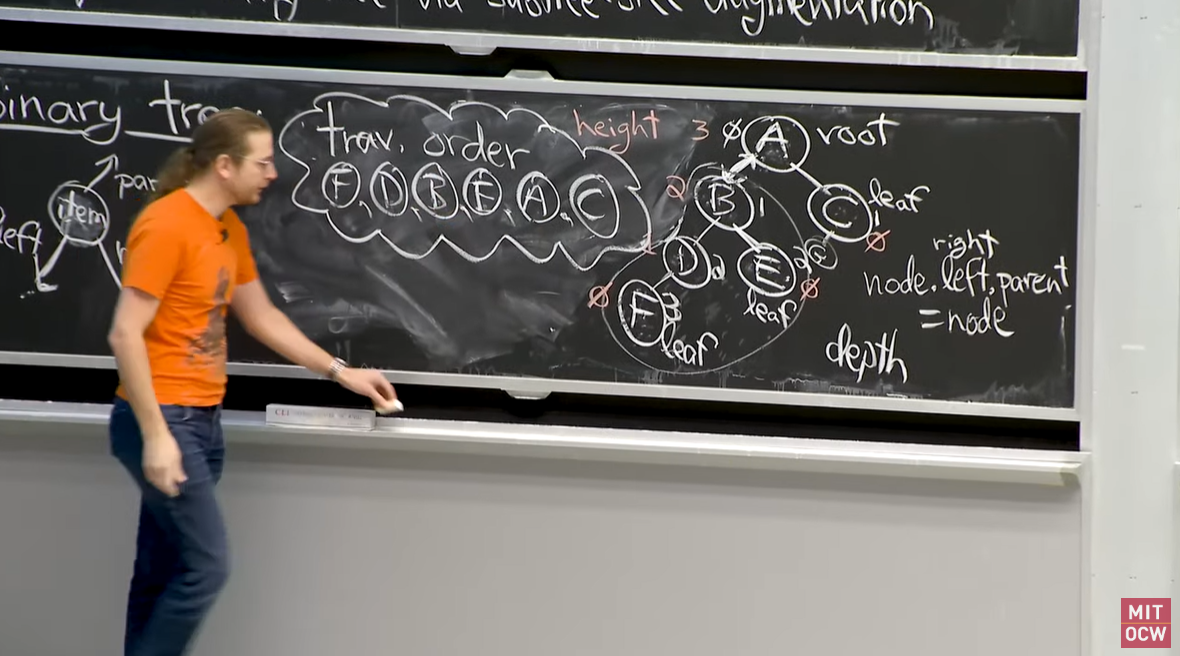
여기에 정리할 요약 노트의 원 강의는 MIT 6.006 Introduction to Algorithms, Spring 2020이다.
Binary Tree
A node in a binary tree typically has an item and three pointers: parent pointer, left pointer(child) and right pointer(child). A root is a node that does not have a parent pointer. Unlike singly or doubly linked list, you can get to a node within less than a linear time, and possibly within a logarithmic time. In a singly linked list, the item at the end has a high depth value, meaning you have to follow many pointers to get there. In a doubly linked list, you can get to the end easily but again, it takes a linear time to get to the middle of the list.
Traversal Order of a Binary Tree
A binary tree decomposes into subtrees; a subtree of x consisting of x (root of the subtree) and its descendants. It also has leaves, nodes with no children. The depth of a node is the number of its ancestors or the number of edges (an edge is a line that connects two nodes) in path from x up to the root. The height of a node is the number of edges in the longest downward path from x or the maximum depth in x’s subtree. All leaves have height of 0 and the height of the root is the same as the height of the tree.
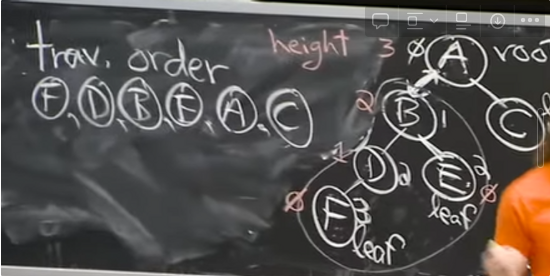
When traversing a tree, you should determine the traversal order of nodes. Suppose for every node x, nodes in x.left come before x while nodes in x.right come after x. With this particular traversal order, we can define some traversal operations:
- subtree_first(node) This operation decides which node in the subtree should come first during traversal. Here, it should go to the bottom left first(node = node.left) and return the node.
- successor(node) This operation finds the next after node in traversal. If node.right exists, meaning if the node has a right child, it should return
subtree_first(node.right). Else, walk up the tree (node=node.parent) until you go up to a left branch(node = node.parent.left) and return the node. You hitting the left branch is when the traversal direction becomes reverse.
The operations above will be O(height)
- subtree_insert_after(node.new) This operation inserts a new node so that it comes after a particular node during traversal. If there’s no node.right, put the new node there. Else, put the new node as
successor(node).left. Since the successor(node) operation goes down left as much as possible, the successor(node) is guaranteed to have no left child. This operation is O(height).
- subtree_delete(node) This operation deletes a node. If the node is a leaf, you just detach it from its parent. If the node is not a leaf, there are two cases: node.left(the target node has a left child) and node.right. In case of node.left, swap the node’s item with predecessor(node)’s item and subtree_delete(predecessor). In case of node.right, you do the same but with successor(node). This operation is O(height).
For a sequence, make the traversal order equal to the sequence order. For a set, make the traversal order equal to ordered by increasing item key. In a Binary Search Tree, you store integer key values in order. In the example order defined above, all the keys smaller than the root will be the root’s left children and those bigger will be its right children. Thus, find(k), find_previous and find_next operations are made easy.
