아키텍처 설명

Spatial data, Channel data

기존 CNN 아키텍처를 생각 해보기 전에 입력 데이터의 공간에 대해서 생각하자.

이미지에서 입력 데이터는 벡터로 표현되고 공간과 채널에 대한 3차원 데이터로 주어진다.

spatial data

공간 데이터는 이미지가 어느 공간에 있는 지를 알려준다. 예를 들어서 이미지 파일을 2차원으로 생각하면 직각 좌표를 도입해서 해당 이미지의 frame의 위치를 벡터로 표시하는 것

channel data

이미지는 색깔로 나타내는 데 빛의 삼원색인 빨, 파, 초 이 3개의 색깔의 조합으로 모든 색깔을 나타낼 수 있다. 그래서 이미지의 channel data는 빨, 파, 초 3개 중 하나만 선택한다.

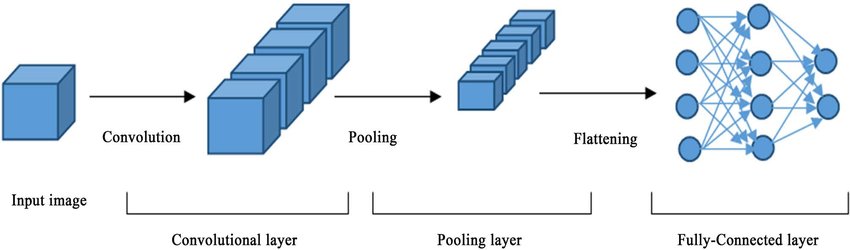
CNN 아키텍처

CNN의 전체적인 아키텍처를 살펴보지 말고 input data와 filter의 관계에 집중하자. 이번에 구현 할 mobileNetV1의 핵심 내용이 여기에 있다.

기존 CNN을 창조할 때를 생각하자. 완전 백지 상태에서 새로운 걸 만드는 과정인 데 당연히 간단한 구조에서 시작한다.

모든 입력데이터와 필터를 연산하는 게 당연하다. 왜냐면 처음 만들었으니 안전빵으로 죄다 연산하는 게 좋기 때문이다. 그걸 그림으로 보자.

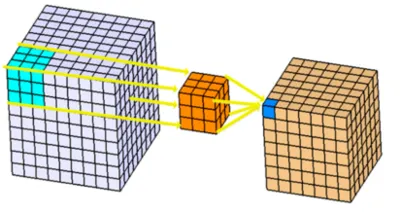
큰 박스가 입력데이터이다. 공간정보에 채널까지 3차원 박스이고 filter 역시 공간에 채널까지 3차원이라 연산은 그림과 같이 진행된다.

그런 필터의 개수가 예상하는 클래스의 개수, 즉 output channel만큼이 있는거다.

이걸 인터넷에서 찾아보면 2차원으로 설명 해놓는게 대부분 인데 3차원 박스로 이해하는 게 훨씬 쉽다.

아무튼 이런 3차원 필터를 무식하게 여러 개 만들어서 입력데이터에 학습하는 게 초기 CNN 구조이다. 그냥 무식하게 다 연산하자가 특징이다.

그럼 아주 재미없지만 연산량을 계산해보자.

mobileNet이 이 연산량을 줄여주는 건 데 원래 CNN의 연산량을 알아야 크게 공감 할 수 있다.

입력 특성 데이터: DF × DF × M, (DF, DF)는 공간데이터, M은 채널 데이터

출력 특성 데이터: DF × DF × N (DF, DF)는 공간데이터, N은 채널 데이터

합성곱 커널: DK × DK × M × N (DF, DF, M)는 공간과 채널 데이터, N은 출력 채널의 수

이걸 상상으로 박스끼리 연산하면 머리가 너무 아프다. 그냥 결과를 통해서 계산하는거다.

일단 출력 데이터를 보고 생각하자.

하나의 커널 연산의 결과가 출력 데이터의 하나의 공간 벡터로 나타난다. 그럼 하나의 벡터의 연산량에 출력 데이터 공간 크기를 곱하면 전체 연산량이다.

예를 들어서 보자.

CNN 합성곱 연산 예제

설정

• 입력 특성 맵: 5 × 5 × 3 (높이, 너비, 채널 수)
• 입력 채널 수: 3 (예: RGB 이미지)
• 출력 채널 수: 2
• 커널 크기: 3 × 3 (정사각형 커널)
• Stride: 1
• Padding: 0 (패딩 없음)

1. 출력 데이터 크기 계산

입력 데이터: 5 × 5 × 3
커널: 3 × 3 × 3 × 2
출력 데이터: 3 × 3 × 2

출력 특성 맵의 크기는 다음과 같이 계산합니다:

여기서,

• ( DF = 5 ) (입력 데이터 크기)
• ( DK = 3 ) (커널 크기)
• ( P = 0 ) (패딩 없음)
• ( S = 1 ) (Stride)

따라서,

출력 특성 맵의 크기는 3 × 3 × 2입니다.

2. 연산량 계산

각 위치에서의 연산량:

• 커널 크기: 3 × 3
• 입력 채널 수: 3

따라서, 각 위치에서의 연산량은:

전체 출력 특성 맵의 연산량:

• 출력 위치 수: 3 × 3 = 9
• 출력 채널 수: 2

따라서 전체 연산량은:

3. 일반적인 연산량 공식

일반적으로 합성곱 연산의 총 연산량은 다음과 같습니다:

여기서,

• ( DK \times DK ): 커널의 공간적 크기
• ( M ): 입력 채널 수
• ( N ): 출력 채널 수
• ( DF \times DF ): 입력 특성 맵의 크기

이 공식은 Stride와 Padding을 고려하지 않고, 입력 데이터의 모든 위치에 대해 커널이 적용된다고 가정했을 때의 연산량을 나타냅니다.

연산 핵심

1. 일단 중간 과정 생까고 output의 크기만 계산한다.

2. 그 후 output 공간 벡터 하나의 요소의 연산량을 구한다.

3. 1, 2를 곱한다.

mobileNet 아키텍처

이런 CNN의 무식한 아키텍처는 좋을까? 아님 우선 박스들의 연산이라 겹치는 부분이 굉장히 많다는 걸 느낄 수 있다. 불필요한 연산이 많다는 것이다.

mobileNet의 핵심은 이 3차원 필터 연산을 겹치는 부분이 적게 채널데이터와 공간 데이터의 연산으로 나누자는 거다.
즉 3차원 박스 연산을 2차원 연산 2개로 나눠서 나중에 합치자는 것이다.

이렇게 생각하자. CNN의 목표는 입력 데이터의 차원이 주어지면 그걸 가공해서 특정 출력데이터의 차원을 만족하는 것이니 어쨌든 출력 데이터의 차원만 맞추면 되는거 아닌가?

중간과정은 상관없이 출력데이터의 차원만 맞추면 되니까 중간과정에서 연산을 줄이자가 mobileNetV1의 핵심이다.

그 중간 과정의 연산량을(FLOPS) 줄이기 위해 맞다고 가정하는 게 있다.

채널 데이터와 공간 데이터를 나눠서 연산해도 전혀 문제가 없다는 것이다.

이건 그냥 신앙처럼 믿고 가정하는 거다. 실제로 결과가 더 좋았고

찝찝하게 수학적인 증명은 없다. 근데 결과가 좋으면 장땡인게 실험 과학의 정수라 할 말이 없음 ㅋㅋ

MobileNetV1의 Depthwise Separable Convolution

1. Depthwise Convolution

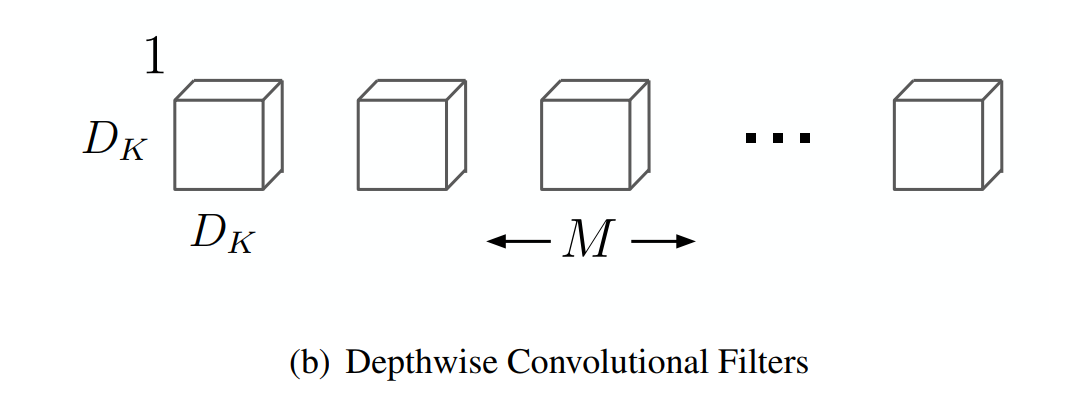
DepthWise는 채널 데이터 생각 없이 공간 데이터만 신경쓰는거다. 커널은 (공간, 공간, 채널 = 1, output 채널수)
로 입력 데이터의 각 채널을 분리해서 각각에 커널을 연산을 해주는거다.

입력 특성 맵: H × W × M
커널: DK × DK × 1 × M
출력 특성 맵: H' × W' × M

보통 CNN구조와 다르게 모든 채널에 커널이 연산하는 게 아니라 하나의 채널에 채널 개수에 맞춰서 커널을 곱해준다.

CNN의 하나의 커널이 입력데이터의 모든 채널과 연산을 한다면 mobileNet은 하나의 커널이 하나의 입력 데이터의 채널을 담당한다. 즉 커널이 output channel의 개수가 아니라 입력 데이터 채널 개수만큼 있고 각각이 입력 데이터에 채널에 일대일 대응하는 구조

연산량 계산:

각 위치에서의 연산량은:

전체 연산량은:

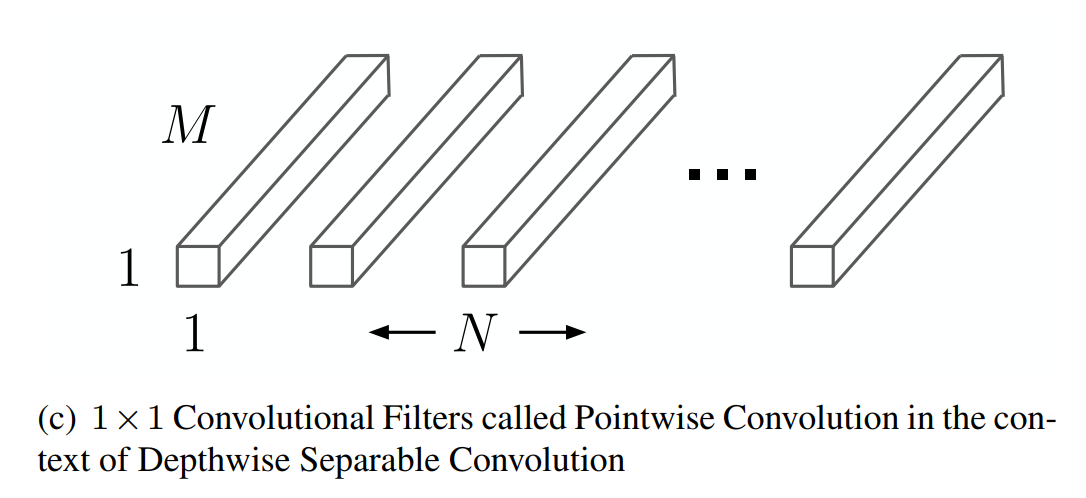
2. Pointwise Convolution

입력 특성 맵: H' × W' × M
커널: 1 × 1 × M × N
출력 특성 맵: H' × W' × N

DepthWise에서 커널의 개수가 입력데이터의 채널의 개수와 일대일로 대응해서 채널의 특징을 계산했다면 그걸 합쳐
서 연산하는걸 output 개수만큼 만드는 게 pointwise

채널의 데이터를 뽑았다면 그걸 합쳐줘야 모델의 특징이 나온다.

연산량 계산:

각 위치에서의 연산량은:

전체 연산량은:

3. 전체 연산량

MobileNetV1의 Depthwise Separable Convolution의 전체 연산량은 다음과 같습니다:

결론

CNN과 mobileNetV1의 출력 결과는

H' × W' × N이지만 중간 연산량은

으로 CNN의 모든 곱 연산을 분리해서 합 연산으로 나눠서 줄였다는게 mobileNetV1의 depthwise와 pointwise다.