주의 사항
이 글은 상당히 이론적인 글이 될 것이다. 아키텍처를 만드는 데 도움은 안되며 bottleNeck 구조의 이유에 대해서 이론적으로 다룰 글이니 넘겨도 된다.
이 글 쓴 이유
def _conv_branch(self, inputs, filter_size, is_training, count, out_filters,
ch_mul=1, start_idx=None, separable=False):
"""
Args:
start_idx: where to start taking the output channels. if None, assuming
fixed_arc mode
count: how many output_channels to take.
"""
if start_idx is None:
assert self.fixed_arc is not None, "you screwed up!"
if self.data_format == "NHWC":
inp_c = inputs.get_shape()[3].value
elif self.data_format == "NCHW":
inp_c = inputs.get_shape()[1].value
with tf.variable_scope("inp_conv_1"):
w = create_weight("w", [1, 1, inp_c, out_filters])
x = tf.nn.conv2d(inputs, w, [1, 1, 1, 1], "SAME", data_format=self.data_format)
x = batch_norm(x, is_training, data_format=self.data_format)
x = tf.nn.relu(x)
with tf.variable_scope("out_conv_{}".format(filter_size)):
if start_idx is None:
if separable:
w_depth = create_weight(
"w_depth", [self.filter_size, self.filter_size, out_filters, ch_mul])
w_point = create_weight("w_point", [1, 1, out_filters * ch_mul, count])
x = tf.nn.separable_conv2d(x, w_depth, w_point, strides=[1, 1, 1, 1],
padding="SAME", data_format=self.data_format)
x = batch_norm(x, is_training, data_format=self.data_format)
else:
w = create_weight("w", [filter_size, filter_size, inp_c, count])
x = tf.nn.conv2d(x, w, [1, 1, 1, 1], "SAME", data_format=self.data_format)
x = batch_norm(x, is_training, data_format=self.data_format)
else:
if separable:
w_depth = create_weight("w_depth", [filter_size, filter_size, out_filters, ch_mul])
w_point = create_weight("w_point", [out_filters, out_filters * ch_mul])
w_point = w_point[start_idx:start_idx+count, :]
w_point = tf.transpose(w_point, [1, 0])
w_point = tf.reshape(w_point, [1, 1, out_filters * ch_mul, count])
x = tf.nn.separable_conv2d(x, w_depth, w_point, strides=[1, 1, 1, 1],
padding="SAME", data_format=self.data_format)
mask = tf.range(0, out_filters, dtype=tf.int32)
mask = tf.logical_and(start_idx <= mask, mask < start_idx + count)
x = batch_norm_with_mask(
x, is_training, mask, out_filters, data_format=self.data_format)
else:
w = create_weight("w", [filter_size, filter_size, out_filters, out_filters])
w = tf.transpose(w, [3, 0, 1, 2])
w = w[start_idx:start_idx+count, :, :, :]
w = tf.transpose(w, [1, 2, 3, 0])
x = tf.nn.conv2d(x, w, [1, 1, 1, 1], "SAME", data_format=self.data_format)
mask = tf.range(0, out_filters, dtype=tf.int32)
mask = tf.logical_and(start_idx <= mask, mask < start_idx + count)
x = batch_norm_with_mask(
x, is_training, mask, out_filters, data_format=self.data_format)
x = tf.nn.relu(x)
return xhttps://github.com/melodyguan/enas/blob/master/src/cifar10/general_child.py
를 참고해서 Enas를 구현 중 인데 conv브랜치를 만드는 중요한 매서드가 처음부터 pointwise를 집어넣고 있다. 논문에는 언급되지 않은 부분이라 당황했지만 지난 논문들을 살펴본 결과 이것이 bottleNeck 구조란걸 알았다.
이 bottleNeck 구조를 이용한 게 shuffleNeck, mobileNetV2의 Inverted Residual block 등이 있다.
논문은 내가 알기로 2018년도에 발행하여 막 bottleNeck구조를 이용한 시점으로 보이고 위 코드의 구현 또한 초기 bottleNeck 구조를 보여주고 있다. 아마 앞으로 구현은 이 bottleNeck 구조가 아닌 Inverted Residual block으로 구현할 것이지만 bottleNeck 구조는 우리가 이미 구현한 Inverted Residual block의 중요한 원리이므로 오늘은 bottleNeck 구조의 이론에 대해서 간단하게 알아보겠다.
딥러닝의 목표
일반적인 딥러닝의 목표는 어떤 데이터를 학습해도 범용성 있고 그러면서도 정확한 모델을 만드는 것이다.
이 두 가지 목표는 당연히 상충된다. 범용성을 따지면 사실 매우 정확한 예측은 불가능 하다. 매우 정확한 모델은 특정 데이터에 매우 정확하다는 말로 다른 데이터에 대해선 정확성이 떨어진다는 말이다.
컴퓨터가 범용성과 정확성을 동시에 챙길려면 많은 리소스를 투입해야 한다. 사실은 불가능한 방법이다.
인공지능이 활발히 발달되고 있는 지금 이 시점부터 리소스가 너무 많이 들어간다는 문제점이 부각되고 있다.
따라서 기본적인 딥러닝의 방향성은 제한된 리소스에서 적절한 밸런스를 찾는것이다.
리소스를 제한하는 점에서 컴퓨터의 특징을 살펴보자.
컴퓨터는 기본적으로 해석적이 아닌 이산적인 근사값을 구해야한다.
해석학적인 함수는 보통 목표 함수를 무한한 함수의 합으로 표현한다. 예를 들어서 푸리에 해석은
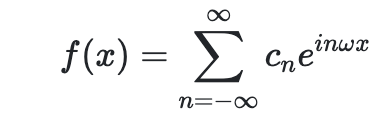
위와 같이 무한한 함수의 합을 통해서 수렴하는 함수를 찾는 방법이지만 컴퓨터는 리소스의 한계 때문에 이럴수가 없다.
우리 딥러닝의 목표는 위 급수의 범위를 무한대가 아닌 유한한 급수로 근사해서 푸는 것과 같이 이산적으로 풀면서 밸런스 있게 급수를 만드는 것이다.
데이터의 압축(IB, Information Bottleneck)
딥러닝의 목표가 모델의 범용성과 정확성의 밸런스를 맞추는 것이다.
이 목표를 이루기 위한 아이디어가 입력 데이터의 압축이다.
결국엔 모델이 예측하는 건 데이터를 기반으로 하므로 범용성과 정확성을 동시에 챙기기 위해선 데이터의 집합에서 공통되고 중요한 데이터만 남기는 것이 중요하다. 이걸 데이터의 압축이라고 한다.
용어 정의
입력 데이터를 X라고 하고 출력 데이터를 Y라고 두자.
우리의 목표는
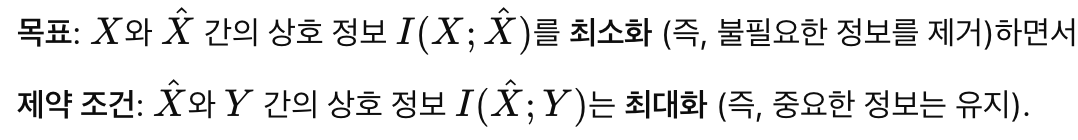
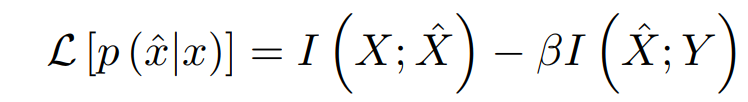
위와 같은 라그랑지안의 최소값을 찾는 것이다.
엔트로피
물리학에서 많은 분자의 운동을 표현하기 위해서 만든 개념으로 계 안의 분자의 분포 상태를 살펴보기 위한 개념이었으나 새넌이 정보이론을 만들면서 사용함.
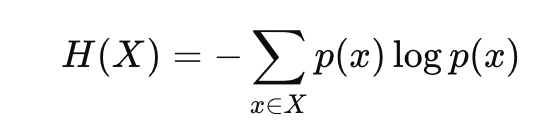
정보이론에서 엔트로피는 위와 같이 정의된다.
어떻게 유도 되었는가는 물리학적으로 설명할 수 있지만 아무도 관심 없을 걸 안다.
엔트로피는 어떤걸 의미하나? 확률의 분포를 대충 알 수 있다.
예를 들어서 확률분포가 아주 고르다면 엔트로피는 최대값이 되는데 확률 분포가 고르다는 말은 뭐가 뽑힐지 불확실하다는 것.
반대로 확률분포가 아주 뾰족하고 나머지 부분은 거의 0에 가깝다면 엔트로피는 작은 값이며 누가 봐도 뾰족한 구간이 뽑히니 확실하다는 것
조건부 엔트로피
조건부 엔트로피는 변수 X의 엔트로피를 Y가 주어졌을 때 측정하는 척도
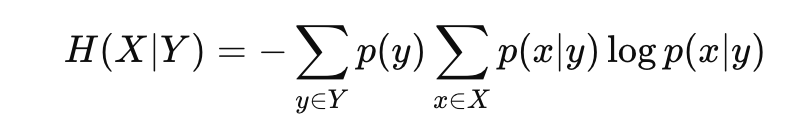
조건부 식을 결합만하면 된다.
Y가 x의 정보를 모두 담고 있다면 0, 아무것도 모른다면 H(X)가 된다.
상호정보(Mutual Information)
상호 정보는 X에 대한 불확실성이 Y를 통해 얼마나 줄어드는지를 나타내는 척도
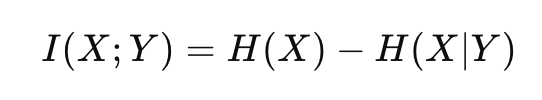
I가 상호정보를 나타내며 앞으로 설명할 때 자주 나올 예정이다.

정의와 엔트로피들의 정의를 겹합해서 계산하면 아래와 같은 식이 나온다.
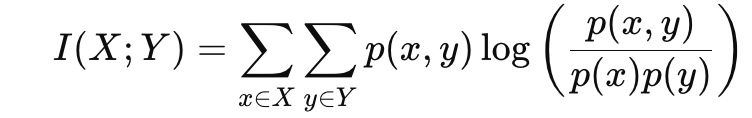
마르코프 체인
마르코프 체인은 기본적으로 조건부 독립성을 정의하는데 사용된다
마르코프 체인 T−X−Y는 다음과 같은 의미를 가진다.
T는 X를 통해 Y와 연결되며, 이때 T와 Y는 직접적인 의존성이 없다.
마르코프 체인의 순서에 관한 의미는 인접한 인자의 의존성을 말한다.
즉 각 변수가 이전 변수에만 의존한다는 것을 뜻한다.
예를 들어서 마르코프 체인 T−X−Y는
- T는 X에 의존
- Y는 X에 의존
- X는 T, Y에 의존
그냥 인접한 인자끼리 서로 의존한다고 생각하면 된다.
이 마르코프 체인은 정보이론에서 잘 쓰인다잉
다시 목표로
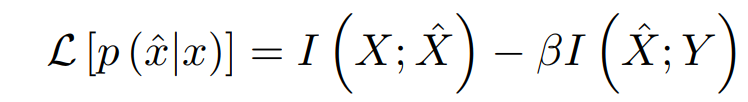
그럼 이건 어떻게 나온 값 인가? 우리가 방금 T로 표현했으니까 T로 다시 표현해보자.
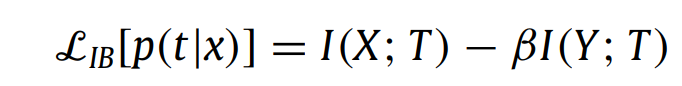
X는 입력데이터, Y는 출력데이터, T는 우리가 필요한 입력데이터의 Target으로 우리의 목표인 X에서 필요한 부분만 압축된 데이터이다.
다시 목표로 돌아가면 최대한 압축되면서 출력 데이터와 가장 연관된 T를 찾으면 된다는 말이다.
앞서 말했듣이 I는 연관된 정도를 뜻하므로 T는 X를 제한조건을 지키면서 X를 최대한 압축한 값이니 X와 T는 최대한 연관성이 적고 Y와 T는 연관성이 최대한 많아야 한다.
즉 위 식에서 최소값을 찾으면 적절한 T를 찾을 수 있다는 말이다. T는 X와 Y에 모두 연관되어 일종의 제한 조건을 만드므로 라그랑지안을 이용해서 T를 찾는다.
라그랑지안에 관한 건 미적분학을 찾아도 좋고 고전 물리학을 찾아봐도 좋다. 내 생각엔 미적분학이 더 이해하기 쉬울 듯
B(B>0) 의 경우엔 제약조건을 조절하는 변수로 생각하면 된다.
풀이법
앞서 말했던 목표인 라그랑지안을 풀어보자.
용어 정의에서 보여줬던 식을 라그랑지안에 대입하면 아래와 같다.
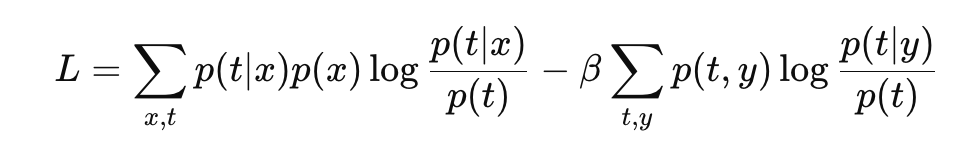
우리는 p(t∣x) 최적화 시켜야 한다. 따라서 라그랑지안을 p(t∣x)의 변분법으로 풀자.
첫 번째 항을 변분하면
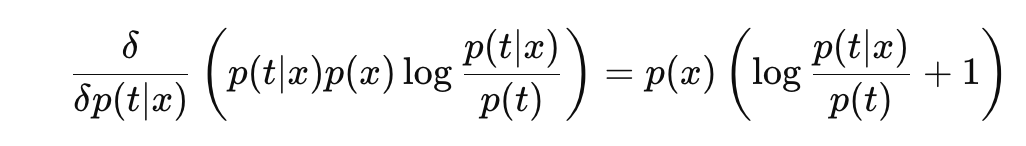
두 번째 항을 변분하기 위해서 식을 변형해서 변분 해주면
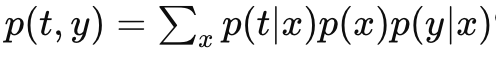
KL 발산에 관한 식을 이용해서 변분법을 풀자. 아래와 같은 식을 이용하면
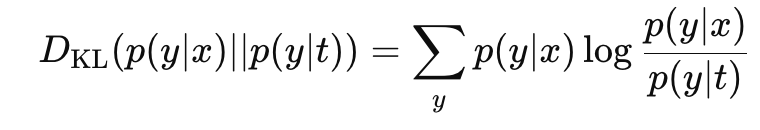
다음과 같은 식을 얻는다.
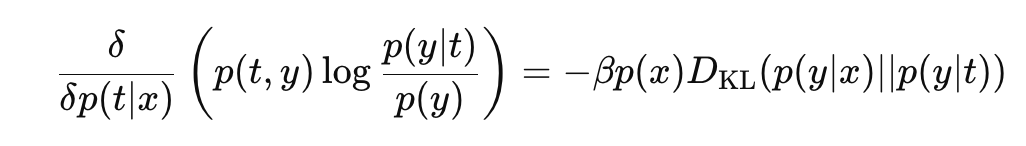
좌항과 우항을 결합하면 아래와 같다.
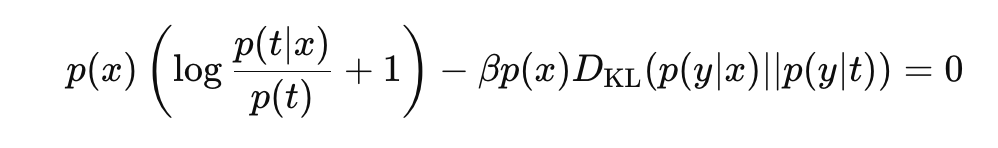
아래와 같이 항을 정리해주자.
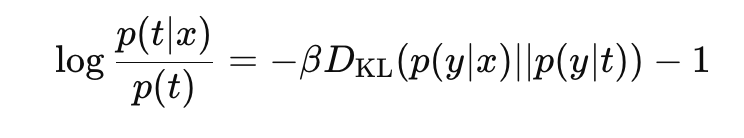
그리고 양변에 지수를 취해준다.
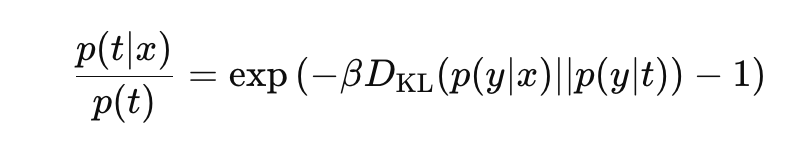
그러면 아래와 같은 결론을 얻을 수 있다.
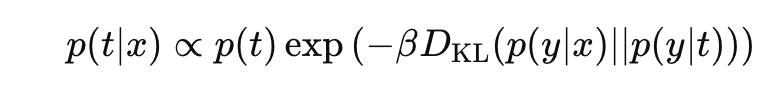
이제 위 식을 확률로 만들기 위해서 정규화 해주자.
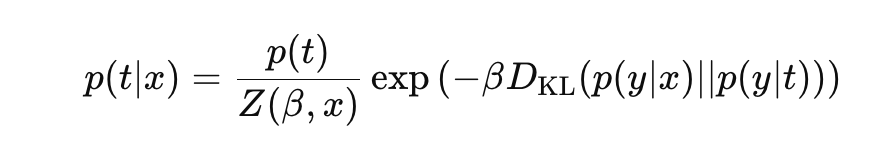
Z는 정규화 상수로 다음과 같다.
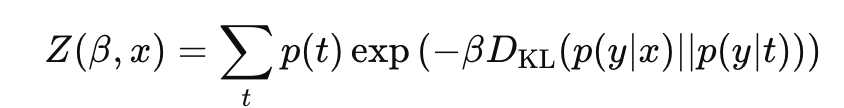
결과를 정리해자면 최적화를 위해 라그랑지안을 풀면 다음과 같은 결과를 얻는다.
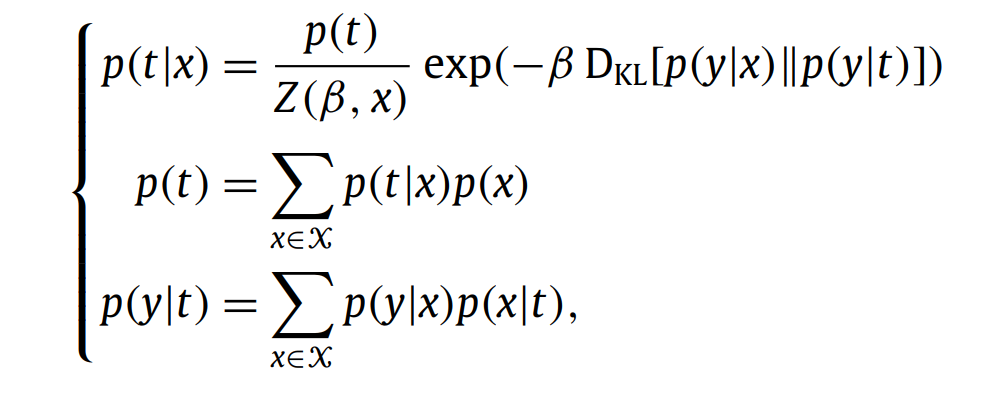
중요한 결론 β
내가 이 시리즈에 필요 없어보이는 이 글을 왜 작성 했을까?
이런 정보 압축 이론은 그래서 어떤 점이 딥러닝 측면에서 중요한건가?
앞선 시리즈에서 mobileNetv2의 inverted Residual block을 보면서 pointwise와 relu를 이용한 manifold of interest란 결과를 보았다.
경량화은 크게 3가지 측면이 있다.
- 정보 압축
- 계산량 단축
- accuracy와 latency의 밸런스
여기서 정보 압축 이론의 이론적인 토대가 이 글의 내용이다.
결론에서 β의 의미는 그럼 뭐냐?
우리가 bottleNeck 구조에서 pointwise를 이용해서 정보 압축을 하게 되는데 이때 pointwise의 결과물이 T라고 생각할 수 있다. 정보를 얼마나 압축하는가? 어떻게 최적의 결과를 도출할 것인가? 내가 어떻게 이 정보 압축을 모델에 알맞게 조절 할 건가?
이 모든걸 결정하는 게 β다.
이 글에서 참고한 논문은 3갠데 결과에 따르면 다음과 같은 사실을 알 수 있다.
β ≤ 1 일 때
카디널리티가 1인 trivial한 T도 최적해가 될 수 있다.
즉, 이 경우에는 T가 매우 단순해질 수 있으며, T가 어떤 정보를 갖고 있는지에 상관없이 상수 값만 가질 수도 있다.
모델이 입력에서 가능한 한 많은 정보를 버리고, 단순한 표현을 선호하는 방법이다.
모델이 불필요한 세부 정보를 무시하고 중요한 특징만 남긴다.
β가 커질 때
하지만 β가 증가하면, T가 Y에 대한 정보를 전달하는 역할이 더 중요하다. 즉, T가 Y에 대해 더욱 많은 정보를 제공해야 하므로, T의 카디널리티가 증가하게 된다. 따라서 T의 다양성이 증가한다.
모델이 Y에 대한 정보를 최대한 유지하려고 하므로, 더 복잡하고 세부적인 특징 표현을 만들게 됩니다.
결론적으로 압축은 하되 거의 압축하지 않아서 출력을 좀 더 세밀하게 만들자는 방법
요약

