Uncovering High-Order Cohesive Structures: Efficient (𝑘,𝑔)-Core Computation and Decomposition for Large Hypergraphs

Abstract

• Cohesive subgraph discovery
• Selecting appropriate parameters is an open question
• Aim to design an efficient indexing structure to retrieve cohesive subgraphs

---

1. Introduction

Limitation of existing approaches

• Existing approaches primarily handle pairwise relationships, relying on indirect representations of higher-order structures such as motif and cliques
• To better capture higher-order structures beyond pairwise interactions, hypergraphs have emerged as a more flexible structure where a single hyperedge can connect multiple nodes simultaneously
• $k$-hypercore only consider neighbor constraint
• $(k,d)$-core incorporates a degree constraint
  Assumes that if any node in a hyperedge is removed, the hyperedge must also be discarded

Co-occurrence pattern

• Accounts for the frequency of repeated interactions between nodes in hypergraphs

---

2. Problem Statement

Notations and Definition

• $deg(v)$: the count of hyperedges containing $v$
• $|e|$: the number of nodes in $e$

Def 1. Support

• Support value $s(u,v)$ with two nodes $u,v \in V$ is the number of hyperedges in which both nodes co-occur

Def 2. 𝑔-Neighbour

• Given a node $u \in V$, and a support threshold $g$, a node $v \in V$ is called a $g$-neighbour of $u$ if the support value between $u$ and $v$ is greater than or equal to $g$,
  i.e., $s(u,v) \geq g$
• Set of $g$-neighbours of a node $u$ as $N_g(u)$

Def 3. (𝒌, 𝒈)-core

• Given a neighbour size threshold $k$ and a support threshold $g$, $C_{k,g}$ is the maximal set of nodes where each node has at least $k$ neighbour nodes as its $g$-neighbours within $G[C_{k,g}]$

---

Key properties of the (𝒌, 𝒈)-core

1. Uniqueness of $(k,g)$-core

• The maximal subset of nodes satisfying the given $k$ and $g$ constraint within the hypergraph is unique

2. Containment of $(k,g)$-core

• A hierarchical structure, meaning that both the $(k+1,g)$-core and the $(k,g+1)$-core are contained within the $(k,g)$-core

---

3. (𝒌, 𝒈)-core Computation

Efficient Peeling Algorithm (EPA)

• The naive approach maintains an explicit $g$-neighbour set for every node and continuously updates the pairwise co-occurrence counts
• EPA only tracks the number of $g$-neighbours for each node

Pseudo Code

• Intially for each node, the size of its $g$-neighbour is computed and recorded (4-6)
• Nodes that do not satisfy the $(k,g)$-core criteria are identified and marked for removal (7-8)
• The number of $g$-neighbours for each affected node is updated (13-15)
• The final set of nodes constitutes the $(k,g)$-core

---

Time Complexity

• $O(|e^*|\cdot D)$
• $D$ : the total sum of the degree of all nodes in the hypergraph
• $|e^*|$ : the maximum cardinality among all hyperedges

• To compute the $g$-neighbours of a single node $v$, examines each hyperedge containing $v$ ($deg(v)$ such hyperedges)
• Iterates through up to $|e^*|$ nodes to identify those that co-occur with $v$
• Resulting in a time complexity of $O(|e^*| \cdot deg(v))$
• Considering all nodes, the total becomes $O(|e^*| \cdot D)$

Space Complexity

• $O(|V|)$
• Store only the size of $g$-neighbours

---

4. (𝒌, 𝒈)-core Decomposition

4.1. Coreness of the (𝒌, 𝒈)-core

• The coreness of a node refelcts the maximum level of $(k,g)$-core that the node can belong to,
  indicating the intensity of engagement of each node within the network

Def 4. $k$-coreness

• Given a positive integer $k$, the maximum integer $g'$ for which $v$ belong s to the $(k,g')$-core but not to the $(k,g'+1)$-core
• The $k$-coreness indicates maximal co-occurrence frequency that a node can have

Def 5. $g$-coreness

• Given a positive integer $g$, the maximum integer $k'$ for which $v$ belong s to the $(k',g)$-core but not to the $(k'+1,g)$-core
• The $g$-coreness represents the highest levels of neighbour connectivity

Def 6. $(k,g)$-coreness

• Given a node $v \in V$, the $(k,g)$-coreness of a node $v$ is the maximal $(k,g)$ pairs such that $v$ is in the $(k,g)$-core
  but not in the $(k',g)$-core or the $(k,g')$-core, where $k'>k$ and $g'>g$
• A node can have multiple $(k,g)$-coreness values as long as each is maximal

---

4.2. Bucket-based decomposition algorithm

Bucket-based Coreness Algorithm (BCA)

1. Enumerate all possible $(k,g)$-cores
2. Remove duplicates by leveraging the hierarchical properties of the $(k,g)$-core

Pseudo Code

• Initially, $k$ is set to 0 and $g$ to 1
• For each node, the number of $g$-neighbours is computed and nodes are assigned to buckets (5-10)
  Can focus on only those nodes whose $g$-neighbour count falls below a $k$ threshold rather than checking all nodes
• Nodes that do not satisfy the $k$ constraint are marked for removal (14-20)
• After reducing their $g$-neighbour count by one, the $g$-neighbours of the removed nodes are reassigned to the buckets (21-27, 32)
• Any node whose updated $g$-neighbour count falls below $k$ is also marked for removal and deleted in the next iteration (28)

DedDuplication

• If the node appears in a higher core value, it is removed from the current core

---

Time Complexity

• $O(g^* \cdot |e^*| \cdot D)$
  • $g^*$ : the maximum $g$ value
• The process iterates up to $g^*$
• Each iteration involves at most $|e^*| \cdot D$ computations

Space Complexity

Three factors

• Storing the $(k,g)$-coreness of each node
• Maintaining the count of $g$-neighbours
• Grouping nodes based on their $g$-neighbour count

• Storage requirement of the $(k,g)$-coreness for every nodes is $O(min(k^*,g^*)|V|)$
• Storing the number of $g$-neighbours for each node requires $O(|V|)$ space
• Additionally, grouping can store up to $O(|V|)$ nodes
• $\therefore O(min(k^*,g^*)|V|)$

---

5. Experiments

5.2 Experimental Setting

• $k$-hypercore, nbr-$k$-core and $(k,d)$-core identify strongly induced subgraphs, which means that any node removed must also discard all hyperedges containing it

---

5.3 Experimental Results

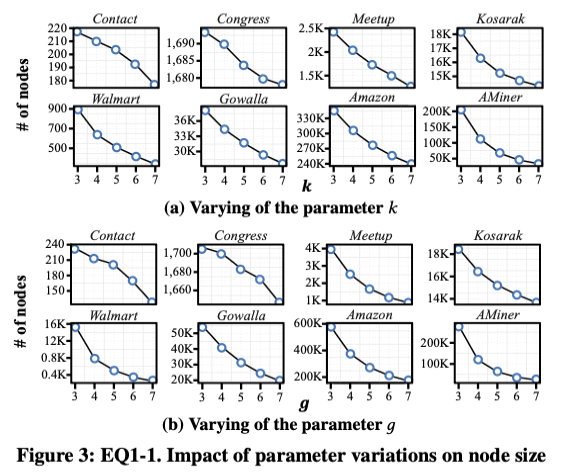
EQ1. Impact of Parameter Variations on Subhypergraph Co-hesion

• To observe the impact of changing $g$ while keeping $k$ constant, fix $k$ and vary $g$ over the values 3~7
  Similarly, fix $g$ and vary $k$

• In the Contact dataset, the average degree drops when $g$ reaches 7
  This occurs due to a substantial reduction in hyperedges resulting from stricter co-occurence constraints

---

EQ2. Running Time with Varying Parameters

EQ5. Comparison of $(k,g)$-core with other models

• By incorporating both degree and co-occurrence constraints, resultant groups are dense subhypergraphs

EQ7. Distribution of $(k,g)$-coreness and $(k,d)$-coreness

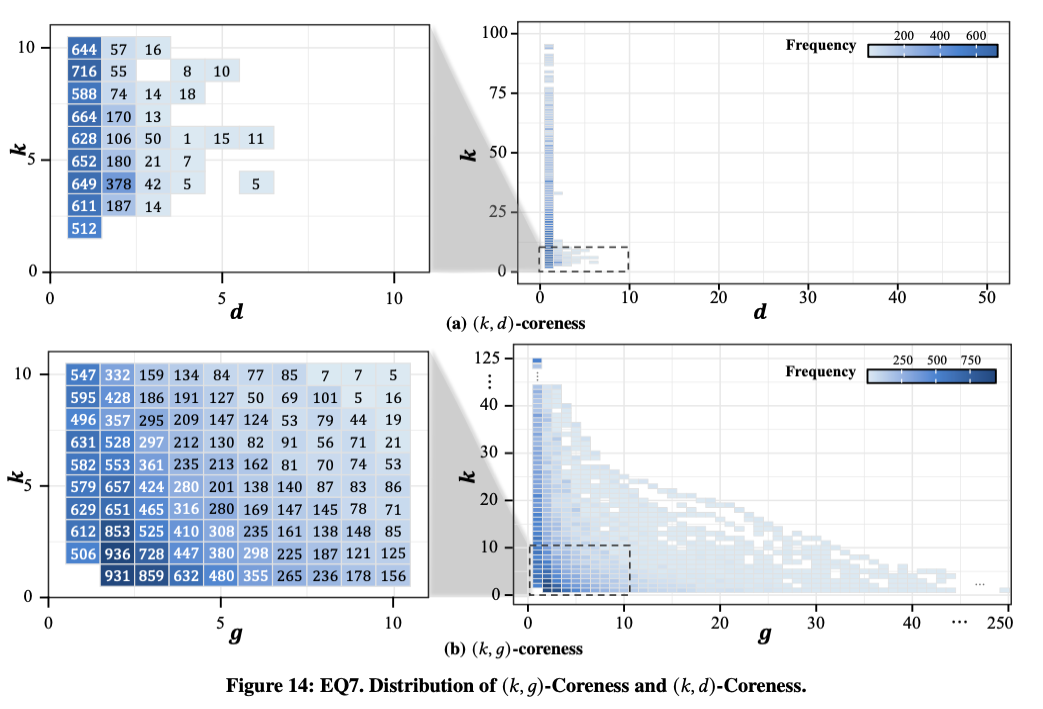
• $(k,g)$-core enables more granular hierarchies, capturing a broader spectrum of internal cohesion levels