Finding Critical Users for Social Network Engagement: The Collapsed k-Core Problem

Background

K-core

• Remaining maximal sub-graph, after iteratively pruning nodes which have less than k degrees
• Indicates the influence of node
• Unique in one graph

---

Abstract

• In social networks, the leave of critical users may break network engagement
• A popular model to measure social network engagement is k-core
• To identify critical users for social network engagement, propose the collapsed k-core problem
  • Given a graph $G$, a positive integer $k$ and a budget $b$,
    aim to find $b$ vertices in $G$ such that the deletion of the $b$ vertices leads to the smallest k-core
• Proposal : An efficient algorithm which significantly reduces the number of candidate vertices to speed up the computation

---

Introduction

k-core

• k-core is a simple and popular model based on degree constraint used to measure the network engagement
• A user with less than $k$ friends engaged will drop out, and his leave may be contagious

collapsed k-core problem

• Given a limited budget $b$, how to find $b$ vertices(users) so that we can get the smallest k-core by removing these $b$ vertices
  = then, these $b$ appears to be influencial
• Aims to collapse the engagement of the network with the greatest extent for a given budget $b$
• Identifying critical users
  = Identifying most valuable users to sustain or destroy the engagement of the networks
• Also, we can evaluate the robustness of network engagement against the vertex attack

Example

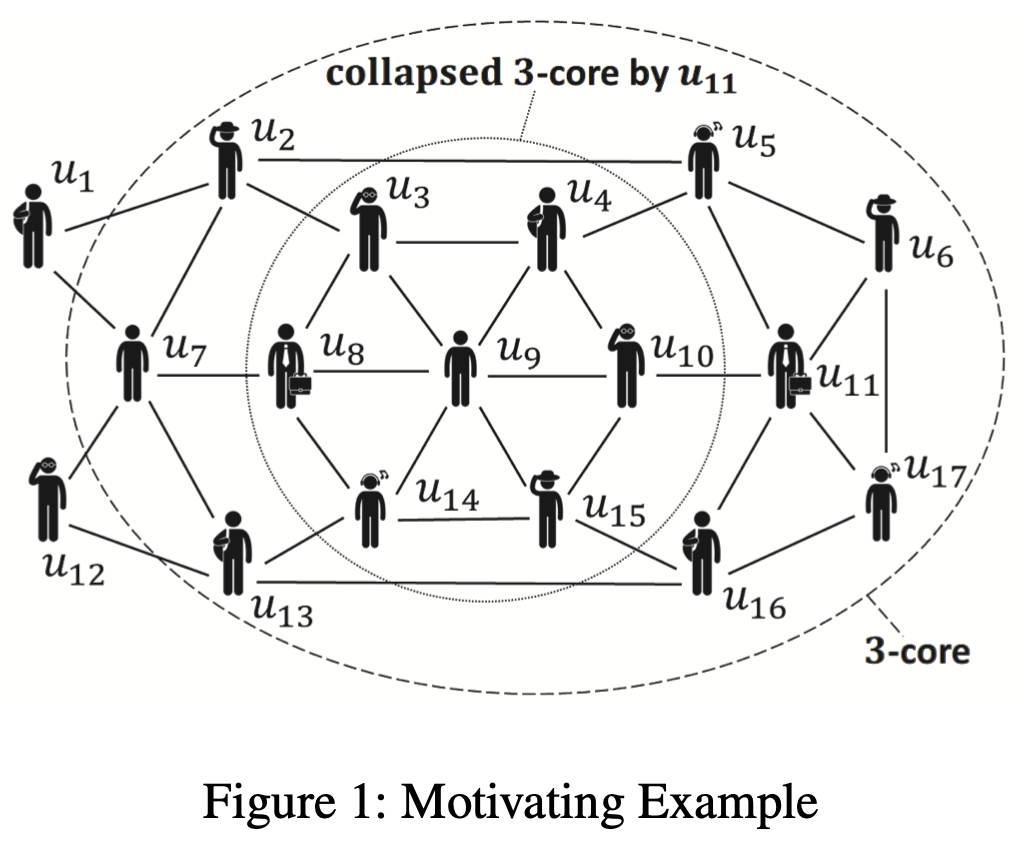
• The extent of the collapse varies among different users
  • Although $u_9$ has 6 friends in 3-core, the departure of $u_9$ will not further lead to the leave of the other users
  • On the contrary, the leave of $u_11$ will lead to the leave of 7 members
  • In this sense, it is more cost-effecitve to give $u_11$ the incentive to ensure to his/her engagement to leave the group

Challenges and Contributions

• First proposal to handle the collapsed k-core problem
• Resort to greedy heuristics where the best vertex is obtained in each iteration
• Through theoretical analyses, significantly reduce the number of candidate vertices to speed up the computation

---

Preliminaries

Notation

k-core

• The k-core of a graph can be obtained with $O(m)$
• The value of $k$ is determined by users based on their requirement for cohesiveness
  The resulting k-core will be more cohesive if the $k$ value becomes larger

collapsed k-core

• In addition to the deletion of the collapsed vertices in $A$, more vertices in $C_k(G)$ might be deleted due to the contagious nature of the k-core
• These vertices are called followers of the collapsed vertices $A$
• The size of the followers reflects the effectiveness of the collapsed vertices

Problem Statement

• Given a graph $G$, a degree constraint $k$ and a budget $b$,
  Find a set $A$ of $b$ collapsed vertices in $G$ so that
  the size of the resulting collapsed k-core, $C_k(G_A)$ is minimized,
  that is, $F(A,G)$ is maximized

---

Complexity

Theorem 1. The collapsed k-core problem is NP-hard for any $k$

$k=1$

• Reduce Collapsed 1-core Problem to Maximum Independent Set Problem
• Maximum Independent Set
  • 그래프에서 서로 연결되지 않은 정점들 중 최대한 많은 수를 찾는 문제
  • 임의의 두 정점 $u,v \in S$ 에 대해 $(u,v) \notin E$ 이어야함
• Reduction
  1. 1-core 에서 임의의 정점 $v$ 를 제거하려면 $v$ 의 모든 이웃 제거 필요
  • $\rightarrow$ $v$의 차수 = 0
  2. $S$ 가 Independent Set 이라면
  • $S$ 내의 정점들은 서로 연결되어 있지 않음
  • = $G \backslash S$ 에는 모든 간선이 몰려 있음
  3. $G \backslash S$ 를 제거하면
  • $S$ 에 있는 모든 정점은 더 이상 연결된 간선이 없음 ($\rightarrow$ 차수=0)
  • 따라서 1-core 에서 $S$ 에 속한 모든 정점이 탈락
  4. 즉, $S$ 를 살리고 $G \backslash S$를 제거하면 전체 1-core 가 붕괴

$k=2$

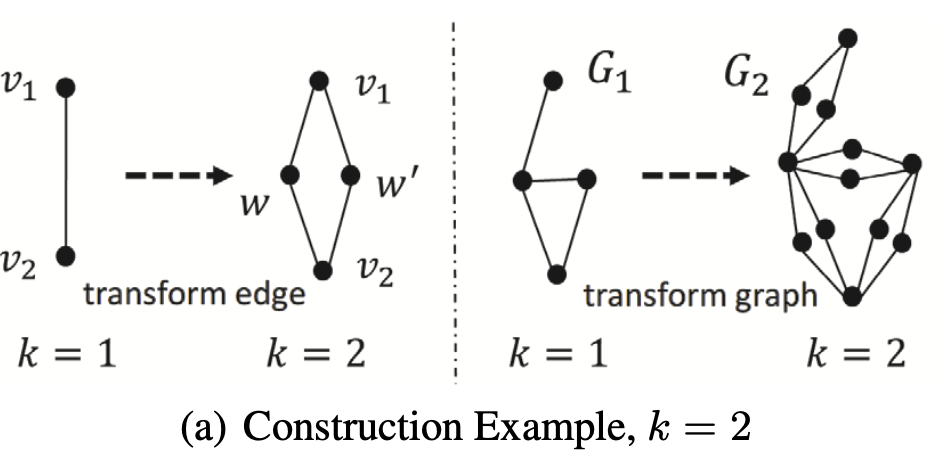
• Reduce Collapsed 2-core Problem to Collapsed 1-core Problem
• Reduction
  • Given graph $G_1$, construct another graph $G_2$
  • Each edge $(v_1,v_2)$ in $G_1$, add two virtual vertices $w$ and $w'$ and construct four edges in $G_2 : (v_1,w), (w,v_2), (v_1,w'), (w',v_2)
  • Do not need to include any virtual vertices in the optimal solution of collapsed 2-core
    because the influence of deleting a virtual vertex can be covered by deleting non-virtual vertices
  • Therefore, deletion of edge in $G_1$ is mapped to the deletion of four edges in $G_2$
    

$k\geq 3$

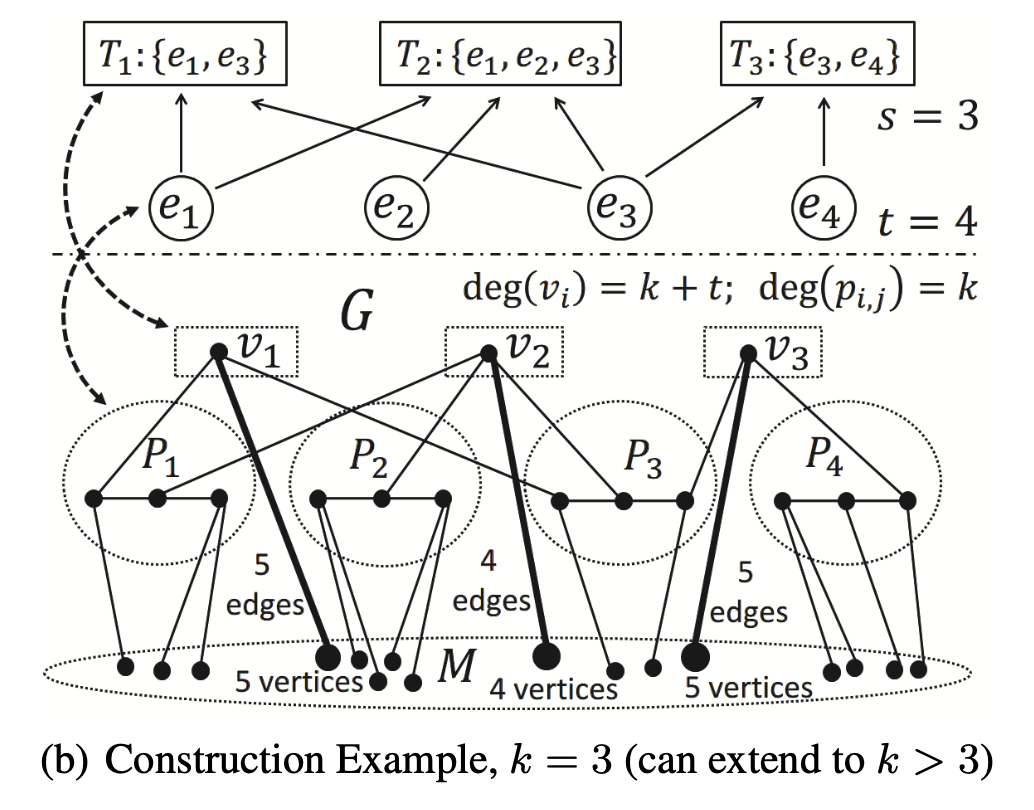
• Reduce Collapsed k-core Problem to Maximum Coverage Problem
• Maximum Coverage Problem
  • Finding at most $b$ sets to cover the largest number of elements, where $b$ is a given budget
• Reduction
  • Instance of maximum coverage problem with $s$ sets $T_1,\dots,T_s$ and $t$ elements $\{e_1,\dots,e_t\}=\cup _{1 \leq i \leq s}T_i$
  • The set of vertices in $G$ consists of $M,V,P$
    • $M$ consists of $(t+s)^4$ vertices in which every pair of vertices in $M$ are adjacent
    • $V$ consists of $s$ vertices, each vertex $v_i$ corresponds to the set $T_i$
      For each vertex $v_i$, add $k+t-|T_i|$ edges from $v_i$ to $k+t-|T_i|$ unique vertices in $M$
      • Maximum Coverage 의 원소 $e_j$ 를 하나의 정점 $v_j$ 로 대응
      • $m_i$ 제거의 결과로 차수가 $k$ 미만이 되면, follower 로 간주되어 k-core 에서 탈락
    • $P$ consists of $t$ parts, each part $P_i$ corresponds to the element $e_i$ and $P_i$ consists of $s$ vertices
      • For each $P_i$ add $s-1$ edges, for each $1\leq j < s$ and each element $e_j$
      • Add edge from $p_{i,j}$ to $p_{i,j+1}$
      • For each set $T_i$ and each element $e_j$, if $e_j \in T_i$, add an edge $(v_i, p_{j,i})$
  • Key idea
    - Follower 수는 $V$ 로만 계산하면 됨
    - $M$ 은 제거되지 않음, 구조 유지
    - 모든 $P_i$ 는 동일한 사이즈 유지
    - $v_i$ 제거하면 연결된 특정 $P_j$ 가 함께 삭제
    

---

Theorem 2. Let $f(A)=|F(A)|$. We have $f$ is monotone but not submodular for any $k$

Monotonicity

• $\text{if } A \sube A' \text{, then } f(A) \leq f(A')$
• $\text{if } A \sube A'$, $A'$ removes more vertices than $A$
• Thus $f(A') \geq f(A)$ and $f$ is monotone

Submodularity

• For two arbitrary collapsers sets $A$ and $B$, $f(A\cup B)+f(A\cap B) \leq f(A) + f(B)$

---

Solution

Motivation

• A straightforward solution is to enumerate all possible set $A$ with size $b$
  Time complexity of $O(\begin{pmatrix} n \\ b \end{pmatrix} m)$ is cost-prohibitive
• We only need to consider the vertices in $C_k(G_A)$ since all other vertices will be deleted by degree constraint
• Thus, a greedy algorithm is $O(bnm)$, $n$ and $m$ correspond to the number of candidate collapsers in each iteration and the cost of follower computation
• The number of vertices in $C_k(G_A)$ at Line 3 is considerably large

---

Reducing Candidate Collapsers

Two pruning rules to find the vertex with the largest number of followers

• Only vertices with degree $k$ in k-core and their neighbors in k-core can have followers
• $P$ denotes the vertices in k-core of $G$ with degree $k$
• $T$ : $C_k$ 에 있고 이웃 중 적어도 하나가 $P$ 에 속한 정점들

Theorem 3. Given a graph and the set $P$, if a collapsed vertex $x$ has at least one follower, $x$ is from $T$

• $P$ : 차수가 $k$ 인 vertices set
• $T$ : $C_k$ 에 있고 이웃 중 적어도 하나가 $P$ 에 속한 정점들
• Proof
  • If $x \in G \backslash C_k(G)$, x will be deleted in k-core computation, $|F(x)|=0$
  • If $x \in C_k(G) \backslash T$, $x$ survived in k-core computation and for each $x$'s neighbor $u$ within $C_k(G)$, $deg(u, C_k(G)) > k$ since $x\notin T$

---

Theorem 4. Given two vertices $x$ and $u$ in graph, we have $F(u) \sub F(x)$ if $u \in F(x)$

• Every vertex which is a follower of a vertex can be excluded from candidate collapsers
• A vertex with more neighbors in the set $P$ is more promising because all its neighbors in $P$ will follow the vertex to be deleted

---

CKC Algorithm

• To avoid the re-computation of $P$ and $T$ in the following iterations,
  update two sets at the end of each iteration
• $P$
  • $P_1$: vertices whose degrees are decreased to $k$ during the computation
  • $P_2$: vertices which are discarded during the computation
  • $P=P \cup (P_1 \backslash P_2)$
• $T$
  • Include new vertices in $NB(P_1)$
  • Delete vertices in $NB(P_2)$
• Order the candidates by their number of neighbors in $P$ in each iteration to prune more candidate collapsers

---

Evaluation

Effectiveness

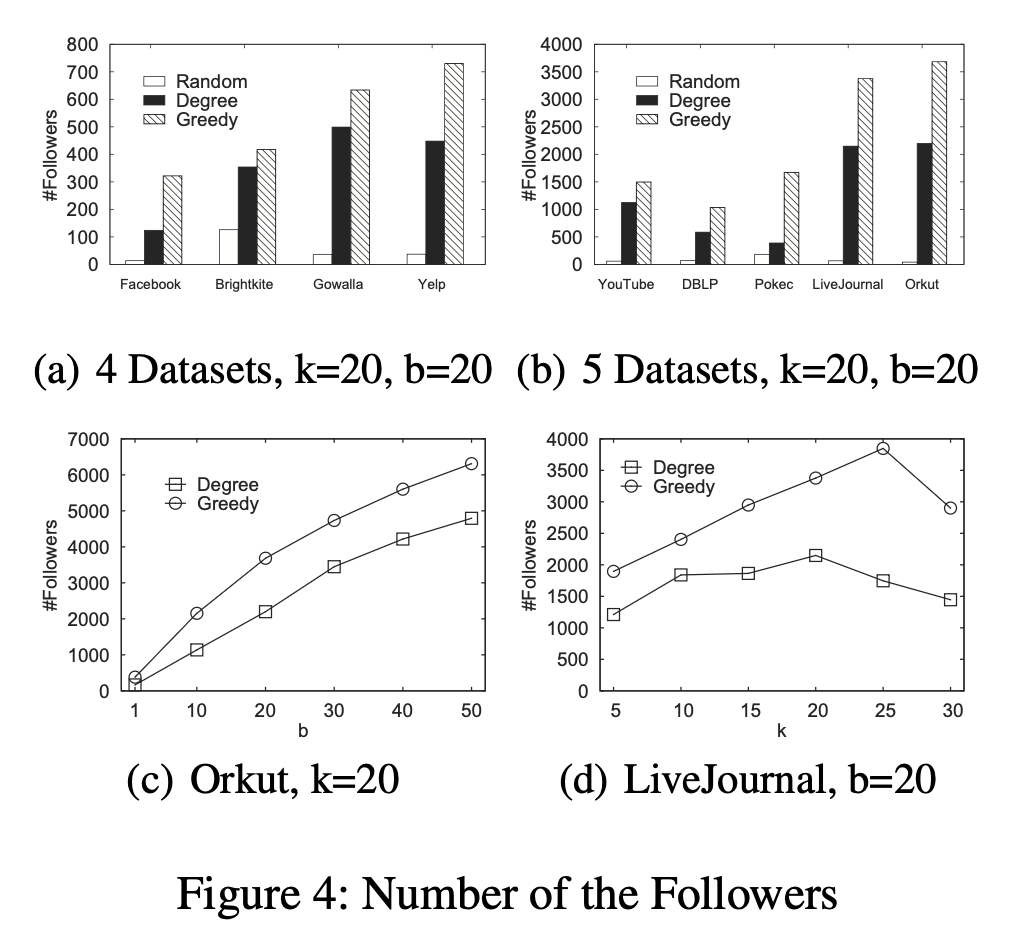
Baseline

• Random
  • Randomly chooose collapsers in k-core
• Degree
  • Choose collapsers in the candidate set $T$ with the largest degrees

Analysis

• Degree based approach is outperformed by CKC with a big margin
  • This Implies that it is not effective to find collapsers simply based on degree information

---

Efficiency

Evaluation of Individual Techniques

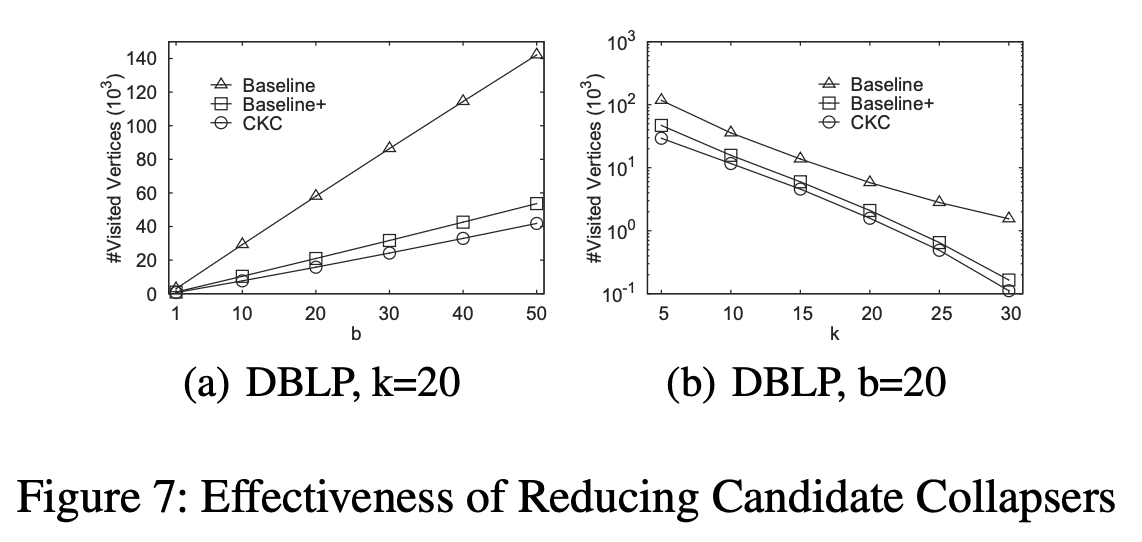
• Baseline+ represents Baseline equipped with Theorem 3
• Theorem 3, 4 reduces the number of candidate collapsers

Performance Evaluation

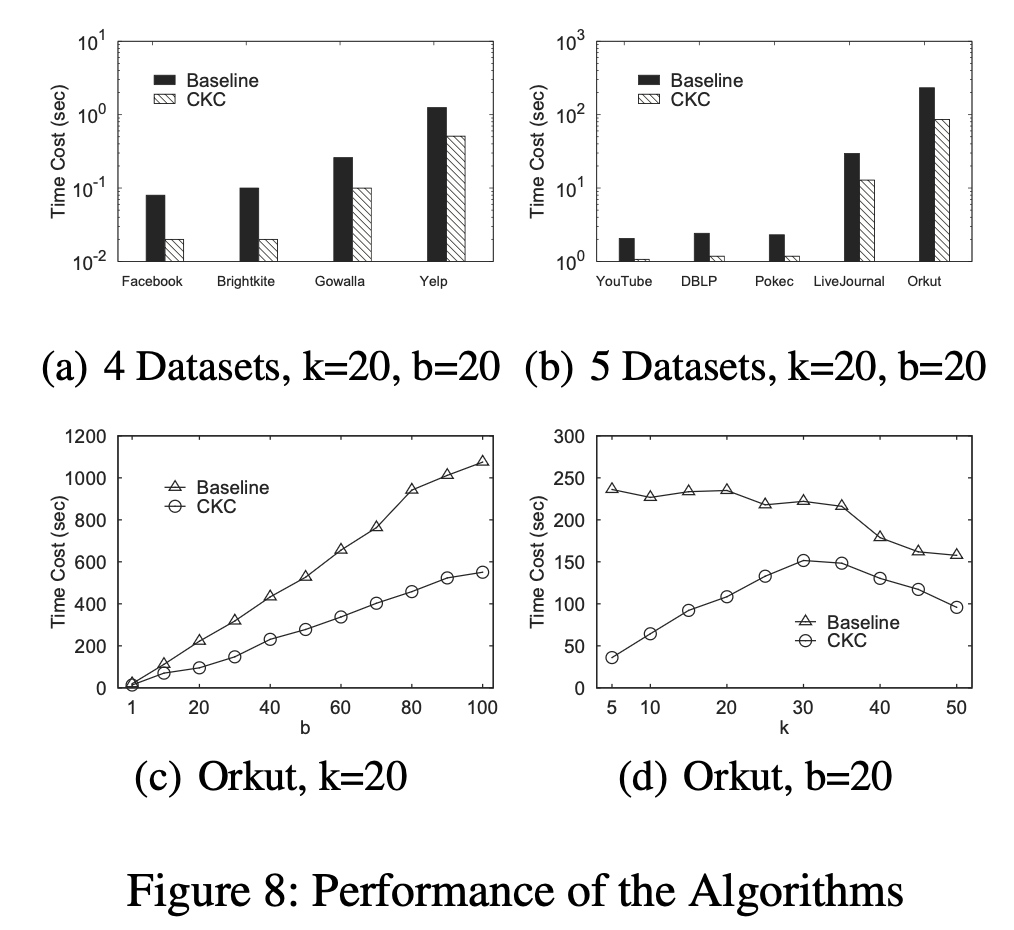
• (a) and (b)
  • CKC is scalable to the growth of the network size
• (c) and (d)
  • CKC is scalable to the different $k$ and $b$