[information theory] Entropy 정리

정보량 self informaion

$I\left(x\right)=-\log _2p\left(x\right)$

"놀람의 정도, degree of surprise"
"한 개의 사건에 대한 정보량"이다.

일어날 가능성이 높은 사건 보다 일어나기 일어날 가능성이 낮은 사건의 정보량이 더 높다.
예를 들면 내일 아침에 해가 뜰것이라는 사건보다 내일은 개기일식이 있을 사건이 더 많은 정보량을 가진다고 할 수 있다.

이를 수식적으로 표현하면 $I\left(x\right)=-\log _2p\left(x\right)$ 이다.

확률이 낮을 수록 정보량이 높은 반비례 관계를 표현하기 위해 -를 취하고 사건이 독립적이면 곱할 수 있는 성질을 활용하기 위해 log를 취한다.

Entropy

$H\left(x\right)=-\sum _{\ x}^{\ }p\left(x\right)\log _2p\left(x\right)$

"모든 사건 정보량의 기대값"

전체 사건 확률분포에 대한 불확실성의 양을 나타낼 때 쓰인다.
균일분포일수록 엔트로피 H(x)가 높고, 비균일분포일수록 H(x)가 낮음을 의미한다.
ex) 영어 문장을 전송할 때 필요한 bit수는 ? == Entropy

KL divergence

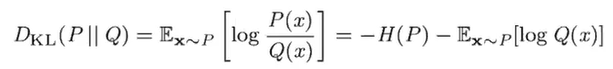
두 개의 확률 분포가 얼마나 다른지를 나타낸다.
ex) 영어로 한글 문장을 전송할 때 영어 문장을 전송할 때 보다 얼만큼의 bit를 추가해야하는가?

Cross Entropy

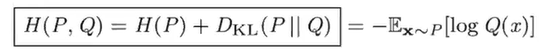
ex) 영어로 한글 문장을 전송할 때 필요한 총 bit수