PCA에 들어가기 앞서 우선 내적의 개념에 대해 짚고 넘어가자
내적
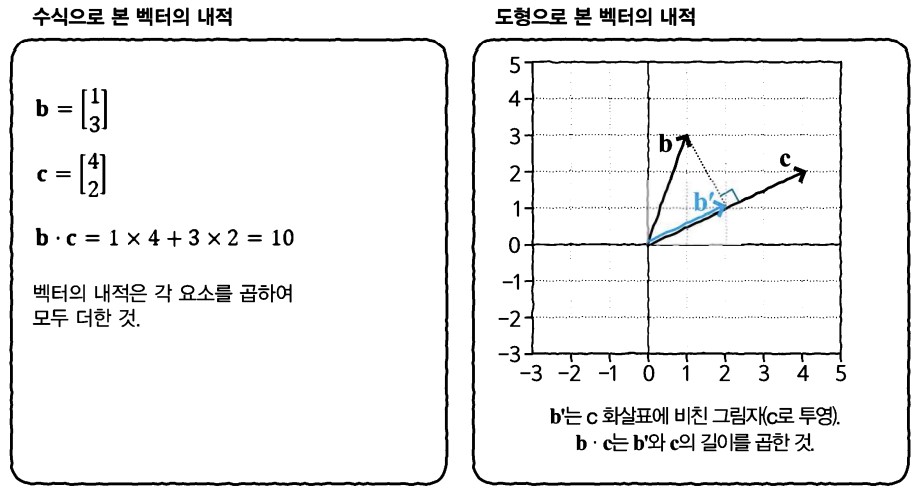
b를 c로 투영한 벡터럴 b'로 하여 b'와 c의 길이를 곱한 것으로 표현할 수 있고
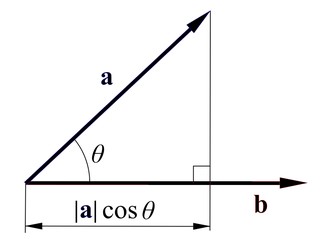
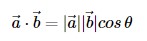
으로도 표현할 수 있다.
내적이 큰 값을 가질 때는 두 벡터가 비슷한 방향을 나타낼 때
내적이 작은 값을 가질 때는 두 벡터가 수직에 가까울 때 입니다.
즉 내적은 두 벡터의 방향의 유사성과 관련이 있습니다.
예를 들어 국어와 수학의 종합 점수를 얻을 때, 5:5의 비율 혹은 6:4의 비율로 종합 점수를 얻는 방식은 수학적으로는 점수 벡터를 특정 비율을 표현하는 벡터에 내적(즉, 기하학적으로는 정사영) 하는 문제로 환원해 생각할 수 있다.
그러면 데이터 벡터를 어떤 벡터에 내적(혹은 정사영)하는 것이 최적의 결과를 내주는가?
-> 이 문제에 대한 해결은 바로 공분산 행렬의 고윳값과 고유 벡터를 구함으로써 가능하다.
공분산 행렬
데이터의 구조를 설명, 특히 특징 쌍들이 얼마만큼이나 함께 변하는가를 나타낸 행렬이다.
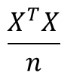
위와 같은 식으로 구하며
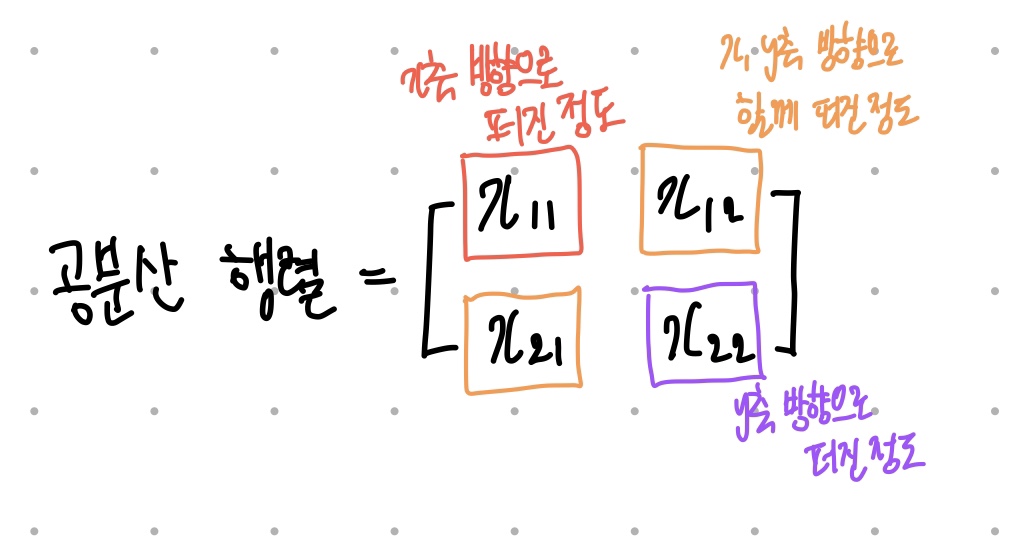
을 나타낸다.
공분산 행렬의 고유벡터는 그 행렬이 벡터에 작용하는 주축의 방향을 나타내고 (데이터가 어떤 방향으로 분산되어 있는지를 나타내준다고 할 수 있다.)
고유 값은 고유벡터 방향으로 얼마만큼의 크기를 가지는지를 나타낸다.
따라서 PCA(주성분 분석)은 데이터의 공분산 행렬의 고유벡터를 구하고 데이터들을 그 고유벡터에 정사영 시켜 차원을 낮추는 것이다.
참고 자료 및 그림 출처: 파이썬으로 배우는 머신러닝의 교과서, https://wikidocs.net/22384
