[알고리즘] 탐욕법(그리디) 알고리즘

mallin·2022년 2월 23일

알고리즘

목록 보기

7/9

🤑 탐욕법(그리디) 알고리즘

현재 상황에서 지금 당장 좋은 것만 고르는 방법으로 탐욕적으로 문제를 푸는 알고리즘

네이버에 greedy 에 대해서 찾아보면 뜻이 탐욕스러운, 욕심 많은 이라고 나오게 됩니다. 욕심많은 알고리즘 ? 이게 뭐야 ? 라고 생각할 수 있습니다.
그리디 알고리즘은 이름에서 알 수 있듯 단순 무식하게, 탐욕적으로 문제를 푸는 알고리즘입니다. 보통의 알고리즘 책에서는 탐욕법이라고 소개합니다.

여기서 탐욕적이라는 말은 '현재 상황에서 지금 당장 좋은 것만 고르는 방법'을 의미합니다. 그리디 알고리즘을 이용하면 매 순간 가장 좋아보이는 것을 선택하며, 현재의 선택이 나중에 미칠 영향에 대해서는 고려하지 않습니다.

그리디 알고리즘은 기준에 따라 좋은 것을 선택하는 알고리즘이기 때문에 문제에서 '가장 큰 순서대로', '가장 작은 순서대로'와 같은 기준을 알게 모르게 제시해줍니다.

당장 좋은 것(최선의 선택) 이란 ?

탐욕적이라는 말을 풀이하면서 당장 좋을 것만 고르는 방법이라고 나오는데요. 그렇다고 하면 여기서 당장 좋은 것은 무슨 의미일까요 ?

아래와 같은 트리가 있을 때, 시작점에서 시작하여 가장 큰 값을 구해야 한다고 가정하겠습니다.

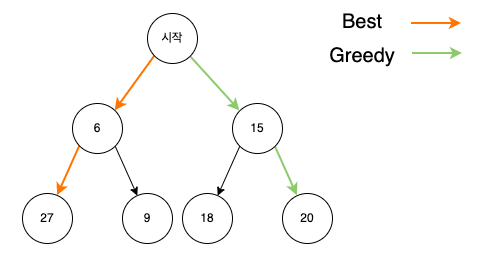
가장 Best 방법은 6 -> 27 로 가장 큰 값인 27을 구하는거지만
그리디 알고리즘 같은 경우는 현재 상황에서 지금 당장 좋은 것만 고르기 때문에 15 -> 20 로 가게 됩니다 .

즉 당장 좋은 것을 고르는 건 전체를 보지 않고, 지금 당장 닥친 상황만 보고 고르는거다. 라고 생각하시면 됩니다.

해결하는 방법

그리디 알고리즘을 사용해서 문제를 해결하기 위한 방법은 다음과 같습니다.

선택 절차 (Selection Procedure): 현재 상태에서의 최적의 해답을 선택합니다.
적절성 검사 (Feasibility Check): 선택된 해가 문제의 조건을 만족하는지 검사합니다.
해답 검사 (Solution Check): 원래의 문제가 해결되었는지 검사하고, 해결되지 않았다면 선택 절차로 돌아가 위의 과정을 반복합니다.

적용시 성립되어야 할 조건들

그리디 알고리즘을 적용하는 경우 2개의 조건이 성립되어야만 합니다.

탐욕적 선택 속성 (Greedy Choice Property) : 앞의 선택이 이후의 선택에 영향을 주지 않는다.
최적 부분 구조 (Optimal Substructure) : 문제에 대한 최종 해결 방법은 부분 문제에 대한 최적 문제 해결 방법으로 구성된다.

이러한 조건이 성립하지 않는 경우에는 탐욕 알고리즘은 최적해를 구하지 못합니다. 하지만, 이러한 경우에도 탐욕 알고리즘은 근사 알고리즘으로 사용이 가능할 수 있으며, 대부분의 경우 계산 속도가 빠르기 때문에 실용적으로 사용할 수 있습니다.

근사 알고리즘이란 ?

어떤 최적화 문제에 대한 해의 근사값을 구하는 알고리즘을 의미합니다.
가장 최적화되는 답을 구할 수는 없지만, 비교적 빠른 시간에 계산이 가능하며 어느 정도 보장된 근사해를 계산할 수 있습니다.

💸 거스름돈 문제

❓ 당신은 편의점 알바생이다. 카운터에는 1000원, 500원, 100원, 50원, 10원이 무한이 존재한다고 가정한다. 손님에게 거슬러 줘야 할 돈이 N원일 때 거슬러 줘야 할 돈의 최소 개수를 구하라. 단, 거슬러 줘야 할 돈 N 은 항상 10의 배수다.

이 문제는 그리디 알고리즘을 이용해 풀 수 있는 대표적인 문제입니다.
간단한 아이디어만 떠올리면 쉽게 풀 수 있는데, 바로 '가장 큰 화폐 단위부터' 돈을 거슬러 주는 것입니다.

만약 N 이 5670 원이라고 했을 때

금액	거슬러 주는 액수	남은 금액
1000원	5670/1000 = 5장	5670 - 5000 = 670원
500원	670/500 = 1개	670 - 500 = 170원
100원	170/100 = 1개	170 - 100 = 70원
50원	70/50 = 1개	70 - 50 = 20원
10원	20/10 = 2개	20 - 20 = 0원

로 거슬러 줄 수 있고, N이 5670원일 때 손님이 받는 최소 개수는 10개입니다.

탐욕 알고리즘의 해결 방법을 적용한다고 했을 때
1. 선택 절차
     👉 거슬러 줘야 할 돈의 개수를 줄이기 위해 현재 가장 비싼 돈을 선택한다. (1000원)
2. 적절성 검사
     👉 1번 절차로 선택된 돈이 남은 거스름돈을 넘는지 확인하고, 넘는다면 1번 절차로 다시 돌아가서 돈의 액수를 줄인다.
3. 해답 검사
     👉 거슬러줘야 할 거스름돈이 남은지 확인하고 남은 경우 1번 절차로 돌아간다.

해당 프로그램을 자바로 작성했을 때 코드는 다음과 같습니다.

int n = 5670;
int count = 0;
        
int money_type[] = {1000, 500, 100, 50, 10};
        
for(int money:money_type) {
	count += n / money;
	n %= money;
}
        
System.out.println(count);

코드를 보면 화폐의 종류만큼 반복을 수행해야하는데 따라서 화폐의 종류가 K개라고 할 때 위 소스 코드의 시간 복잡도는 O(K)가 됩니다.

그리디 알고리즘의 정당성

그리디 알고리즘으로 문제의 해법을 찾았을 때는 그 해법이 정당한지 검토해야 합니다.
거스름돈 문제를 그리디 알고리즘으로 해결할 수 있는 이유는 가지고 있는 동전 중에서 큰 단위가 항상 작은 단위의 배수이므로 작은 단위의 동전들을 종합해 다른 해가 나올 수 없기 때문입니다

예를 들어서, 800원을 거슬러 줘야 하는데 화폐 단위가 500원, 400원, 100원일 때 그리디 알고리즘으로는 4개의 동전(500+100+100+100)을 거슬러줘야 한다고 나오는데 최적의 해는 2개의 동전(400+400)을 거슬러 주는 것입니다.

👉 그렇기 때문에 그리디 알고리즘 문제에서는 문제 풀이를 위한 최소한의 알고리즘을 떠올리고 이것이 정당한지 검토할 수 있어야 답을 도출할 수 있습니다.