최대공약수 (GCD, Greatest Common Divisor)
두 자연수의 공통된 약수 중 가장 큰 수
예를 들어서 10과 14가 있을 때
10의 약수 = 1,2,5,10
14의 약수 = 1,2,7,14
공통되는 약수 = 1,2 인데 둘 중 큰 수는 2 이기 때문에
10과 14의 최대공약수는 2가 됩니다.
Brute force (무차별 대입) 로 구하는 방법
Brute force 방식은 두 수 중 작은 수를 선택한 다음 1부터 작은 자연수까지의 모든 수로 두 수를 나누면서 동시에 나누어 떨어지는 가장 큰 수를 구하는 방법입니다.
#include <stdio.h>
#include <iostream>
using namespace std;
int main() {
int a = 9, b = 15;
int min_num = (a < b ? a : b);
for (int i=min_num; i>0; i--) {
if (a % i == 0 && b % i == 0) {
cout << i;
break;
}
}
return 0;
}시간복잡도는 O(N) 입니다.
유클리드 호제법을 사용해서 구하는 방법
유클리드 호제법은 x, y 의 최대공약수는 y, r 의 최대공약수와 같다는 원리를 이용하는 것입니다.
즉, 계속해서 x 값에는 y 값을 대입하고 y 값에는 r 값을 대입하다보면 언젠가는 r 이 0 이 되는데 이때에 y 값에 있는 값이 최대공약수 입니다.
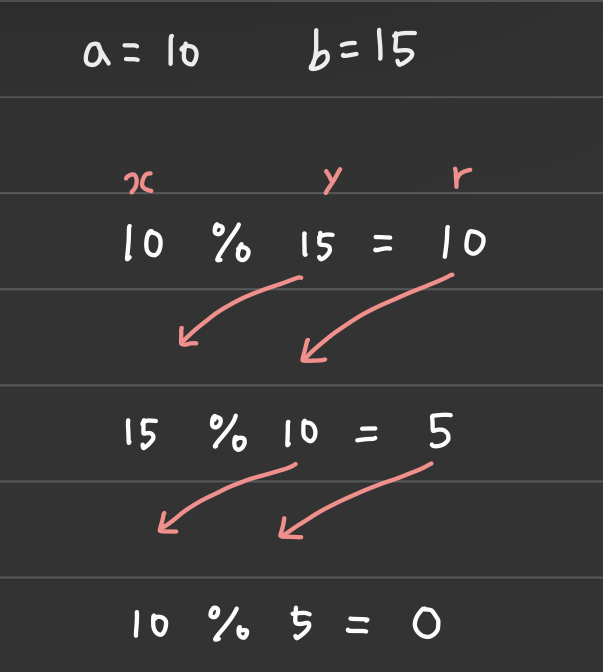
위처럼 10과 15가 있을 때 계속적으로 대입하고 나누다보면 y 가 5일 때 r 이 0이 되기때문에 최대공약수는 5가 됩니다.
수식으로 나타냈을 때에는 다음과 같습니다.
GCD(A, B) = GCD(B, A%B)
if A%B = 0 -> GCD = B
else GCD(B, A%B) 재귀 함수
#include <stdio.h>
#include <iostream>
using namespace std;
int gcd(int a, int b) {
if (b == 0) return a;
else return gcd(b, a % b);
}
int main() {
int a = 12, b = 18;
cout << gcd(a,b);
return 0;
}반복문 사용
#include <stdio.h>
#include <iostream>
using namespace std;
int main() {
int a = 12, b = 18, r = 1;
while(a % b != 0) {
r = a % b;
a = b;
b = r;
}
cout << b;
return 0;
}
최소공배수 (LCM)
두 자연수의 공통된 배수 중 가장 작은 수
예를 들어서 6과 9가 있을 때
6의 배수 = 6, 12, 18, 24, 30, 36 ...
9의 배수 = 9, 18, 27, 36, 45, 54 ...
공통되는 배수 = 36 ... 인데 가장 작은 수는 36이기 때문에
6과 9의 최소공배수는 36이 됩니다.
공식 사용하기
최소공배수는 두 자연수의 곱 / 최대 공약수 라는 공식으로 구할 수 있습니다.
#include <stdio.h>
#include <iostream>
using namespace std;
int gcd(int a, int b) {
if (b == 0) return a;
else return gcd(b, a % b);
}
int main() {
int a = 12, b = 18;
cout << a * b / gcd(a,b);
return 0;
}백준 문제
2609번 최대공약수와 최소공배수
11690번 LCM(1, 2, ..., n)
14860번 GCD 곱
🙇🏻♀️ 레퍼런스
최대공약수(GCD), 최소공배수(LCM) 구하기 유클리드 호제법 알고리즘 :: 코드자몽
최대 공약수(GCD) 알고리즘 - 유클리드 호제법
[Python] 최소공배수, 최대공약수란? 파이썬 알고리즘으로 쉽게 구현하기 / for문, 유클리드 호제법 이용


6의 배수 = 6, 12, 18, 24, 30, 36 ...
9의 배수 = 9, 18, 27, 36, 45, 54 ...
공통되는 배수 = 36 ... 인데 가장 작은 수는 36이기 때문에
6과 9의 최소공배수는 36이 됩니다.
위 문장에서 공통되는 배수가 잘못된 듯 합니다~!
가장 작은 수는 18 인 듯해요 ㅎㅎ