한 번 계산한 문제는 다시 계산하지 않도록 하는 알고리즘
👩 : DP ? 그 정해인하고 구교환 하고 나온 그 드라마 ? 아 그거 재밌게 봤지 ~
아 아뇨 그 DP 가 아니고 이 DP 는 동적 계획법(Dynamic Programming) 이라는 알고리즘 입니다
1. 동적 계획법 (DP) 란 ?
큰 문제를 작은 문제로 나누어서 푸는 방법
이름만 봤을 때 동적 으로 작동하거나 계획적으로 작동하는 부분이 있나 ? 싶을 수 있는데 Richard Bellman이 1950년대에 사용한 단어로 그냥 멋있어서 이렇게 이름을 지었다고 한다 (인생은 Richard Bellman 처럼)
2. DP 사용 이유
그러면 DP 를 사용하는 이유는 뭘까 ?
알고리즘을 풀 때 보통 재귀를 사용해서 푸는데, 재귀의 경우에는 같은 로직을 여러번 반복하기 때문에 비효율적 계산 이 될 확률이 굉장히 높아진다.
재귀를 사용한 문제 중 가장 유명한 피보나치 수열을 예로 보자.
그전에 혹시라도 피보나치 수열이 뭔지 모르는 사람이 있을지도 모르니 잠깐 짚고 넘어가자면,
피보나치 수열은 첫번째 및 두번째 항이 1이며 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열이다.
이걸 숫자로 나타내보면
1 1 2 3 5 8 13 21 ...으로 나타낼 수 있다
그럼 이걸 재귀 코드로 구현해보자
int fibo(int n){
if (n<=2) return 1;
return fibo(n-1) + fibo(n-2);
}그러면 위와 같은 코드로 나타낼 수 있는데, 첫번째와 두번째 항은 1이기 때문에 n 이 2 보다 작거나 같은 경우에는 1을 리턴해주고, 바로 앞 두 항의 합인 값을 수해야 하기 때문에 fibo(n-1) + fino(n-2) 를 return 해준다.
5번째 피보나치 수열의 값을 구한다고 했을 때 다음과 같이 실행된다.
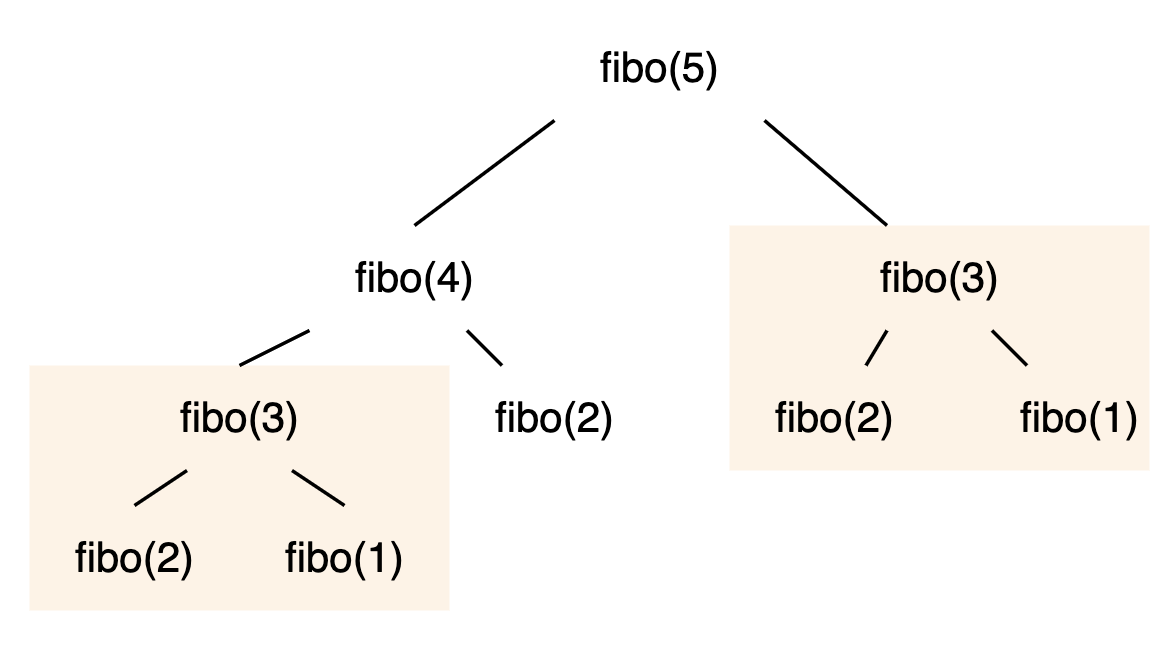
뭔가 이상한데 🤔
왼쪽 아래 있는 fibo(3) 과 오른쪽에 있는 fibo(3) 이 작동하는게 완전 동일하다 !!!!!
그렇게 되면 연산이 두 번 진행되게 되고, 지금은 fibo(5) 라서 반복적으로 작동하는 코드가 별로 없지만 . . . . . 값이 커지면 커질 수록 중복되는 로직이 많아 질 수 밖에 없다.
바로 이럴 때 DP 를 사용하면 효율적으로 문제를 해결 할 수 있다 ‼️
3. DP 사용 조건
DP 에는 두가지 사용 조건이 있다.
첫번째, 큰 문제를 작은 문제로 나눌 수 있는 경우
두번째, 작은 문제에서 구한 정답이 그것을 포함하는 큰 문제에서도 동일한 경우
A --(`AX[1km], AX1[5km], AX2[8km]`)-> X --(`XB[1km], XB1[5km], XB2[8km]`)-> B 라고 했을 때 A 에서 X 로 가는 최단의 방법은 AX,
X 에서 B 로 가는 최단의 방법은 XB 이고, 전체 최단의 경로도 AX - XB 가 되게 된다.
만약 다른 경로를 선택한다고 해도 전체 최단 경로는 변하지 않는다. 이처럼 부분 문제에서 구한 최적 결과가 전체 문제에서도 동일하게 적용되어 결과가 변하지 않을 때 DP 를 사용할 수 있다 !
4. 메모이제이션 (Memoization)
연산은 한번만 진행해야 한다.
메모이제이션은 DP 를 구현하는 방법 중 한가지 기법으로 한 번 구한 결과를 메모리에 저장해두고, 같은 식을 다시 호출하면 저장해둔 결과를 그대로 가져오는 기법을 의미한다.
동작 방식은 다음과 같다.
① 처음 진행되는 연산인 경우 기록
② 이미 진행된 연산인 경우 다시 값을 구하는게 아니라 기록된 값을 가져옴
그러면 메모이제이션을 사용해서 피보나치 수열을 구현해보자.
int data[100] = {0,};
int fibo(int n) {
if (n<=2) return 1;
if (data[n] == 0) data[n] = fibo(n-1) + fino(n-2);
return data[n];
}중복적으로 로직이 일어나지 않도록 data 배열에 재귀로 구한 값을 저장해두고 이미 있는 값 ( = 한번 수행된 값) 인 경우 다시 연산을 하지 않고 배열에서 꺼내서 사용한다.
이를 통해, 중복되는 연산이 사라질 수 있다.
나 같은 경우에는 DP 를 공부하면서 메모이제이션과 개념이 엄청 헷갈렸는데 간단하게 정리하자면
메모이제이션 = 이전에 계산된 결과를 일시적으로 기록해 놓는 넓은 개념이며, DP 를 구현하기 위한 기법 중 하나 ! 라고 생각하면 된다.
5. 구현 방법
① BOTTOM-UP
작은 문제부터 차례대로 푸는 방식. 반복문으로 구현
- 아래에서 부터 계산을 수행 하고 누적시켜서 전체 큰 문제를 해결하는 방식
- DP 의 전형적인 형태
- 결과 저장용 리스트를
DP 테이블이라고 한다.
과정
1. 문제를 크기가 작은 문제부터 차례대로 푼다.
2. 문제 크기를 조금씩 늘려가면서 푼다.
3. 반복해나가면서 큰 문제를 계속 풀어간다.
int bottomUp(int n) {
fiboData[0] = 0;
fiboData[1] = 1;
for (int i=2; i<=n; i++)
fiboData[i] = fiboData[i - 1] + fiboData[i - 2];
return fiboData[n];
}bottomUp(6) 을 호출하면 fiboData[2] 부터 차근 차근 데이터를 구한다
② TOP-DOWN
큰 문제를 작은 문제로 쪼개면서 푸는 방식. 재귀로 구현
- 위에서 부터 바로 호출을 시작하여 dp[0]의 상태까지 내려간 다음 해당 결과 값을 재귀를 통해 전이시켜 재활용하는 방식
- 메모이제이션은 TOP-DOWN 방식에 국한되어서 사용된다
과정
1. 큰 문제를 작은 문제로 나눈다
2. 작은 문제를 푼다
3. 푼 작은 문제를 바탕으로 큰 문제를 푼다
int topDown(int n) {
if (n<=2) return 1;
if (fiboData[n]==0) fiboData[n] = fibo(n-1) + fibo(n-2);
return fiboData[n];
}topDown(6) 을 호출하면 topDown(6) 부터 아래로 호출하되, 중복된 로직은 수행하지 않는다
함께 풀면 좋은 문제들
🙇🏻♀️ 레퍼런스
[자료구조와 알고리즘] 동적 계획법(Dynamic Programming, DP)
알고리즘 - Dynamic Programming(동적 계획법)
동적 계획법(Dynamic Programming)
.png)
