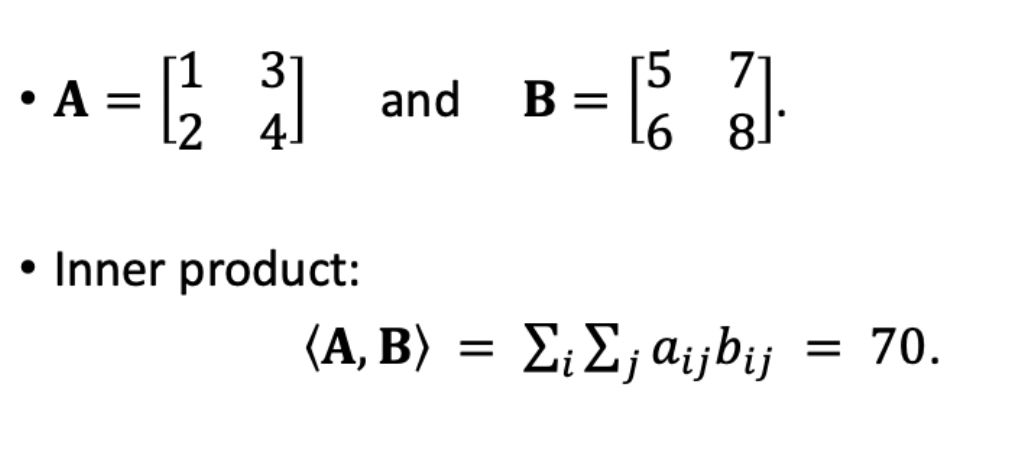위 reference 를 보며, CNN 개념에 대한 공부 기록용 포스팅입니다.
CNN 이란
CNN 은 Convolutional Neural Networks 의 약자로 Convolution 이라는 전처리 작업을 하는 Neural Network 모델이다.
CNN을 왜 사용할까
이는 DNN 의 문제점에서 출발한다.
일반 DNN은 기본적으로 1차원 형태의 데이터를 사용한다. 따라서 1028 x 1028 같은 2차원 형태의 이미지가 input 값이 될 경우, 이것을 flatten 시켜서 한 줄 데이터로 만들어야 한다.
이 과정에서 이미지의 공간적/지역적 정보 (spatial/topological information) 이 손실되게 된다. 또한 추상화과정 없이 바로 연산과정으로 넘어가 학습시간과 능률의 효율성이 저하된다.
이를 위한 해결책으로 CNN은 이미지를 raw input 그대로 받음으로써 spatial/topological information 을 유지 한 채 feature 들의 계층을 빌드업 한다.
CNN의 중요 포인트는 이미지 전체보다 부분을 보는 것, 그리고 이미지의 한 픽셀과 주변 픽셀들의 연관성을 살리는 것이다.
CNN 을 왜 사용하는지 아래 예시를 통해 더 쉽게 이해해보자.
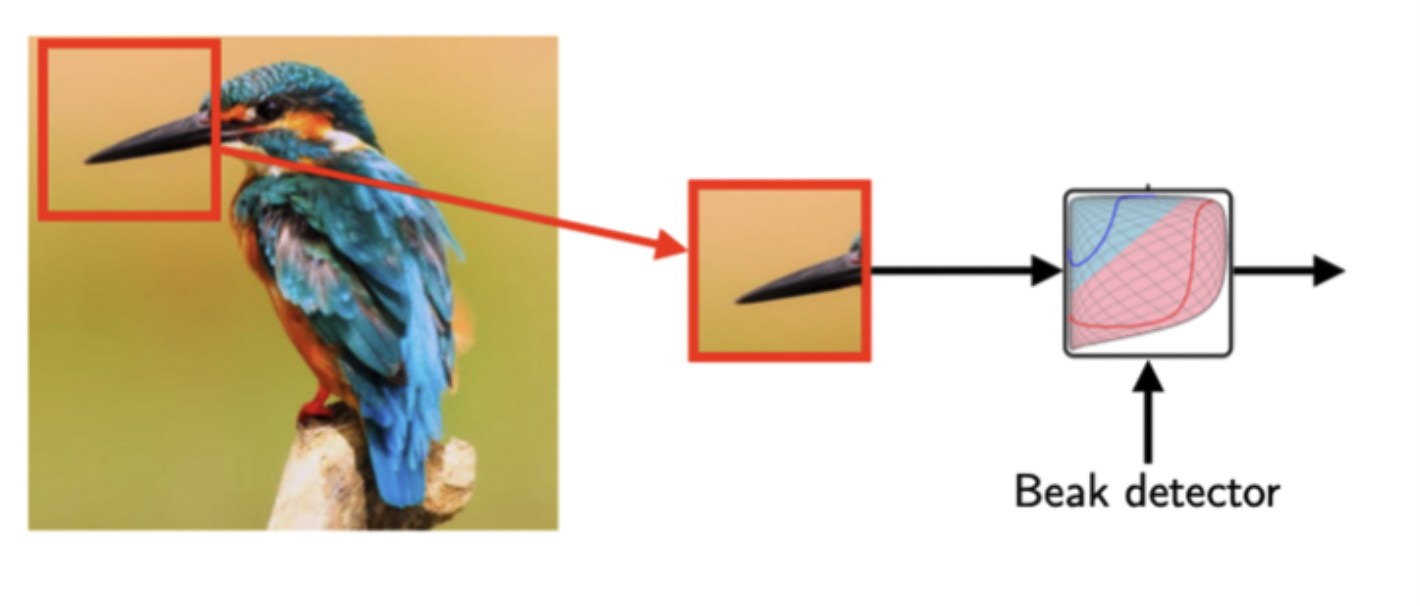
예시로 어떠한 이미지가 주어졌을 때 이것이 새의 이미지인지 아닌지 결정할 수 있는 모델을 만들려한다. 이때 새의 주요 특징인 새의 부리가 중요한 포인트가 될 수 있다. 따라서 모델이 주어진 이미지에 새의 부리 존재 유무를 판가름 하는 것이 중요 척도가 될 것이다.
하지만 전체 이미지에서 새의 부리는 비교적 작은 부분으로, 모델이 전체 이미지를 보는 것보다는 새의 부리 부분을 잘라 보는게 효율적이다.
이것을 해주는 것이 CNN 으로, CNN의 뉴런이 패턴(이 경우 새의 부리) 을 파악하기 위해 전체 이미지를 모두 다 볼 필요는 없는 것이다.
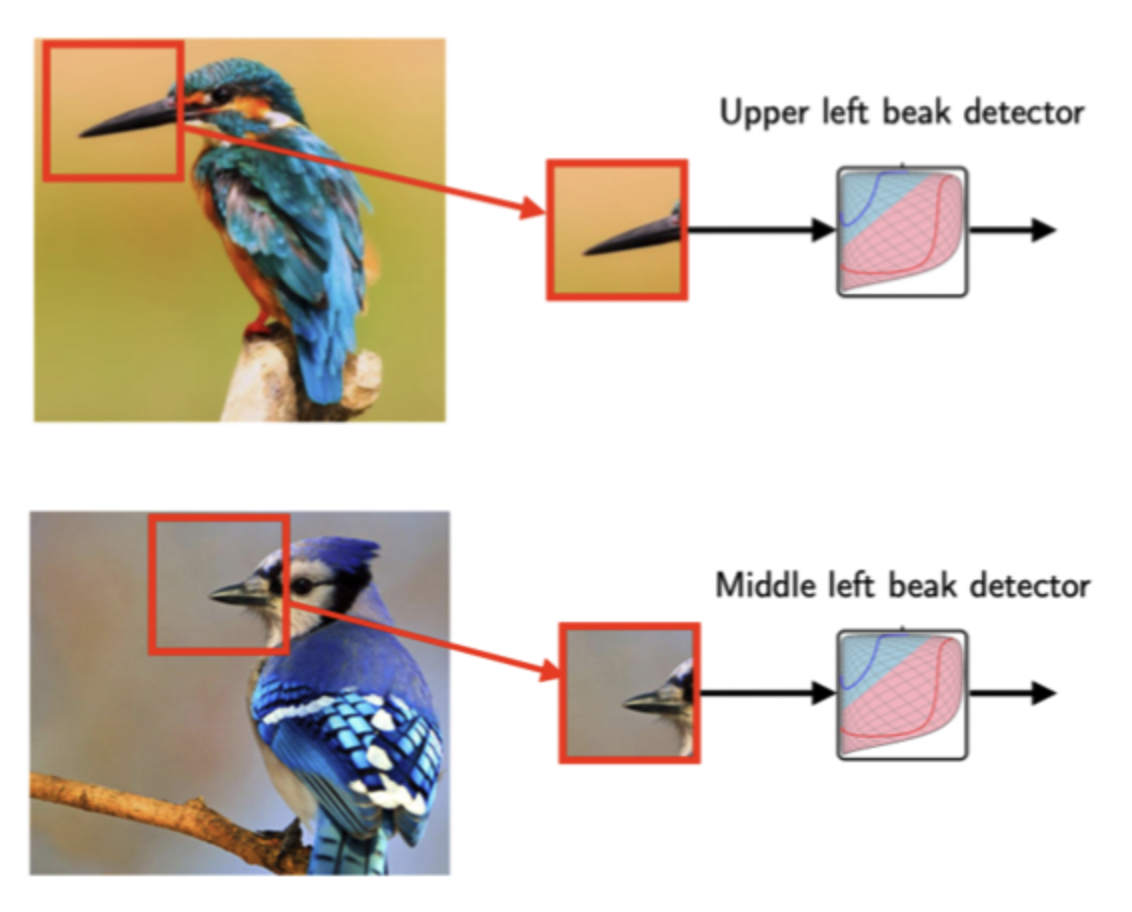
또한 위의 두 이미지를 보면 새의 부리부분이 이미지 속 다른 위치에 있다는 것을 알 수 있다. 왼쪽 상단, 가운데 상단에 각각 위치해 있는데, 이 때문에 전체 이미지를 보는 것 보다 이미지의 부분을 캐치하는 것이 중요하고 효율적이다.
MLP vs CNN
일반 신경망과 CNN을 비교하면 아래와 같다.
일반적인 신경망(MLP)을 이용해 이미지를 처리할 때는 매우 많은 가중치가 필요. MNIST 데이터셋을 넘어서 CIFAR-10 데이터셋만 되어도 MLP를 이용하면 해결하기 어려움. 32 x 32 크기의 색상 이미지라면 32 x 32 x 3 = 3,072개의 가중치(weight)가 필요.
은닉층의 크기가 1,000이라면 순식간에 3,072,000개의 파라미터가 필요하게 됨.
반면에 CNN은 커널(kernel)을 공유하기 때문에 훨씬 적은 가중치만 있어도 된다.
- 일반 신경망의 특징: 많은 가중치 필요, fully-connection 사용
- CNN의 특징: 적은 가중치 필요(파라미터 공유), 이미지 처리에 적합
예를 들어 컨볼루션 연산에서 커널의 개수 k = 12, 수용 영역 크기 F = 4, 이전 레이어의 채널 = 3 이라고 해보자.
그러면 실제로 커널에 필요한 파라미터의 개수는 12 x 4 x 4 x 3 = 576 이 된다.
이 처럼 커널을 이용해 파라미터를 공유하면 필요한 가중치의 개수가 획기적으로 줄어들게 된다. 이런 아이디어가 사용될 수 있는 이유는, 하나의 패치 특징(patch feature)은 이미지의 전반적인 위치에서 나타날 수 있기 때문이다.
예를 들어 일반적인 이미지 데이터셋을 확인해 보면 대각선 엣지(edge) 형태의 특징은 이미지 전반에 나올 수 있다.
CNN 주요 컨셉
Convolution 의 작동 원리

2차원의 이미지의 경우 위와 같이 픽셀 단위로 구성되어있다.
위의 이미지는 MNIST Dataset 의 샘플 중 하나로 손글씨 '8'의 gray scale 이미지로 28x28 단위의 픽셀로 구성되어 있다.
이 데이터의 input 으로 28x28 matrix 로 표현할 수 있다. 즉 2차원 이미지는 matrix로 표현할 수 있으며, CNN의 input 값으로 matrix로 표현된 이미지를 넣어준다.
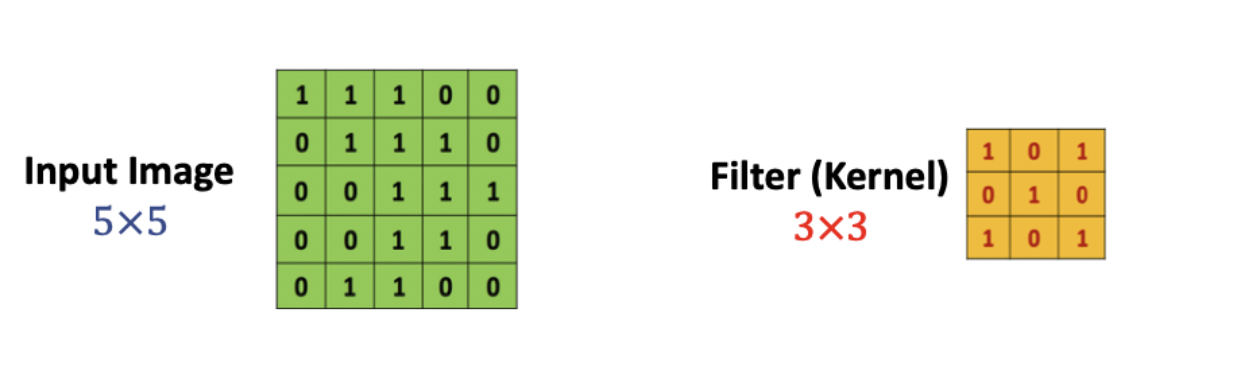
예를 들어, 5x5 matrix 이미지를 입력한다고 가정한다. CNN에는 필터(커널)이 존재한다(예시의 경우 3x3). convolution 연산은 쉽게 이 하나의 필터(커널)를 input image에 전체적으로 훑어주는 것이다.
즉 input image의 모든 영역에 같은 필터를 반복 적용해 패턴을 찾아 처리하는 것이 convolution 연산의 목적이다.
이렇듯 필터를 통해 연산처리를 해주는데, 이 연산처리는 matrix 와 matrix 간의 Inner Product 라는 것을 사용한다.
Inner Product
같은 크기의 두 matrix를 놓고 각 위치에 있는 숫자를 곱해 모두 더해주는 것
본론으로 돌아와 input image matrix 와 filter의 연산처리를 그림으로 살펴보면
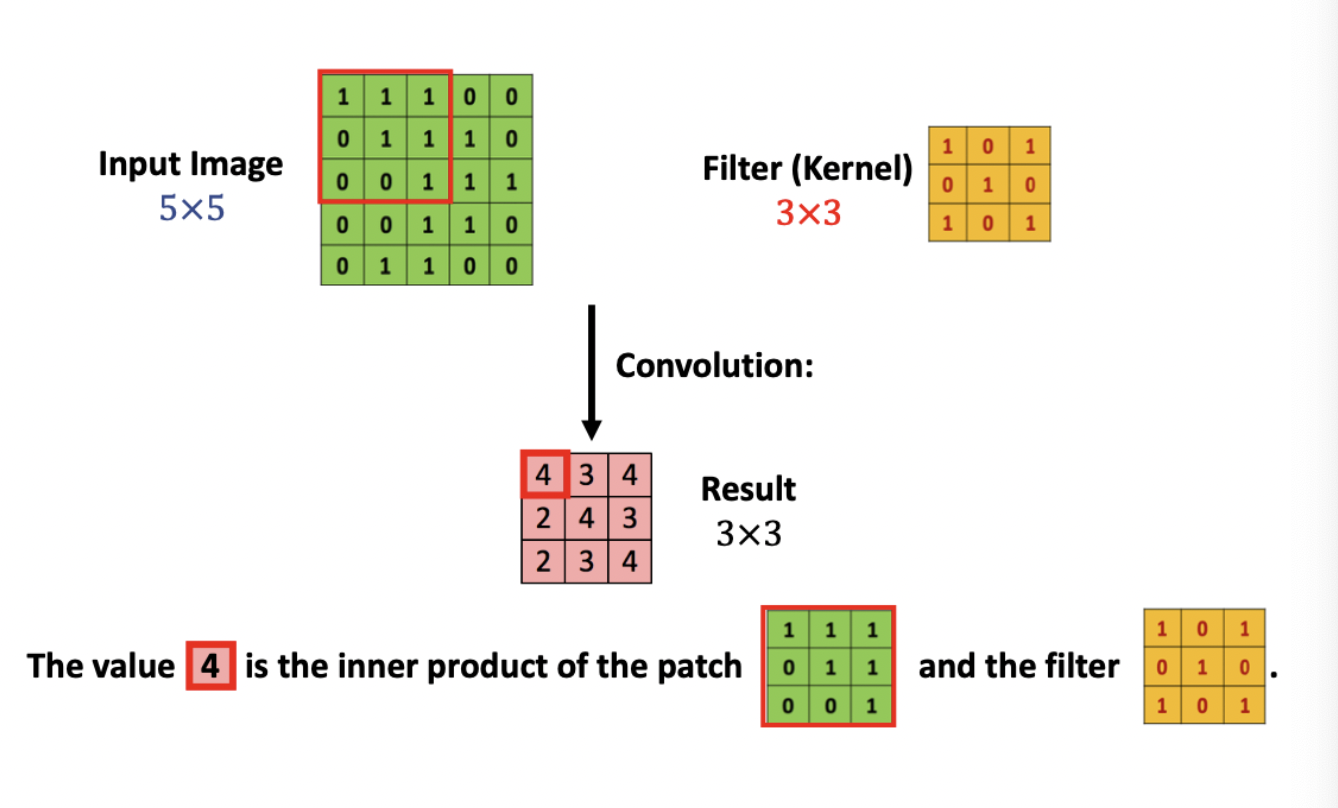
빨간 테두리 부분의 matrix 와 Filter 를 Inner product 연산을 하면, 그 결과값은 4가 나온다.
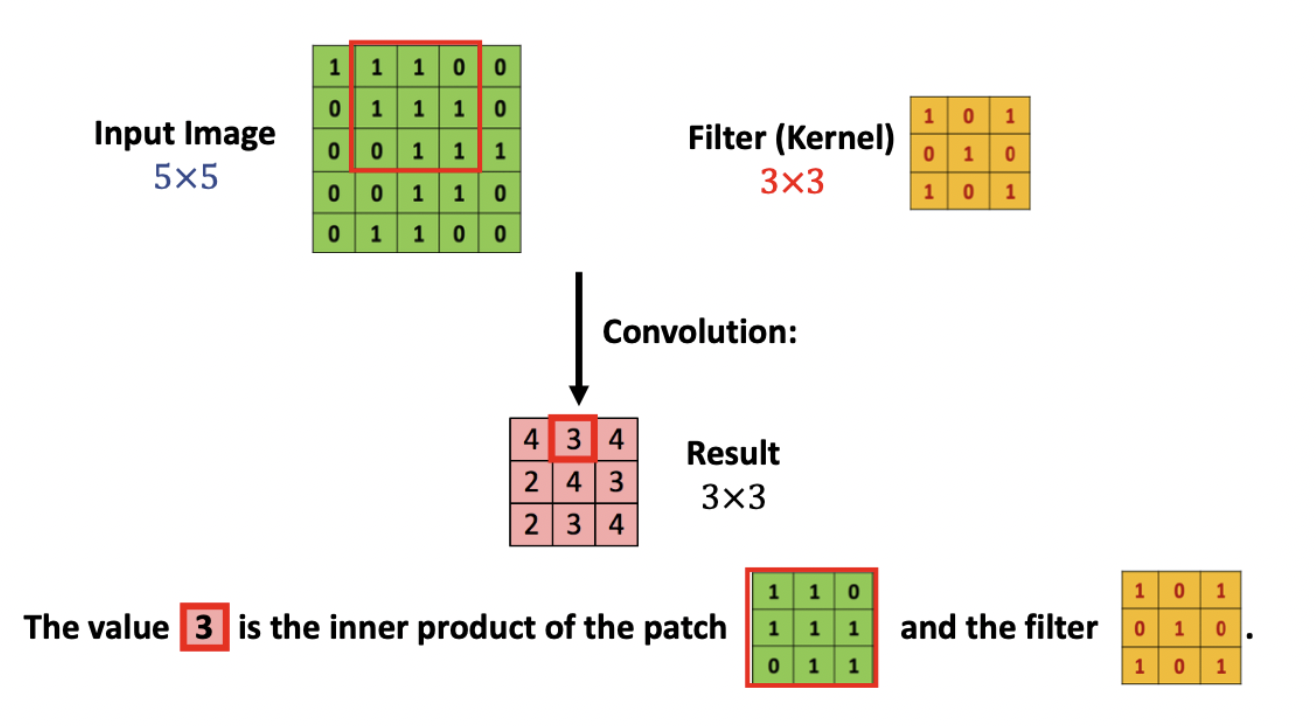
필터를 한 칸 옆으로 옮겨, 다음 빨간 테두리 부분의 matrix와 필터의 연산처리를 해주어 결과로 3을 얻는다.
이러한 과정을 반복하여 분홍색의 result matrix를 얻을 수 있다.
이때 result matrix의 dimension이 3x3 임을 알 수 있는데, 이는 input matrix의 dimension 보다 작다.
입력값 : d_1 x d_2
필터 : k_1 x k_2
결과값 : (d_1 - k_1 + 1) x (d_2 - k_2 + 1)Zero Padding
앞서 살펴 본 Convolution 연산을 통해 result dimension이 줄어듦을 확인했다. 이는 손실되는 부분이 발생한다는 뜻인데, 이를 방지하기 위해 Padding 이라는 방법을 사용할 수 있다. 쉽게 0으로 구성된 테두리를 이미지 가장자리에 감싸 주는 작업이다.
그렇다면 위의 경우 5 x 5 크기의 input image 가 7 x 7 크기가 될 것이다. -> (d_1 +2) x (d_2 +2)
이 상태에서 3 x 3 필터를 적용하면 기존 input dimenstion 과 동일한 5 x 5 와 같은 결과값을 얻을 수 있다. 이를 통해 손실을 방지할 수 있다.
Stride
stride 는 필터를 얼마만큼 움직여 주는가에 대한 값이다. stride 값이 1일 경우 필터를 한 칸씩 움직여 주는 것이다. (위의 예시의 경우 stride 값이 1)
stride 는 1이 기본값이고 1보다 큰 값이 될 수도 있다. stride 값이 커질 경우 필터가 이미지를 건너뛰는 칸이 커지기 때문에 result image의 크기는 작아진다.
입력값 : d_1 x d_2
필터 : k_1 x k_2
stride : 1
결과값 : (((d_1 - k_1) / s) + 1) x (((d_2 - k_2) / s) + 1)The Order-3 Tensor
지금까지 우리는 2차원 이미지의 입력값을 살펴보았다. 입력값이 3차원인, 컬러 이미지의 경우 R,G,B 의 세 가지 채널로 구성되어 d_1 x d_2 x d_3 과 같은 삼차원의 크기를 갖는다.
이러한 모양을 order-3 텐서라고 칭한다. 마찬가지로 2차원의 이미지는 order-2 텐서 (=matrix) 라고도 칭한다.
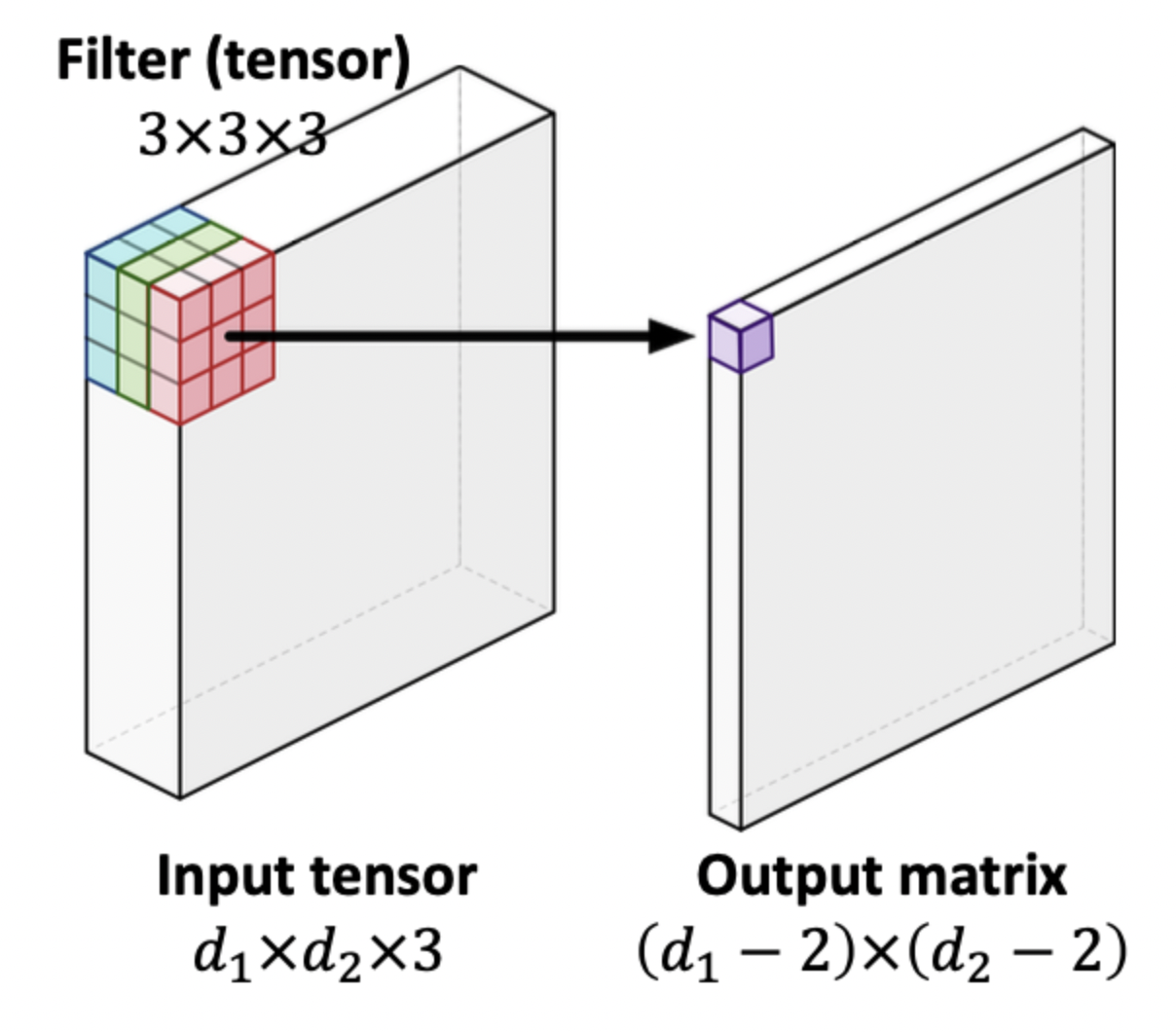
위의 이미지와 같이, 필터는 k1 x k2 x k3 의 크기를 가진 order-3 텐서가 된다. 연산처리는 똑같이 Inner product 를 사용한다. 당연히 결과값은 matrix 이다.
Convolution computation and dimension
커널을 이용해 컨볼루션 연산을 수행할 때 이전 레이어의 channel 크기와 커널의 channel 크기가 동일하다.
예를 들어 입력 크기가 32 x 32 x 3 이면, 커널에서도 5 x 5 x 3과 같이 채널의 크기로 3을 사용한다.
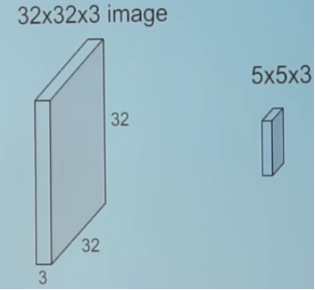
또한 컨볼루션 연산을 수행한 뒤에는 커널의 개수가 레이어의 채널 크기가 된다.
예를들어 32 x 32 x 3 입력에 대하여 5 x 5 x 3 짜리 커널을 6개 사용했다면, 출력으로 나온 레이어는 28 x 28 x 6 크기를 가짐

일반적으로 CNN에서는 레이어가 깊어질 수록 너비와 높이는 감소하고 깊이(채널)은 증가한다.
이때 각 채널은 서로 다른 특징(feature)을 적절히 추출하도록 학습되므로, 다양한 특징들을 조합하여 적절히 분류를 수행하게 된다.
예를 들어 가장 기본적인 형태의 LeNet을 확인해보면, 레이어가 깊어질수록 너비와 높이는 감소하고 채널은 증가하는 것을 확인할 수 있다.
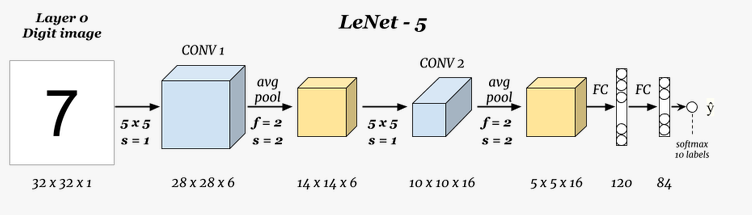
조금 더 자세한 예시는 아래 링크에서 확인해보자
CNN 수행과정
CNN 의 전체 네트워크 구조
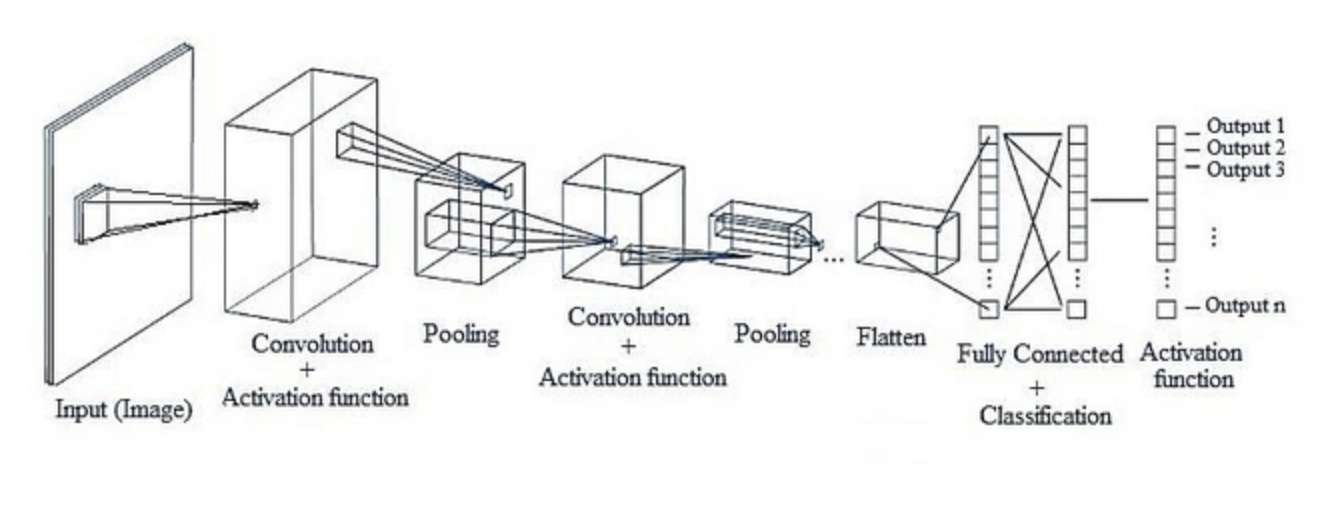
CNN 의 구조는 기존의 Fully-Connected Layer 와는 다르게 구성되어 있다.
Fully-Connected Layer(또는 Dense Layer라고도 함) 에서는 이전 계층의 모든 뉴런과 결합되어 있는 Affine Layer 으로 구현했지만, CNN은 Convolutional Layer 과 Pooling Layer 들을 활성화 함수 앞뒤에 배치하여 만들어진다.
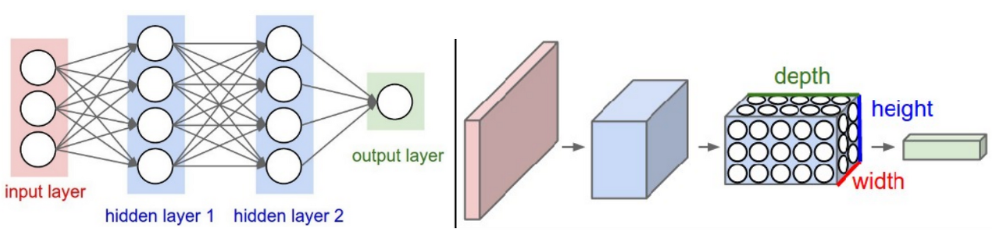
CNN의 각 레이어는 너비(width), 높이(height), 깊이(dept)로 구성됨. 일반적인 MLP와 비교했을 때 깊이(depth)가 추가되었다.
CNN 을 구성하는 layers
- 입력 레이어: 입력 이미지가 들어오는 레이어
- 컨볼루션 레이어: 입력 이미지의 일부 수용 영역(receptive field)에 대하여 컨볼루션 연산을 수행
- ReLU 레이어: 일반적으로 사용되는 activation function
- Pool 레이어: 너비(width) 와 높이(height)에 대해 downsampling 수행
- FC 레이어: 네트워크의 마지막 부분에서 실질적으로 클래스 분류 수행
CNN의 일반적인 구조
가장 일반적인 CNN의 패턴은 다음과 같다. 결과적으로 마지막 FC 레이어를 거쳐 클래스 분류 겨로가가 나오게 된다. LeNet 이후에도 굉장히 다양한 CNN이 등장했으나 대부분 아래와 같은 패턴을 따른다는 점이 특징이다.
INPUT -> [[CONV -> RELU] x N -> POOL] x M -> [FC -> RELU] x K -> FC
예시 1) INPUT -> FC
예시 2) INPUT -> CONV -> RELU -> FC
예시 3) INPUT -> [CONV -> RELU -> POOL]*2 -> FC -> RELU -> FC
각 계층을 자세히 살펴보면 아래와 같다.
1. 첫 번째 Convolutional Layer
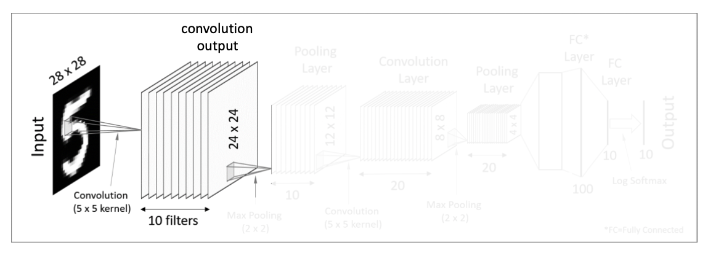
먼저 주어진 input 값은 28x28 크기의 이미지이다. 이 이미지를 대상으로 여러 개의 filter(kernel) 을 사용해 feature mapping(결과값)을 얻는다.
즉 한 개의 28x28 image input에 10개의 5x5 filters 를 사용해 10의 24x24 matrics(convolution 결과값)를 만들어내는 것이다. 이 결과값에 Activation function(ex. ReLU function) 을 적용한다.
여기까지 과정이 첫 번째 Convolutional Layer 에 해당되는 것이다.
이를 통해
A Convolutional Layer = convolution + activation
임을 알 수 있다.
Activation function 를 쓰는 이유
Activation function은 간단히 선형함수(linear function)인 convolution 에 비선형성(nonlinearity)를 추가하기 위해 사용하는 것이다.참고 자료
2. 첫 번째 Pooling Layer
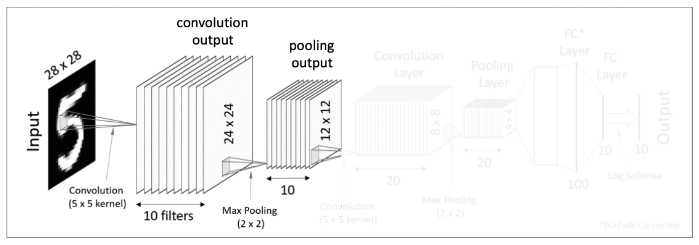
이전 단계에서 convolution 연산을 통해 많은 수의 결과값(이미지)들을 생성해는데, 한 개의 이미지에서 10개의 이미지 result maps 가 도출되면 값이 너무 많아져 문제가 된다. 이러한 문제를 해결하기 위해 고안된 것이 Pooling 이다.
Pooling 은 각 feature map 의 dimentionality를 축소해 주는 것을 목적으로 둔다. 즉 correlation 이 낮은 부분을 제거하여 각 결과값의 size (dimension) 을 줄이는 과정이다.
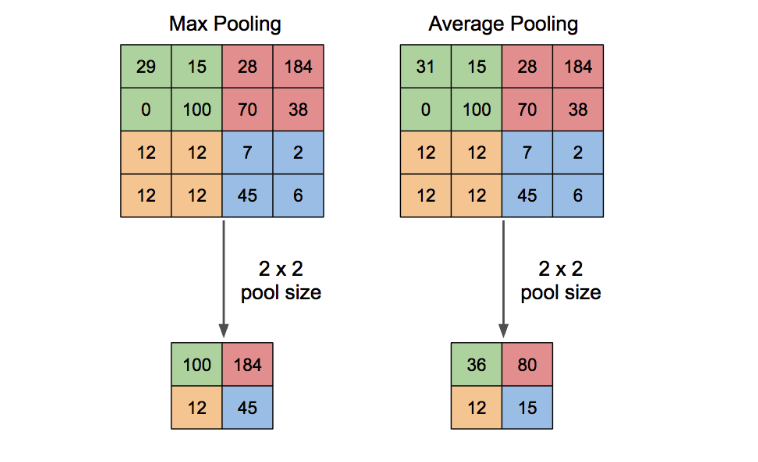
Pooling의 대표적 두 가지 방법인 Max pooling 과 Average pooling 이 있다.
위와 같이 Pool 의 크기가 2x2인 경우 2x2 크기의 matrix에서 max 나 average 를 가져와 결과값의 크기를 반으로 줄여주게된다.
즉 전체 네트워크에서는 Pooling Layer를 통해 10개의 24x24 matrics 에서 12x12 matrics 로 줄여진 것이다.
Pooling 을 쓰면
- input size 를 Down Sampling -> 텐서의 크기를 줄임
- overfitting 조절 -> 쓸데 없는 parameter 수를 줄임, 이를 통해 과적합을 방지
- 특징을 보다 잘 추출 -> 이미지 내의 특정한 모양을 더 잘 인식 (ex 새의 부리)
- 지역적 이동에 노이즈를 줘 일반화 성능을 높임 (maxpooling의 경우 주어진 픽셀 중 큰 것만 뽑기 때문에 모양이 조금 달라지는 특성을 가짐)
3. 두 번째 Convolutional Layer
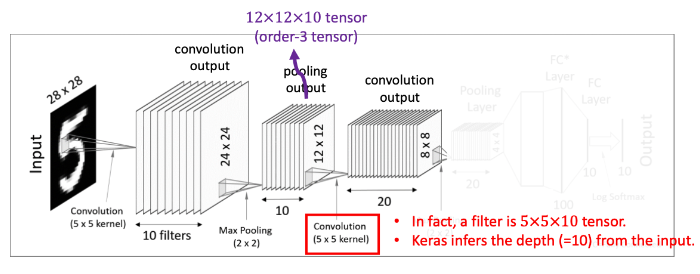
이번 Convolutional layer 에서는 tensor convolution을 적용한다. 이전의 pooling layer에서 얻어낸 12x12x10 tensor (order-3 tensor)를 대상으로 5x5x10 크기의 tensor filter 20개를 사용해 준다.
따라서 output으로 8x8 size를 가진 result map 20개를 얻어낼 수 있다.
4. 두 번째 Pooling Layer
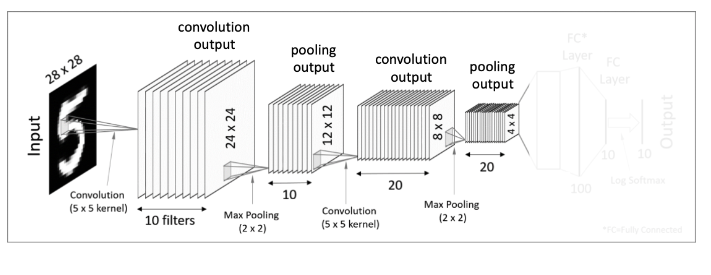
두 번째 Pooling layer는 이전과 똑같은 방식으로 Pooling 과정을 처리해주면 더 크기가 작아진 20개의 4x4 결과값을 얻는다.
5. Flatten (Vectorization)
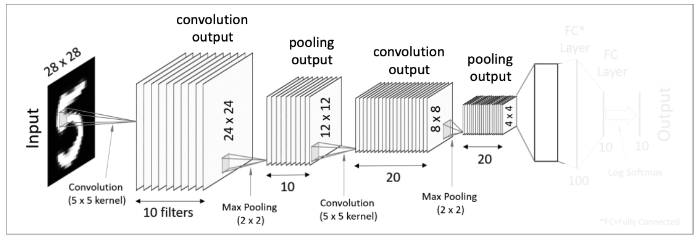
두 번째 Pooling Layer 에서 나온 output 인 4x4x20 tensor를 일자 형태의 데이터로 쭉 펼쳐주는 것을 Flatten 또는 Vectorization 이라고 한다.
쉽게 각 세로줄을 일렬로 쭉 세워두는 것이다. 그러면 이것은 320-dimension 을 가진 vector형태가 된다.
1차원 데이터로 변형해도 상관이 없을까?
이 전 두 번째 Pooling layer 에서 얻어낸 4x4 크기의 이미지들은 이미지 자체라기 보다는 입력된 이미지에서 얻어온 특이점 데이터가 된다.
즉 Pooling output은 이미 1차원의 벡터 데이터로 변형시켜주어도 무관한 상태인 셈이다.
6. Fully-Connected Layers (Dense Layers)
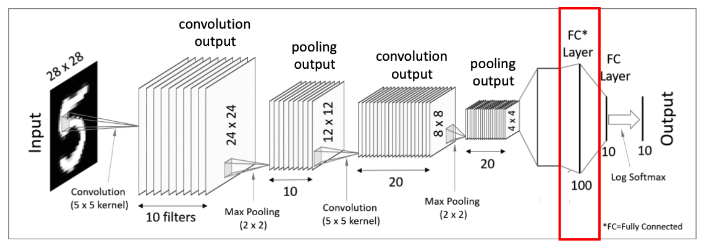
마지막으로 하나 혹은 하나 이상의 Fully-Connected Layer를 적용시키고 마지막에 Softmax activation function을 적용해주면 드디어 최종 결과물을 출력하게 된다.
Parameter 와 Hyper-parameter
Parameter, Hyper-parameter 내용 참조
parameter(모델 매개변수)는 모델 내부에 있으며 데이터로부터 값이 추정될 수 있는 configuration variable(설정 변수) 이다. Hyper-parameter 는 모델 외부에 있으며 데이터로부터 값이 추정될 수 없는 설정변수이다.
딥러닝의 기본은 파라미터들을 최적의 값으로 빠르고 정확하게 수렴하는 것을 목적으로 한다. 따라서 어떻게 모델의 파라미터들을 최적화 시키냐 하는 것은 모델 트레이닝의 중요한 포인트이다.
모델을 학습시킬 때 좋은 하이퍼파라미터를 찾는 것 또한 중요하다. 이것을 Tune Hyper parameters 라고 표현한다.
1. 학습 가능한 매개변수의 수
CNN 모델의 학습 가능한 매개변수(trainable parameters) 는 몇 개인지 확인해보자.
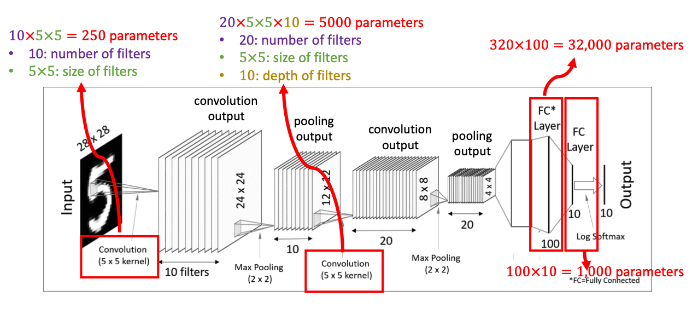
- 첫 convolution 과정에서 5x5 크기의 filter 10개를 사용하였으므로 250개의 매개변수가 존재한다.
- Pooling layer 에서는 단순히 크기를 줄이는 개념이므로 매개변수가 없다
- 두 번째 convolution 과정에서 5x5x10 크기의 tensor 20개를 사용했으므로 5,000개의 매개변수가 추가
- 두 개의 Fully-connected layer 들에서 각각 매개변수 32,000ro, 1000개가 추가
결과적으로, 생략한 intercepts 값까지 고려해보면 총 38,250 이상의 학습 가능한 매개변수를 갖게 된다.
2. Hyper-parameters
마지막으로 CNN 모델에서 튜닝 가능한 하이퍼파라미터는 어떤 것들이 있는지 간단히 살펴보자.
- Convolutional layers : 필터의 개수, 필터의 크기, stride 값, zero-padding 의 유무
- Pooling layers : Pooling 방식 선택 (MaxPool or AvgPool), Pool의 크기, Pool stride 값(overlapping)
- Fully-connected layers : 넓이 (width)
- Activation function : ReLU(가장 주로 사용되는 함수), SoftMax(multi class classification), Sigmoid(binary classification)
- Loss function : Cross-entropy for classification, L1 or L2 for regression
- Optimization 알고리즘과 이것에 대한 hyperparmeter(보통 learning rate): SGD(Stochastic gradient descent), SGD with momentum, AdaGrad, RMSprop
- Random initialization : Gaussian or uniform, Scaling
다양한 CNN 아키텍처
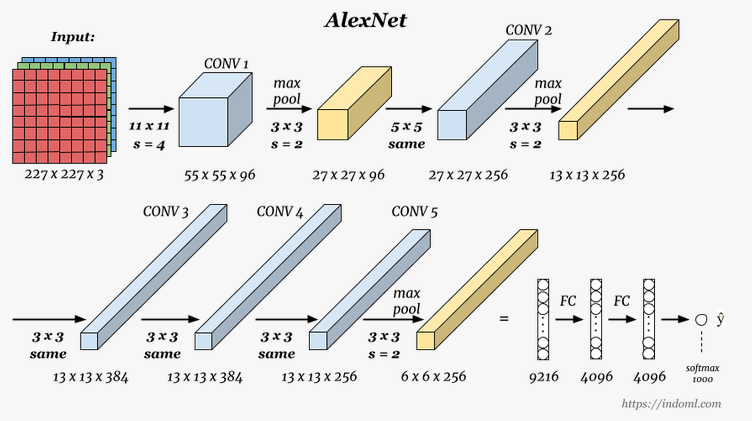
1) AlexNet
이미지 분류 (Image Classification)에서 CNN이 큰 주목을 받게 해 준 네트워크다. ILSVRC 2012에 출전하여 압도적인 성능 차이를 보였다. CONV 레이어 이후에 바로 풀링 레이어를 넣지 않고, CONV를 중첩해서 사용했다는 점이 특징이다.
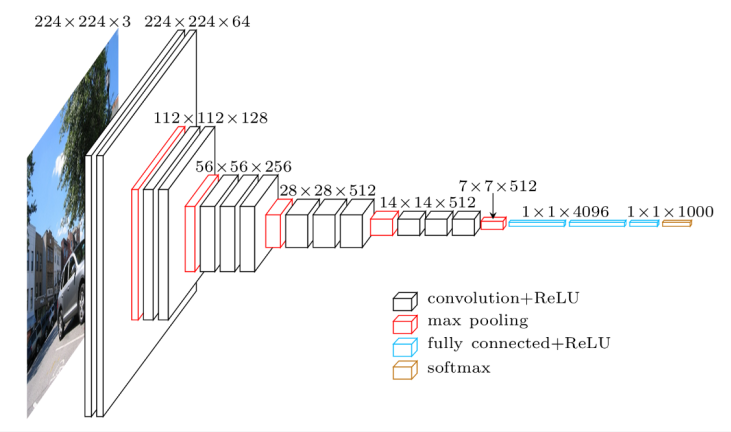
2) VGGNet
IL SVRC 2014에서 2등을 한 네트워크다. VGG에서는 레이어를 깊게 쌓았을 때 더 좋은 성능이 나올 수 있다는 것을 보여주었다. 16개의 레이어로 구성되는 VGG-16이 대표적이다.
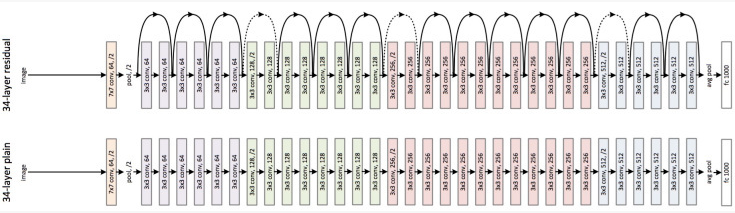
3) ResNet
ILSVRC 2015년에서 1등을 한 네트워크인 ResNet는 skip connection과 배치 정규화(batch normalization)를 사용했다는 점이 특징이다. 지금은 매우 많은 네트워크에서 skip connection과 배치 정규화를 사용하고 있으며, 2020년 까지도 ResNet은 많은 논문에서 baseline 으로 성능 비교 대상이다.