좋은 기회로 참여하게 된 원티드 pre onboarding에서 어느새 3주차를 접어 들었다
1주차에 다양한 NLP subtasks 의 SOTA model들을 리서치해보는 과제를 4일에 걸쳐 진행했는데, 모두 다른 모델이었지만 Transformer model을 포함한 경우가 많았다. (아마 BERT에서 develop된 모델들이 대다수 SOTA 를 차지해서 그런듯 하다.)
1주차에는 처음 접하는 NLP 가 어색하기도 하고 과제 마감에 급해
속으로 그래서 Transformer 가 뭔데 .. ! 생각만 하고 지나갔다

결국 오늘에서야 Transformer model 논문인
Attention Is All You Need 를 읽고 요약해보려 한다
Index
1. Introduction
2. Background
3. Model Architecture
+) 요약 필기
위와 같은 순서로 작성할 것이며, 아래 원문과 레퍼런스를 참고해
작성했다
Transformer
1. Introduction
Introduction에 앞서 Abstract를 먼저 보자

기존 transduction model은 RNN or CNN 기반이 대부분이다
이에 이 논문은 새로운 network architecture인 Transformer를 제안한다
해당 모델은 두가지 기계번역 tasks에서 좋은 품질을 가지며 더욱 병렬화된 계산과 학습시간을 감소시키는데 성공한다
그 결과 WMT 2014~ 에서 28.4 BLEU를 기록했고
이는 앙상블 모델을 포함한 최고 결과와 비교했을 때 2 BLEU가 더 높다
또한 다른 task에서도 state-of-the-art BLEU scroe 인 41.8을 기록했다
기록 뿐 아니라 training cost 또하 적은 편이며 일반적으로 다른 tasks에서도 좋은 성능을 보인다.
Introduction

기존에 많이 사용되던 RNN 모델은 순차적인 특성 때문에 병렬계산이 불가하고
시퀀스가 길어질 수록 배치처리가 어려워지는 문제가 있다
factorization triks 로 어느정도 performance를 개선했지만,
순차개선 문제는 해결하지 못했다.
Attention mechanism은 시퀀스 모델링을 통해 input과 output 간의 거리와 상관없이 dependecies를 모델링하게 한다.
하지만 이 매커니즘 역시 대부분 RNN과 함께 사용되었다.
Transformer는 RNN 모델을 배제하고 Attention mechanism 만을 전적으로 사용한다
이를 통해 병렬화를 더욱 많이 가능하게 하고 번역 부분에서 state of the art 를 달성했다
2. Model Architecture
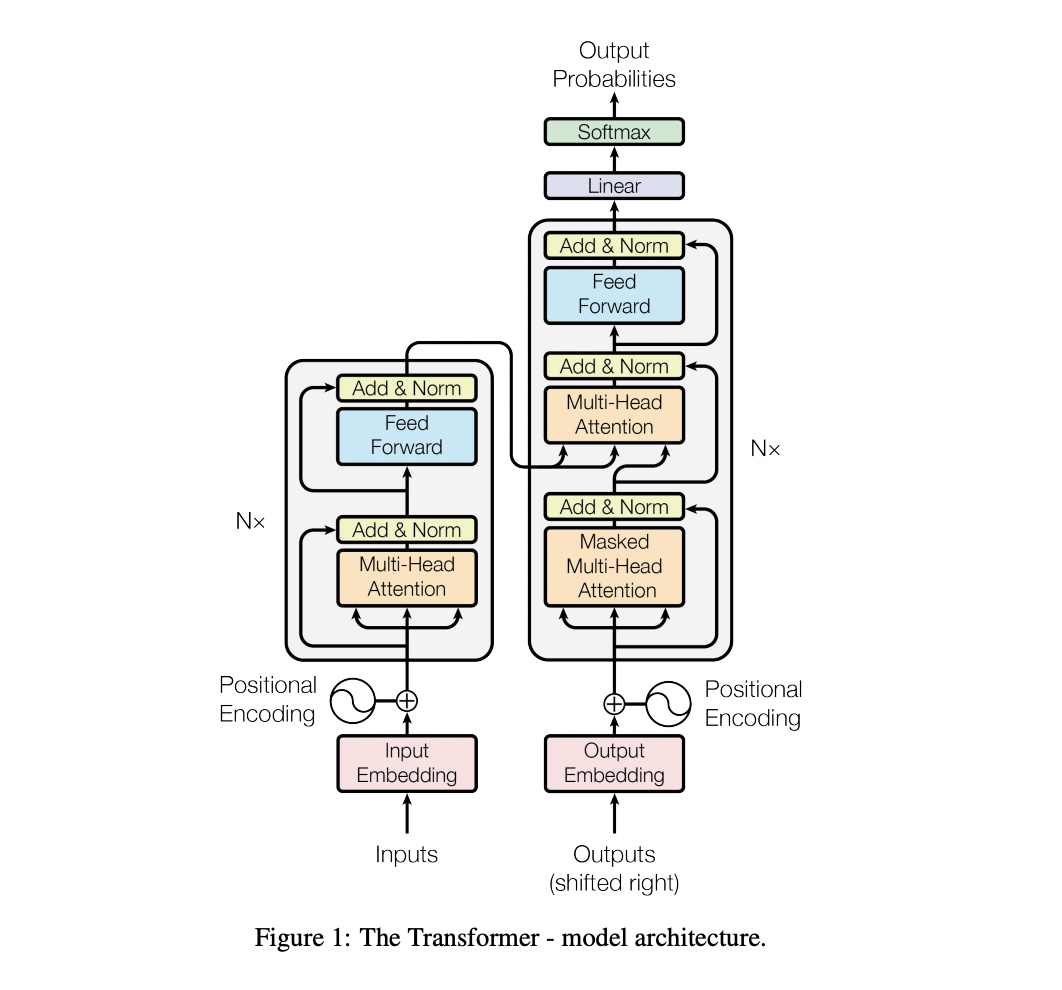
논문에서 가져온 위의 사진은 Transformer 의 architecture를 시각화 한 것이다
encoder-decoder 구조로 encoder, decoder 가 각각 N개 stack 된 구조이다
decoder 에서 출력되는 최종 output은 Linear & Softmax layer 를 거쳐 확률로 나타내진 벡터를 통해 문장을 만들어낸다.
그럼 각 구성마다 가지는 기능을 자세히 알아보자
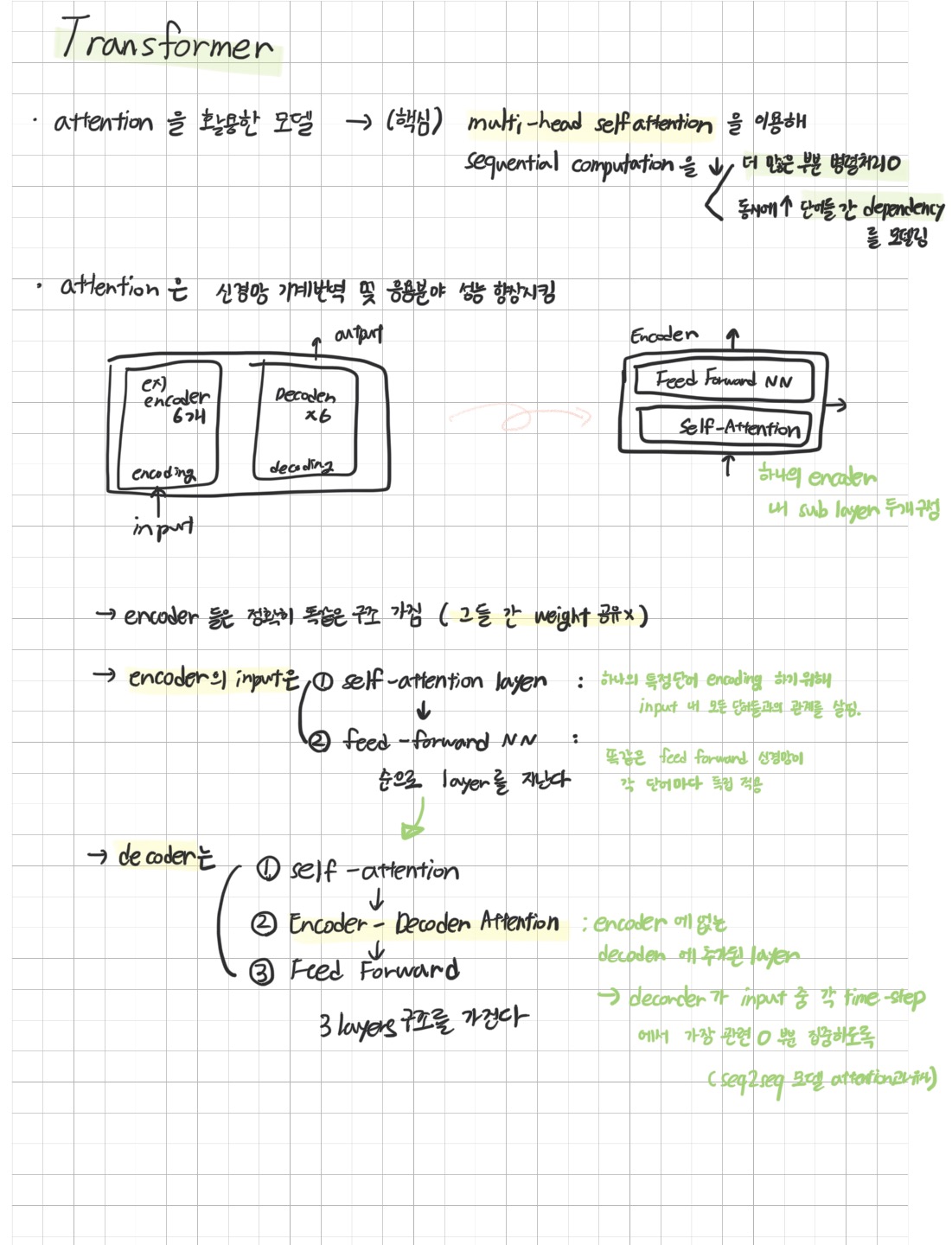
Encoder
encoder 는 multi-head attention layer, Feed-Forward layer 과 그 둘을 연결하고 Normalization 하는 residuals 로 구성되어 있다
Multi-Head Attention
Mult-Head Attention은 간단히 self attention 에 Multi-Head를 적용한 것이다
여기서 self attention을 사용하는 이유는 같은 단어의 다른 뜻을 구분하기 위해
encoding의 target이 되는 단어 외 다른 단어들에서 힌트를 얻어
target 단어를 더 잘 encoding 하기 위함이다.
self attention (Scaled Dot-Product Attention)은
아래 사진과 같이 작동한다
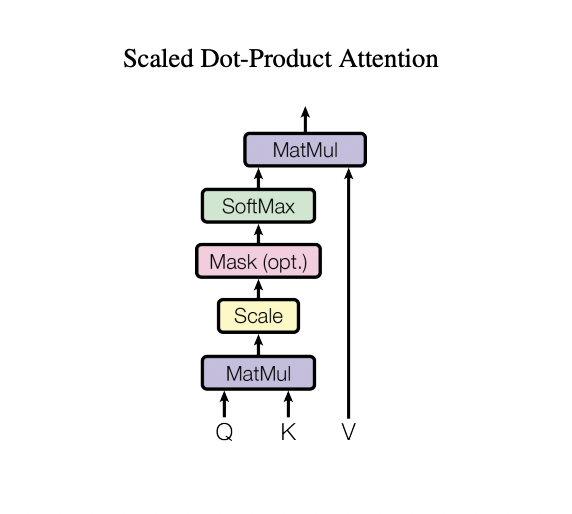
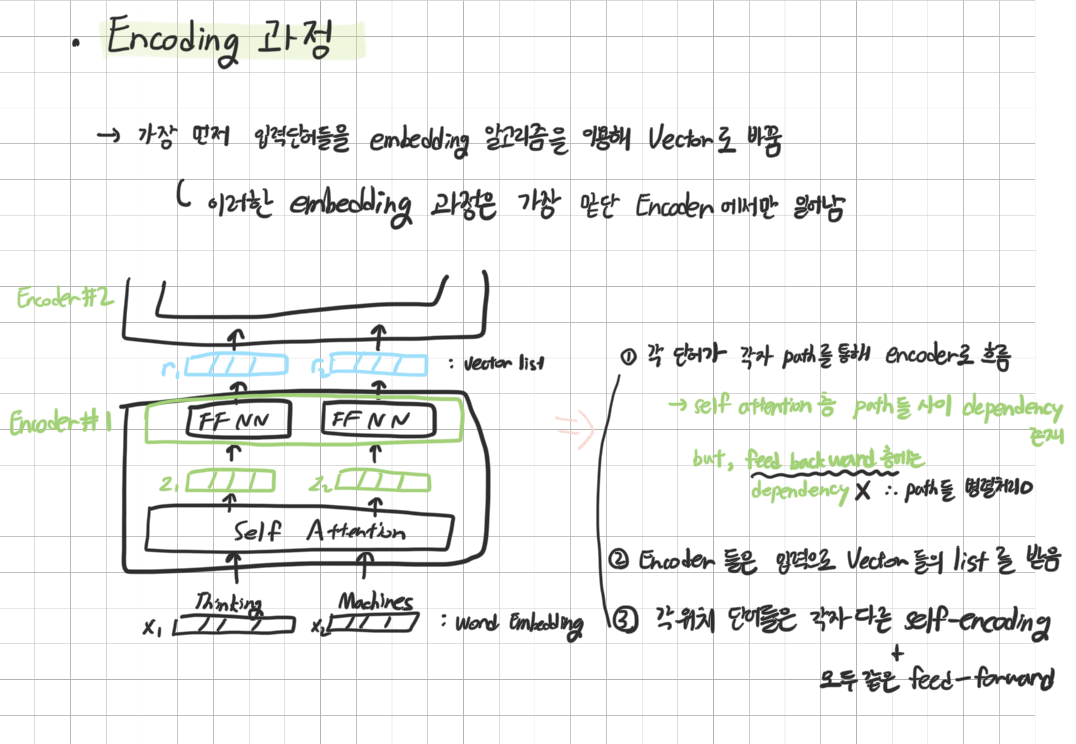
input embedding 과 positional encoding을 거친 벡터가 layer로 들어오면 Query, Key, Value 세가지 벡터로 만든다.
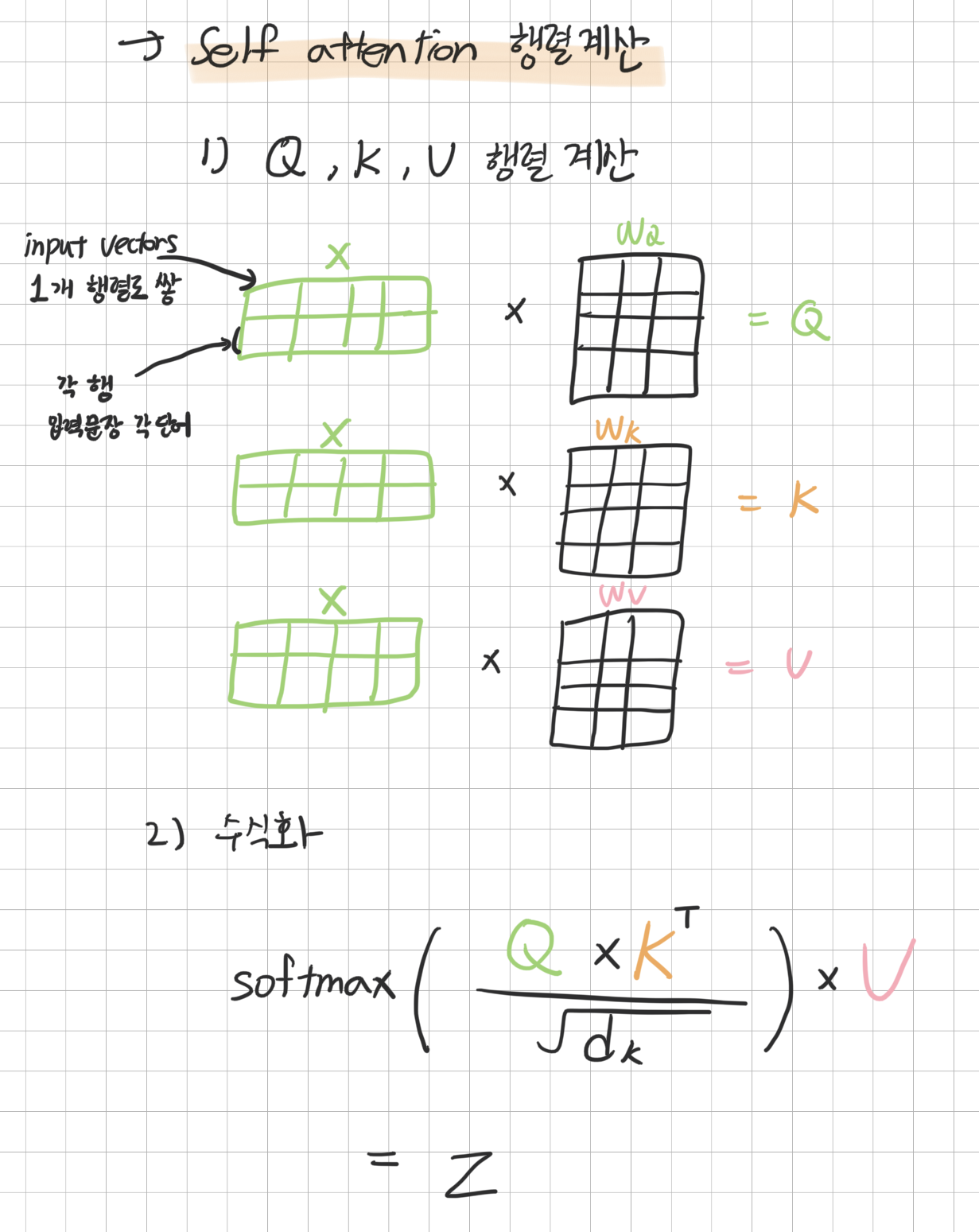
input vector 를 X로 가정하면 Query, Key, Value 를 생성하는 각각의 weights W를 곱해 Query, Key, Value vector 를 생성시킨다
생성된 3 벡터를 위의 그림에서는 Q, K, V 로 나타내었다
Q, K, V 를 그림과 같은 과정으로 계산을 마치면 feed-forward layer 로 가는 output 벡터가 산출된다
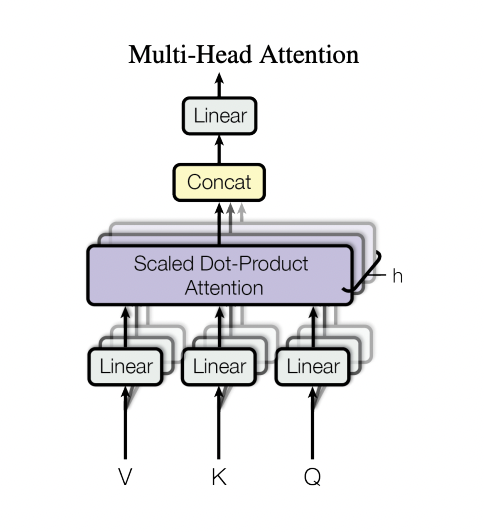
self-attention은 위의 과정만으로 다음 layer 로 전달될 수 있지만
transformer 모델의 특징인 Multi-Head 의 경우
Scaled Dot-Product 를 통해 산출되는 벡터가 여러개이므로
바로 전달될 수 없다 (vector size가 맞지 않아서)
따라서 모든 산출 벡터를 concat 한 후 1개가 된 벡터를
size가 맞는 weight matrix로 내적해 feed-forward에 맞는 size의 벡터로 변환시켜 준다 (1개의 벡터)
아래는 이 내용을 수식으로 표현한 것이다

이러한 Multi-Head Attention은 self attention 보다
1) 모델이 다른 위치에 집중하는 능력을 확장시키고
2) attention layer 가 여러개의 representation 공간을 갖게 하는 이점이 있다
Positional Encoding
위의 기능 만으로는 단어들의 순서까지 고려하기는 어렵다
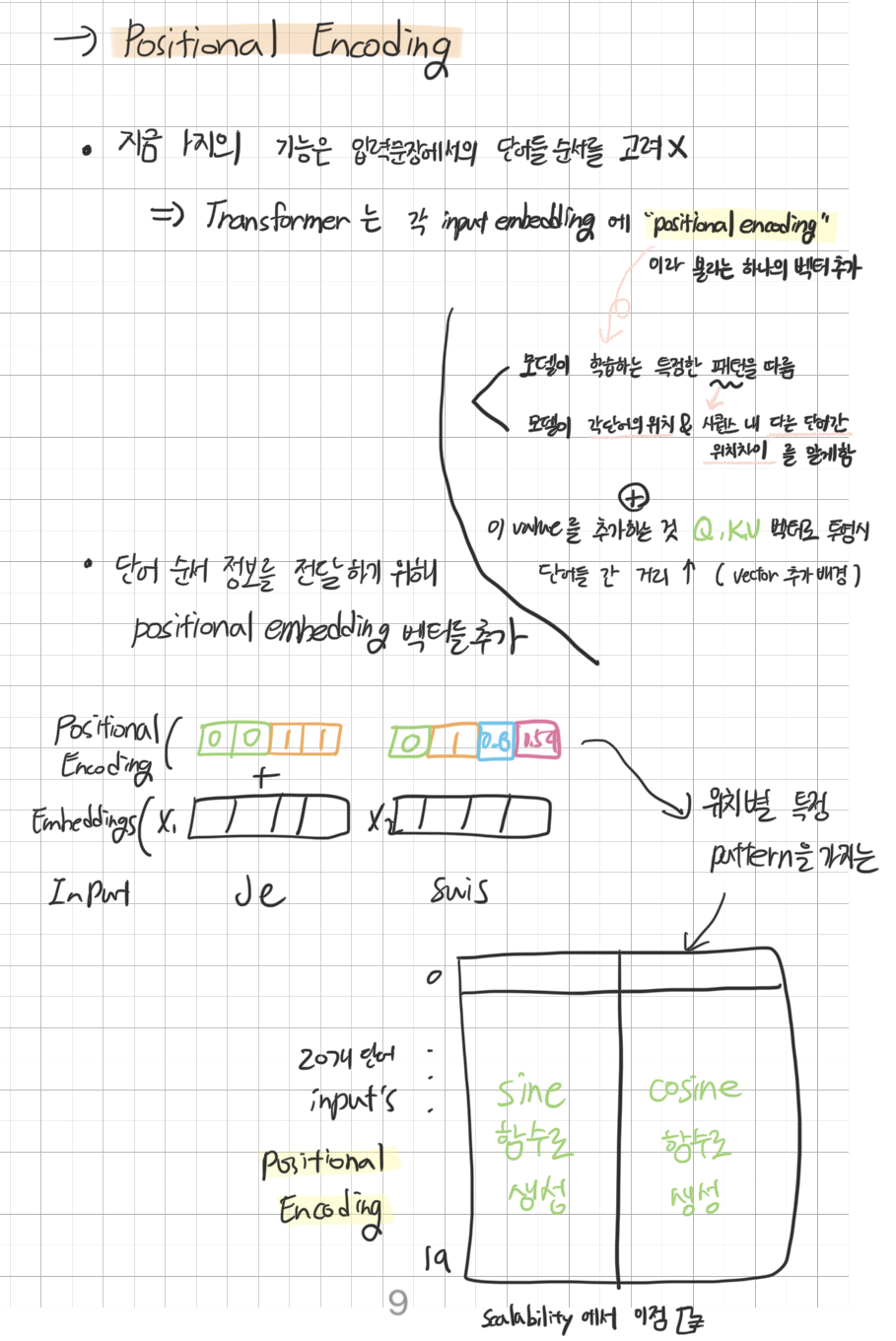
따라서 Transformer는 각 input embedding에 "positional embedding"이라 불리는 벡터를 하나 추가한다
positional embedding은
모델이 학습하는 특정한 패턴을 따르며
모델이 각 단어의 위치 & 시퀀스 내 다른 단어 간 위치의 차이를 알도록 돕는다
또한 이 벡터를 추가할 시 앞에서 언급한 Q, K, V 벡터로 투영할 때
단어들 간 거리를 더 늘릴 수 있다
그냥 한 줄로 요약하면 "단어 순서 정보를 전달하려고.." 이 벡터를 추가하게 된 것이다
positional embedding 벡터를 시각화 하면 중간이 세로로 나누어저 있는데
왼쪽은 sine 함수로 생성, 오른쪽은 cosine 함수로 생성하기 때문이다
(시각화 자료는 위의 reference1에서 볼 수 있다)
Feed-Forward

Multi-Head attention과 Add&Normalize 를 거치면
Feed Forward에 전달되는데
각 단어마다 개별적으로 작동하며
두개의 linear transformations 으로 구성되었고 중간에 ReLU activation이 있는 구조이다
Decoder
decoder 는 가장 윗단의 encoder output 을 입력받고
Attention layer 에서 K, V 로 변환시킨다
생성한 두 벡터는 encoder-decoder attention layer 에서 decoderrk input sequence의 적절한 위치에 집중하도록 돕는 역할을 한다
decoding 의 각 step은 output sequence의 1개 element씩 출력한다
출력된 단어는 다음 step 가장 밑단 decoder로 전달되게 된다
encoder 와 decoder 에서 하는 작업이 거의 유사한데
두가지 차이점이 존재한다
- output 내 현재위치의 이전위치에 대해서만 attention 한다
(softmax 를 취하기 전 masking 작업 통해)- encoder 와는 다르게 K, Q 행렬을 encoder output에서 가져온다
(단, Q 는 decoder 하단 layer 에서 발생)
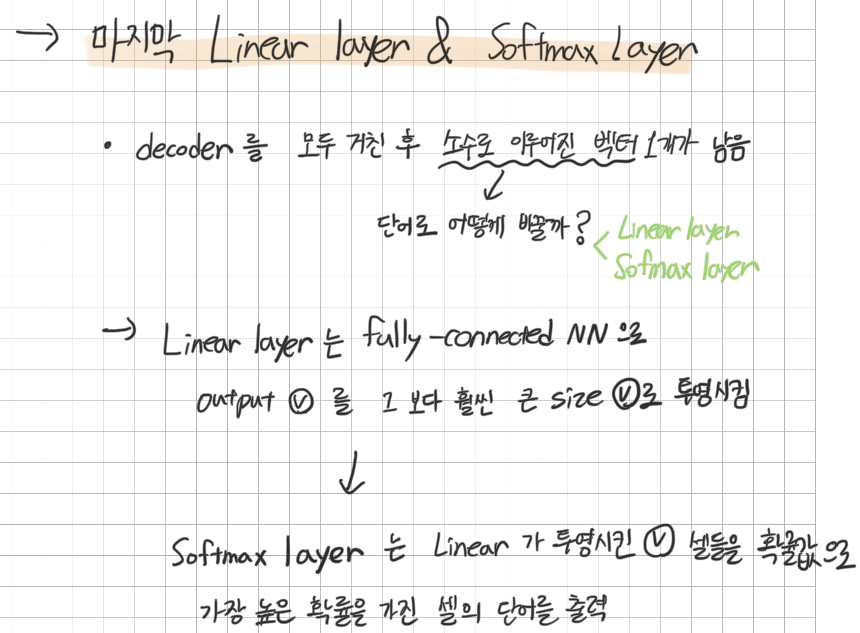
Linear layer & Softmax layer
decoder 를 모두 거친 후에는 소수로 이루어진 벡터 1개가 남게 된다
이것을 단어로 바꾸는게 liner & softmax layer 이다.
Linear layer 는 fully-connected NN 으로 output 벡터를
그 보다 훨씬 큰 size 벡터로 투영시킨다
size가 늘어난 벡터를 softmax를 통해 확률값으로 변환시키고
가장 높은 확률을 가진 셀의 해당하는 단어가 하나의 위치마다 하나씩 출력된다
지금까지 아래 사진의 transformer architecture를 글로 요약해 보았다
잘게 씹어서 이해하고 보니 처음에는 생소했던 아래 그림이 바로 이해가 되는 magic,,

논문의 뒷부분인 train 과 result도 요약하고 싶지만 시간관계상 추후에 추가하기로 하고, 논문을 이해하기 위해 나름대로 끄적인 필기를 올리고 마무리하려 한다.
+) 요약 필기
내놓기 부끄러운 글씨체이지만
아이패드만 열면 유튜브 보고싶기 때문에
블로그에 옮겨두는게 더 자주 볼것 같아 올리게 된다 🤓