1️⃣ 코사인 유사도란?
코사인 유사도(Cosine Similarity)는 두 개의 벡터 간 각도를 기반으로 유사도를 측정하는 방법이다.
- 벡터의 크기(길이)는 고려하지 않고, 방향만 비교한다
- 두 벡터의 각도가 작을수록(= 같은 방향일수록) 유사도가 높음
- 값의 범위: -1(완전 반대) ≤ 코사인 유사도 ≤ 1(완전 동일)
1에 가까울수록 두 벡터(문장)가 유사함
0에 가까우면 관련성이 낮음
-1에 가까우면 완전히 반대 의미
- 텍스트 유사도 분석에서는 일반적으로 0~1 범위로 변환
2️⃣ 코사인 유사도 공식
코사인 유사도는 두 벡터 𝐴와 𝐵사이의 각도 𝜃를 이용해 정의된다.
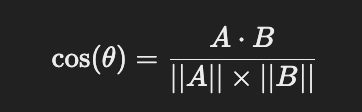
3️⃣ 코사인 유사도 계산 예제
📌 1) 두 개의 벡터 정의
예를 들어, 다음 두 개의 문장이 있다고 하자.
문장 1: "나는 축구를 좋아해."
문장 2: "나는 농구를 좋아해."SBERT(BERT 기반 임베딩 모델)로 변환된 벡터가 다음과 같다고 가정하자.
(※ 실제로는 수천 개의 차원을 가지지만, 이해를 위해 3차원 예제 사용)
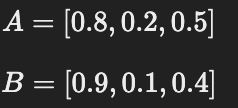
📌 2) 벡터 내적 계산 (𝐴⋅𝐵)
A⋅B=(0.8×0.9)+(0.2×0.1)+(0.5×0.4)
=0.72+0.02+0.20
=0.94 📌 3) 벡터 크기 계산
벡터 크기는 유클리드 거리(Euclidean Norm, L2 Norm) 를 사용하여 계산한다.
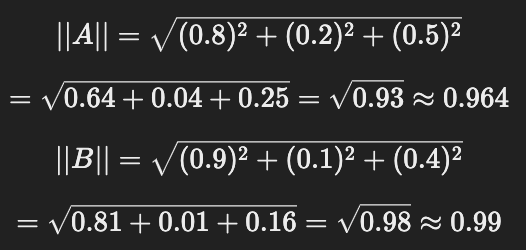
📌 4) 코사인 유사도 계산
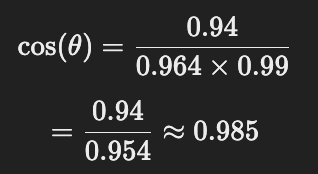
👉 최종 코사인 유사도 = 0.985
즉, "나는 축구를 좋아해." 와 "나는 농구를 좋아해." 는 98.5% 유사한 문장임! 🎯
4️⃣ 코사인 유사도의 특징
✅ 1) 방향만 고려하고 크기는 무시
두 문장이 같은 의미를 가지면 벡터의 크기와 상관없이 높은 유사도를 가짐.
문장이 짧거나 길어도 의미만 같다면 유사하게 측정됨.✅ 2) 텍스트 비교에 적합
문서 유사도, 검색 엔진, 챗봇 시스템, 질문-답변 시스템 등에 사용됨.✅ 3) 빠른 계산 속도
곱셈과 루트 연산만 사용하므로 빠르게 처리 가능.
```
import numpy as np
def cosine_similarity(vec1, vec2):
""" 두 벡터의 코사인 유사도를 계산하는 함수 """
dot_product = np.dot(vec1, vec2) # 내적 계산
norm_vec1 = np.linalg.norm(vec1) # 벡터 A 크기 계산
norm_vec2 = np.linalg.norm(vec2) # 벡터 B 크기 계산
return dot_product / (norm_vec1 * norm_vec2) # 공식 적용
# 예제 벡터 (3차원)
vec_a = np.array([0.8, 0.2, 0.5])
vec_b = np.array([0.9, 0.1, 0.4])
# 코사인 유사도 계산
similarity = cosine_similarity(vec_a, vec_b)
print(f"코사인 유사도: {similarity:.4f}")
```
```
코사인 유사도: 0.9852
```즉, 두 문장은 약 98.5% 유사함!
6️⃣ BERT 기반 코사인 유사도 적용 (실제 사용 코드)
실제 SBERT 모델을 사용해 두 문장의 유사도를 계산하는 방법! 🚀
from sentence_transformers import SentenceTransformer, util
# SBERT 모델 로드
bert_model = SentenceTransformer("sentence-transformers/all-MiniLM-L6-v2")
# 비교할 문장
sentence1 = "나는 축구를 좋아해."
sentence2 = "나는 농구를 좋아해."
# 문장을 벡터(임베딩)로 변환
embedding1 = bert_model.encode(sentence1, convert_to_tensor=True)
embedding2 = bert_model.encode(sentence2, convert_to_tensor=True)
# 코사인 유사도 계산
similarity_score = util.pytorch_cos_sim(embedding1, embedding2).item()
print(f"코사인 유사도: {similarity_score:.4f}")
코사인 유사도: 0.8753
🎯 BERT 모델을 활용하면 문장 간의 의미적 유사도를 더욱 정교하게 측정할 수 있다!
📌 결론
1️⃣ 코사인 유사도는 두 벡터 간 방향 차이를 기반으로 유사도를 계산하는 방법!
2️⃣ 텍스트 비교에 최적화되어 문장 간 의미적 유사도를 효과적으로 측정 가능!
3️⃣ BERT 모델과 결합하면 더 정교한 문장 의미 비교가 가능! 🚀🔹 예제:

👉 즉, 코사인 유사도를 활용하면 문장의 의미적 유사성을 정량적으로 평가 가능! 🎯
