데이터 수(n)에 따른 시간 복잡도 함수(T(n))을 정확하게 구하는 것은 대부분 쉽지 않다.

시간복잡도 함수 T(n)은 근사치(approximation) 식을 구성해도 문제가 되지 않는다

시간복잡도 함수가 $T(n) = n^2 + 2n + 1$와 같다면 $T(n) = n^2 + 2n$로 간략화해도 된다.

그리고 더 나아가 $T(n) = n^2$와 같이 간략화해도 문제가 없다

이는 수학적으로 봤을 때 $2n$은 뺏을 때 값에 많은 영향을 줄 것 같지만 그렇지 않다. 아래 표를 보면 알 수 있다.

$n$	$n^2$	$2n$	$T(n)$	$n^2$의 비율
10	100	20	120	83.33%
100	10,000	200	10,200	98.04%
1,000	1,000,000	2,000	1,002,000	99.80%
10,000	100,000,000	20,000	100,020,000	99.98%
100,000	10,000,000,000	200,000	10,000,200,000	99.99%

위 표는 임의의 값 $n$이 있을 때 $n^2$이 차지하는 비율을 나타낸다.
비율을 살펴보면 $n$의 값이 커질수록 $n^2$이 차지하는 비율은 확실히 커지게 된다.

따라서 $T(n) = n^2 + 2n + 1$를 $T(n) = n^2$로 표현할 수 있다.
그리고 위 함수를 빅-오 표기법으로 표현하면 $O(n^2)$과 같이 표현할 수 있다.

그리고 이를 일반화하면 다음과 같다.
$T(n) = a_mn^m + a_{m-1}n^{m-1} + \cdots + a_ln^l + a_0 \Rightarrow O(n^m)$

즉, 다항식으로 표현된 시간 복잡도 함수 $T(n)$에서 큰 의미를 갖는 것은 '최고차항의 차수($n^m$)'이다

이는 최고차항이 $9999n^2$일때도 똑같이 $n^2$이 된다.

그럼 계수가 9999인 것은 꽤나 큰 의미를 가질텐데 왜 그럴까??
이는 다음과 같다
데이터의 수(n)가 5개일 경우 연산 횟수의 증가가 각각 $5^2 = 25$, $9999 \times 5^2 = 249975$로 둘의 차이가 크다.

하지만 빅-오의 관점에서는 다음과 같이 본다
데이터의 수가 2, 3, 4개로 늘어날 때 연산횟수는 4, 8, 16으로 두배씩 증가
데이터의 수가 2, 3, 4개로 늘어날 때 연산횟수는 99, 198, 396으로 두 배씩 증가

결론적으로 2배씩 증가하는 것은 같다.
이는 $O(log { n})$으로 데이터 증가에 따른 연산횟수의 증가 형태를 좌표평면상에 그리면 증가하는 추세가 둔화되는 형태를 띈다. (로그 그래프와 유사한 형태를 그린다)

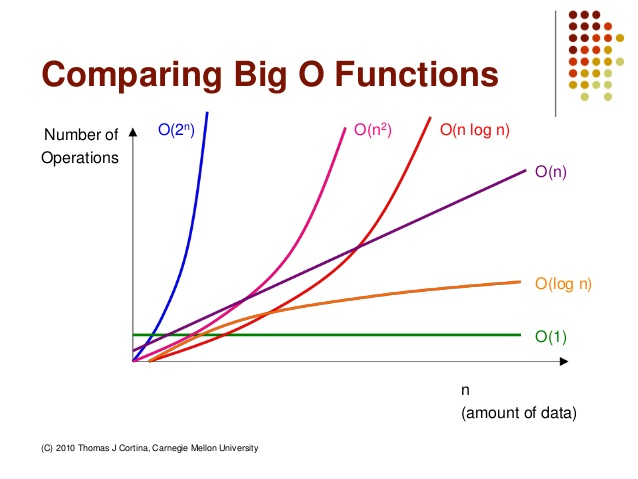
대표적인 빅-오

$O(1)$

• 상수형 빅-오라고 한다.
• 데이터 수에 상관없이 연산횟수가 고정인 유형의 알고리즘을 의미
• 예를 들어 연산 횟수가 데이터 수에 상관없이 3회씩 진행되는 알고리즘이라도 $O(3)$가 아닌 $O(1)$이라고 한다.

$O(logn)$

• 로그형 빅-오라 한다.
• '데이터 수의 증가율'에 비해 '연산횟수의 증가율'이 훨씬 낮은 알고리즘을 의미
• 매우 바람직한 유형이다

$O(n)$

• 선형 빅-오라 한다.
• 데이터의 수와 연산횟수가 비례하는 알고리즘을 의미

$O(nlogn)$

• 선형로그형 빅-오라 한다.
• 데이터의 수가 두 배로 늘 때, 연산횟수는 두 배를 조금 넘게 증가하는 알고리즘을 의미
• $n$과 $logn$을 곱한 형태로 난해해 보이지만, 이에 해당하는 알고리즘이 적지 않음

$O(n^2)$

• 데이터 수의 제곱에 해당하는 연산횟수를 요구하는 알고리즘을 의미
• 데이터 양이 많은 경우 적용하기에 부적절
• 일반적으로 이중 중첩된 반복문 내에서 알고리즘 연산이 이루어지기 때문에 발생
• 중첩된 반복문의 사용은 알고리즘 디자인에서 그리 바람직하지 않다.

$O(n^3)$

• 데이터 수의 세 제곱에 해당하는 연산횟수를 요구하는 알고리즘을 의미
• 일반적으로 삼중 중첩된 반복문 내에서 알고리즘 연산이 이루어지기 때문에 발생
• 이 또한 제곱과 같이 적용하기에는 무리가 있는 알고리즘이다.

$O(2^n)$

• 지수형 빅-오
• 사용하기에 매우 무리가 있는, 사용하는 것 자체가 비현실적인 알고리즘
• 매우 무서운 연산횟수의 증가
• 만약 알고리즘이 이런 성능을 보이면, 개선의 과정을 거쳐 가장 현실적인 연산횟수를 보이는 알고리즘으로 수정되어야 한다.

빅-오의 성능 대소 정리

$O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n)$

빅-오 그래프

아래는 대표적인 빅-오의 '데이터 수의 증가에 따른 연산횟수 증가율'을 그래프로 정리한 것이다.