하노이 타워

하노이 타워는 재귀함수하면 항상 언급되는 대표적인 예제이다.
위 사진을 보면 어떤 것일지 알 것이다.

하노이 타워 문제 이해

하노이 타워는 하나의 막대에 쌓여있는 원반을 다른 막대에 옮기는 방법 문제이다.
하지만 그냥 옮기는 것이 아닌 제약조건을 만족시키면서 옮겨야한다.

하노이 타워 제약 조건

• 원반은 한 번에 하나씩 옮길 수 있다.
• 작은 원반 위에 큰 원반이 올라갈 수 없다.

그렇기 때문에 막대는 세 개가 존재하고 출발과 도착 막대를 제외한 중간에 도움을 주는 막대가 필요한 것이다.

간단한 예시로 원반이 세 개일때를 살펴보자

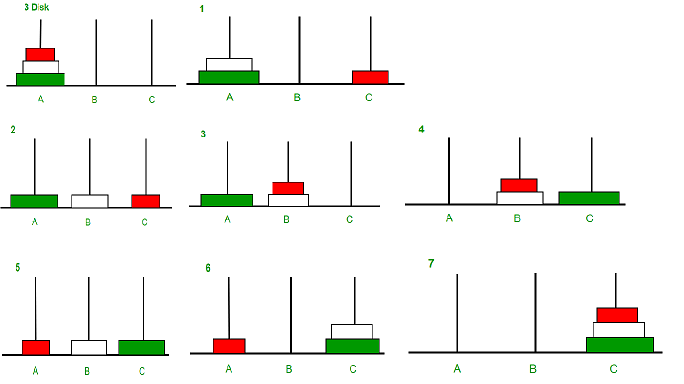
위 사진을 보면 원반이 세 개일때 어떻게 동작하는지 순서대로 보여준다.

위 과정을 보면 우선 가장 큰 원반을 제외한 두 개의 원반을 B막대에 옮겨놓은 후 가장 큰 원반을 C막대에 옮기고 다시 B막대의 원반들을 C막대에 옮긴다.

위 일련의 과정에서 보면 두 개의 원반을 A에서 B로 옮기는 것이 가장 우선적으로 해결해야하는 문제이다.

원반이 3개가 아니라 4개, 5개, 10개가 되어도 그것은 동일할 것이다.

그럼 n개의 원반을 A에서 C로 옮기는 과정을 정리해보자

하노이 타워 문제 해결

1. 작은 원반 n-1개를(가장 큰 원반을 제외한 나머지 원반) A에서 B로 이동
2. 큰 원반(맨 아래의 원반) 1개를 A에서 C로 이동
3. 작은 원반(1번에서 A에서 B로 이동한 원반) n-1개를 B에서 C로 이동

하노이 타워는 크게 세 동작으로 구분할 수 있다.
n개를 이동하는 문제는 n-1개를 이동하는 문제로, n-1개를 이동하는 문제는 n-2개를 이동하는 문제로 세분화된다.
결국, n개를 이동하는 문제는 1개를 이동하는 문제로 세분화되는 것이다.

그럼 함수로 작성해보자

void HanoiTowerMove(int num, char from, char by, char to) {}

우선 함수의 선언은 위와 같이 할 수 있다.
num개의 원반, from, by, to는 각각 A, B, C 막대로 보면 된다.

• num개의 원반을 by를 거쳐 from에서 to로 이동한다.

만약 이동해야할 원반의 개수가 1개일 경우는 아주 쉽게 그냥 옮기기만 하면 된다.

if (num == 1) {
	printf("원반 1을 %c에서 %c로 이동 \n", from, to);
}

그럼 1이 아닌 경우에는

} else {
	// 1단계
	HanoiTowerMove(num-1, from, to, by); 
    // 2단계
    printf("원반 %d을(를) %c에서 %c로 이동 \n", num, from, to); 
    // 3단계
    HanoiTowerMove(num-1, by, from, to); 
}

위 1단계~3단계는 앞에서 설명한 큰 세단계이다
파라미터를 잘 보면 from, by, to의 순서가 조금씩 다른 것을 볼 수 있다.

최종코드

#include <stdio.h>

void HanoiTowerMove(int num, char from, char by, char to) {
   if (num == 1) {
      printf("원반 1을 %c에서 %c로 이동 \n", from, to);
   } else {
      HanoiTowerMove(num-1, from, to, by);
      printf("원반 %d을(를) %c에서 %c로 이동 \n", num, from, to);
      HanoiTowerMove(num-1, by, from, to);
   }
}

int main() {
   // 원반 3개를 A막대에서 B막대로 옮기기
   HanoiTowerMove(3, 'A', 'B', 'C');

   return 0;
}