수식 트리

수식트리란 이진 트리를 이용해서 수식을 표현해 놓은 것을 가르켜 수식 트리라고 한다.

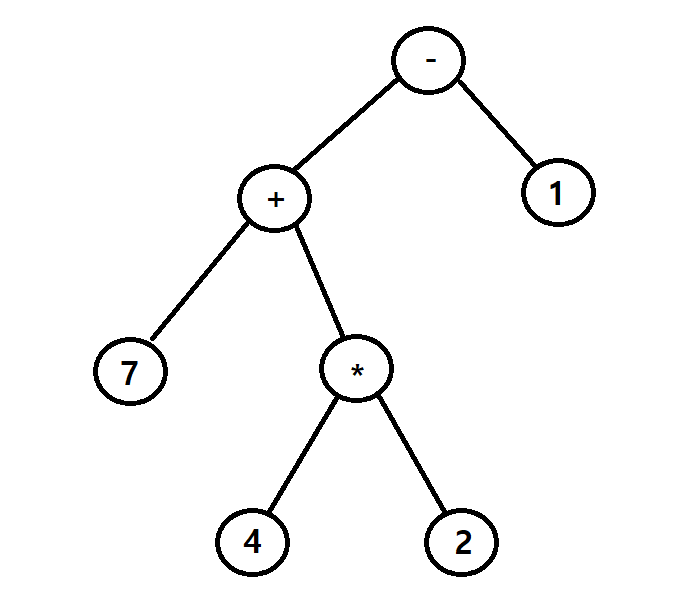
위 그림은 수식 7 + 4 * 2 - 1을 나타낸 수식 트리이다.

중위 표기법과 후위 표기법이 수식 표현의 한 가지 방법이듯 수식 트리도 수식을 표현하는 하나의 방법이다.

위 수식 트리는 가장 먼저 *이 진행되고 그 다음 +, - 순으로 연산이 진행된다

이진 트리와 스택을 구현한 코드를 그대로 사용한다.

후위 표기법 기반 수식 트리 구성

수식 1 2 + 7 *을 트리로 만들면 아래 그림과 같다

후위 표기법의 두 가지 특징

• 연산 순서대로 왼쪽에서 오른쪽으로 연산자가 나열
• 해당 연산자의 두 피연산자는 연산자 앞에 나열

수식 트리에서는 트리 아래쪽에 위치한 연산자들의 연산이 먼저 진행된다.
따라서 아래에서 위로 구성해나간다.
그림을 보면 먼저 등장하는 연산자와 피연산자를 이용해 트리 하단 구성하고, 그 위로 구성한 것을 볼 수 있다.

수식트리 구성과정

수식트리의 구성과정은 다음과 같다

• 수식 트리에 사용할 연산자와 피연산자를 모두 각각 노드로 만든다.
• 피연산자가 나올때까지 연산자를 스택에 담는다.
• 피연산자가 나오면 피연산자를 루트 노드로 하는 트리를 구성한다.
• 구성한 트리는 다시 스택에 담는다.
  • 루트 노드만 스택에 담으면 트리가 스택에 담긴다
• 위 과정을 계속 반복해 최종적으로 수식 트리를 구성한다.

수식트리 구성 코드

BTreeNode *MakeEXPTree(char exp[])
{
   Stack stack;
   BTreeNode *pnode;

   int expLen = strlen(exp);
   int i;

   StackInit(&stack);

   for (i = 0; i < expLen; i++)
   {
      pnode = MakeBTreeNode();

      if (isdigit(exp[i]))
      {
         SetData(pnode, exp[i] - '0');
      }
      else
      {
         MakeRightSubTree(pnode, SPop(&stack));
         MakeLeftSubTree(pnode, SPop(&stack));
         SetData(pnode, exp[i]);
      }

      SPush(&stack, pnode);
   }

   return SPop(&stack);
}

수식 트리의 순회

수식 트리의 장점은 순회를 통해 다양한 표기법으로 수식 표현이 가능하다.

• 전위 순회하여 데이터를 출력하면 전위 표기법의 수식
• 중위 순회하여 데이터를 출력하면 중위 표기법의 수식
• 후위 순회하여 데이터를 출력하면 후위 표기법의 수식

수식 트리 순회 코드

수식 트리의 순회 코드는 다음과 같다

void ShowPrefixTypeExp(BTreeNode * bt);
void ShowInfixTypeExp(BTreeNode * bt);
void ShowPostfixTypeExp(BTreeNode * bt);

이 함수는 앞서 이진 트리를 만들때 사용한 함수들을 그대로 사용한다.

typedef void (*VisitFuncPtr)(BTData data);
void PreorderTraverse(BTreeNode * bt, VisitFuncPtr action);
void InorderTraverse(BTreeNode * bt, VisitFuncPtr action);
void PostorderTraverse(BTreeNode * bt, VisitFuncPtr action);

함수 포인터에 들어가는 함수는 다음과 같이 정의한다.

void ShowNodeData(int data)
{
	if(0 <= data && data <= 9)
    	printf("%d ", data);
    else
    	printf("%c ", data);
}

전체 코드

실행에 필요한 파일은

• 이진트리
• 스택
• 수식트리
• 메인함수

메인함수를 제외하면.h, .c 각각 두 가지씩 총 7개의 파일이 필요하다.

또한 스택 헤더파일의 typedef선언을 typedef BTreeNode * Data;로 변경해야 한다.

헤더파일

#ifndef __EXPRESSION_TREE_H__
#define __EXPRESSION_TREE_H__

#include "BinaryTree2.h"

BTreeNode *MakeEXPTree(char exp[]); // 수식 트리 구성
int EvaluateExpTree(BTreeNode *bt); // 수식 트리 계산

void ShowPrefixTypeExp(BTreeNode *bt);  // 전위 표기법 기반 출력
void ShowInfixTypeExp(BTreeNode *bt);   // 중위 표기법 기반 출력
void ShowPostfixTypeExp(BTreeNode *bt); // 후위 표기법 기반 출력

#endif

소스파일

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <ctype.h>
#include "ListBaseStack.h"
#include "BinaryTree2.h"

BTreeNode *MakeEXPTree(char exp[])
{
   Stack stack;
   BTreeNode *pnode;

   int expLen = strlen(exp);
   int i;

   StackInit(&stack);

   for (i = 0; i < expLen; i++)
   {
      pnode = MakeBTreeNode();

      if (isdigit(exp[i]))
      {
         SetData(pnode, exp[i] - '0');
      }
      else
      {
         MakeRightSubTree(pnode, SPop(&stack));
         MakeLeftSubTree(pnode, SPop(&stack));
         SetData(pnode, exp[i]);
      }

      SPush(&stack, pnode);
   }

   return SPop(&stack);
}

int EvaluateExpTree(BTreeNode *bt)
{
   int op1, op2;

   if (GetLeftSubTree(bt) == NULL && GetRightSubTree(bt) == NULL)
      return GetData(bt);

   op1 = EvaluateExpTree(GetLeftSubTree(bt));
   op2 = EvaluateExpTree(GetRightSubTree(bt));

   switch (GetData(bt))
   {
   case '+':
      return op1 + op2;
   case '-':
      return op1 - op2;
   case '*':
      return op1 * op2;
   case '/':
      return op1 / op2;
   }

   return 0;
}

void ShowNodeData(int data)
{
   if (0 <= data && data <= 9)
   {
      printf("%d ", data);
   }
   else
   {
      printf("%c ", data);
   }
}

void ShowPrefixTypeExp(BTreeNode *bt)
{
   PreorderTraverse(bt, ShowNodeData);
}

void ShowInfixTypeExp(BTreeNode *bt)
{
   InorderTraverse(bt, ShowNodeData);
}

void ShowPostfixTypeExp(BTreeNode *bt)
{
   PostorderTraverse(bt, ShowNodeData);
}

메인파일

#include <stdio.h>
#include "ExpressionTree.h"

int main()
{
   char exp[] = "32+7*";
   BTreeNode *eTree = MakeEXPTree(exp);

   printf("전위 표기법의 수식 : ");
   ShowPrefixTypeExp(eTree);
   printf("\n");

   printf("중위 표기법의 수식 : ");
   ShowInfixTypeExp(eTree);
   printf("\n");

   printf("후위 표기법의 수식 : ");
   ShowPostfixTypeExp(eTree);
   printf("\n");

   printf("연산의 결과 : %d \n", EvaluateExpTree(eTree));

   return 0;
}