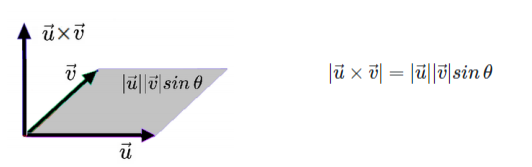---

🖋 Chapter 01. 벡터(Vector)

---

🖋 1. 벡터의 정의와 표기법

벡터란?

• 벡터라는 단어는 라틴어에서 비롯되었다.
• 벡터는 크기와 방향을 모두 가지는 양으로, 위치, 속도, 힘 등을 나타낼 수 있다.
• 물리학 및 공학에서는 유클리드 벡터, 기하 벡터, 공간 벡터 등으로 불린다.
• 크기만을 가지는 양을 스칼라라고 한다.

벡터의 표기법

• 한 벡터를 나타낼 때, 보통 $\mathbf{a}$, $\vec{a}$, $\tilde{a}$ 등으로 표기한다.
• 벡터의 크기만을 나타낼 때는 $|a|$ 또는 $a$ 로 표기한다.
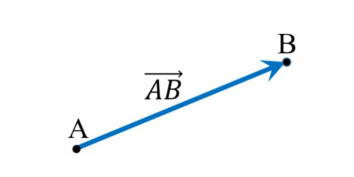
• 점 A에서 점 B를 향하는 벡터는 $\overrightarrow{AB}$ 로 나타낸다.
• A를 화살표의 원점, 기점, 꼬리라고 하며 B는 화살표의 끝, 종점, 머리라고 표현한다.

---

🖋 2. 벡터의 기본적인 성질

동등성

• 벡터는 크기와 방향만을 가지므로 원점의 특정한 위치는 아무런 의미를 갖지 않는다. 즉, 원점이 일치하지 않더라도 두 화살표의 방향이 일치하고 그 크기가 같으면 동일한 벡터이다.

영 벡터

• 영벡터는 크기가 영인 벡터를 의미한다.

음 벡터

• 벡터 $\mathbf{a}$ 자신에 더했을 때 결과가 영벡터가 되는 벡터를 $\mathbf{a}$의 음벡터라고 정의하며, $-\mathbf{a}$로 표시한다. 음 벡터 $-\mathbf{a}$는 $\mathbf{a}$와 크기는 같으나 방향이 정반대인 벡터이다.

벡터의 좌표와 성분

• 벡터를 표현하는 방법으로 공간에 좌표계를 설정하여 좌표 값을 사용할 수 있다.
• 가장 흔한 예로는 직각좌표계를 사용한다. 한 벡터의 기점을 좌표계의 원점으로 하고 벡터의 종점의 좌표로 해당 벡터를 표시한다.

단위 벡터

• 벡터의 성분 표시를 편리하게 하기 위해 추가적인 단위 벡터를 도입할 수 있다.
• 단위 벡터는 크기가 1이며, 특정한 방향을 갖는 벡터이다. 벡터의 방향을 나타내기 위해 사용될 뿐 차원과 단위가 없다.
• 3차원의 직각좌표계 $(X, Y, Z)$가 주어질 때, 각 좌표축에 나란한 방향을 갖는 단위벡터를 각각 $\hat{i}$, $\hat{j}$, $\hat{k}$ 라고 나타낸다.
• 모든 좌표축에 대한 단위 벡터들의 집합 $\{\hat{i}, \hat{j}, \hat{k}\}$을 기저벡터 집합이라고 부른다.
• 특정 기저벡터 집합을 선택하는 것은 특정한 직각좌표계를 선택하는 것과 동등하다.
• 스칼라 배(Scalar multiplication)의 정의를 이용하여 벡터 $\mathbf{a}$의 성분 벡터들은 각각 아래와 같이 표현할 수 있다.
• $\mathbf{a} = a_x \hat{i} + a_y \hat{j} + a_z \hat{k}$ 또는 $\mathbf{a} = (a_x, a_y, a_z)$

---

벡터의 성분, 분해, 합성

• 벡터의 성분은 각각의 좌표축에 벡터를 투영시켜 얻는다. 이를 성분벡터(Component vector, $a_x, a_y$)라고 부른다.
• 따라서, $a_x, a_y$는 "벡터 a의 축 성분벡터"라고 부른다.
• 이것은 2차원 이상의 공간에서는 차원의 수만큼 성분이 존재하며, 차원을 확장하여 적용 가능하다.
• 벡터 $\mathbf{a}$는 $a = a_x + a_y$로 표현이 가능하다.
• 한 벡터를 자신의 성분벡터들의 합으로 나타내는 것이 벡터의 분해이다.

---

🖋 3. 벡터의 연산

벡터의 덧셈

• 기하학적인 방법 1: 삼각형법 (Tail-to-tip method)
• 기하학적인 방법 2: 평행사변형법 (Parallelogram method)
• 성분을 이용한 대수적인 방법:
  • 두 벡터 $\mathbf{a} = (a_x, a_y)$와 $\mathbf{b} = (b_x, b_y)$가 있다면, 벡터 $\mathbf{r} = (r_x, r_y)$는 $\mathbf{r} = \mathbf{a} + \mathbf{b}$이며, 각 성분별로 $r_x = a_x + b_x$, $r_y = a_y + b_y$가 된다.

벡터의 뺄셈

• 벡터 $\mathbf{a}$와 크기는 같고 방향이 정반대인 음벡터 $-\mathbf{a}$의 정의를 이용한다.
• $\mathbf{r} = \mathbf{a} - \mathbf{b}$의 양쪽에 $\mathbf{b}$를 더한 후 결합법칙과 교환법칙을 적용하여 연산의 순서를 정리하면, $\mathbf{a} = \mathbf{b} + \mathbf{r}$을 얻을 수 있다.

벡터의 곱셈

벡터의 내적 (Inner Product)

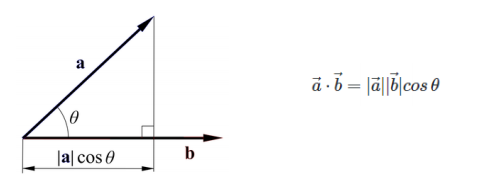
• 내적의 결과는 스칼라이다.
• 두 벡터 $\mathbf{a}$와 $\mathbf{b}$의 내적은 $a \cdot b = |a||b|\cos\theta$로 정의된다.
• 예: $\mathbf{a} \cdot \mathbf{b} = (a_x, a_y) \cdot (b_x, b_y) = a_x b_x + a_y b_y$

벡터의 외적 (Outer Product)

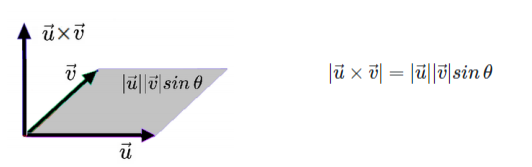
• 외적의 결과는 벡터이다.
• 두 벡터 $\mathbf{a}$와 $\mathbf{b}$의 외적은 $a \times b = |a||b|\sin\theta$로 정의된다.
• 예: $\mathbf{a} \times \mathbf{b} = (a_x, a_y, a_z) \times (b_x, b_y, b_z)$

---

🖋 4. 벡터 연산 문제

문제 1

벡터 $\mathbf{a} = (2, 3)$과 벡터 $\mathbf{b} = (4, 1)$의 합을 구하시오.

정답

$\mathbf{a}$ + $\mathbf{b} = (2 + 4, 3 + 1) = (6, 4)$

---

문제 2

벡터 $\mathbf{a} = (5, -2)$와 벡터 $\mathbf{b} = (3, 6)$의 차를 구하시오.

정답

$\mathbf{a} - \mathbf{b}$ = $(5 - 3, -2 - 6) = (2, -8)$

---

문제 3

벡터 $\mathbf{a} = (1, 2, 3)$과 벡터 $\mathbf{b} = (4, 5, 6)$의 내적을 구하시오.

정답

$\mathbf{a} \cdot \mathbf{b} = 1 \cdot 4 + 2 \cdot 5 + 3 \cdot 6 = 4 + 10 + 18 = 32$

---

문제 4

벡터 $\mathbf{a} = (2, 3, 1)$과 벡터 $\mathbf{b} = (1, -1, 4)$의 외적을 구하시오.

정답

$\mathbf{a} \times \mathbf{b} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 2 & 3 & 1 \\ 1 & -1 & 4 \end{vmatrix} = \mathbf{i}(3 \cdot 4 - 1 \cdot (-1)) - \mathbf{j}(2 \cdot 4 - 1 \cdot 1) + \mathbf{k}(2 \cdot (-1) - 3 \cdot 1) = \mathbf{i}(12 + 1) - \mathbf{j}(8 - 1) + \mathbf{k}(-2 - 3) = \mathbf{i}(13) - \mathbf{j}(7) + \mathbf{k}(-5) = (13, -7, -5)$

---

문제 5

벡터 $\mathbf{a} = (0, 4)$의 크기를 구하시오.

정답

$|\mathbf{a}| = \sqrt{0^2 + 4^2} = \sqrt{16} = 4$

---

문제 6

벡터 $\mathbf{a} = (3, 4, 5)$의 단위 벡터를 구하시오.

정답

$|\mathbf{a}| = \sqrt{3^2 + 4^2 + 5^2} = \sqrt{9 + 16 + 25} = \sqrt{50} = 5\sqrt{2}$
$\hat{\mathbf{a}} = \frac{\mathbf{a}}{|\mathbf{a}|} = \left(\frac{3}{5\sqrt{2}}, \frac{4}{5\sqrt{2}}, \frac{5}{5\sqrt{2}}\right) = \left(\frac{3}{5\sqrt{2}}, \frac{4}{5\sqrt{2}}, \frac{1}{\sqrt{2}}\right)$

---

문제 7

벡터 $\mathbf{a} = (1, 2, 3)$과 벡터 $\mathbf{b} = (4, -5, 6)$의 합을 구하시오.

정답

$\mathbf{a} + \mathbf{b} = (1 + 4, 2 - 5, 3 + 6) = (5, -3, 9)$

---

문제 8

벡터 $\mathbf{a} = (-3, 7)$과 벡터 $\mathbf{b} = (2, -8)$의 차를 구하시오.

정답

$\mathbf{a} - \mathbf{b} = (-3 - 2, 7 - (-8)) = (-5, 15)$

---

문제 9

벡터 $\mathbf{a} = (0, 1, 2)$와 벡터 $\mathbf{b} = (3, 4, 0)$의 내적을 구하시오.

정답

$\mathbf{a} \cdot \mathbf{b} = 0 \cdot 3 + 1 \cdot 4 + 2 \cdot 0 = 0 + 4 + 0 = 4$

---

문제 10

벡터 $\mathbf{a} = (2, 3)$와 벡터 $\mathbf{b} = (-1, 4)$의 외적을 구하시오 (외적은 2차원 벡터의 경우 z축 방향으로만 존재).

정답

$\mathbf{a} \times \mathbf{b} = 2 \cdot 4 - 3 \cdot (-1) = 8 + 3 = 11$

---