행렬 방정식은 벡터 방정식으로 변환이 가능하다.
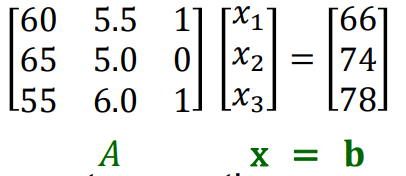
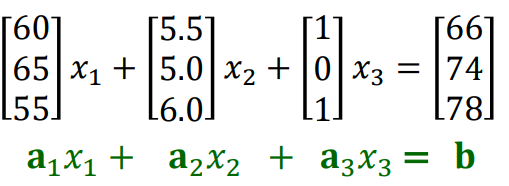
Span : 유한한 개수의 벡터들의 선형결합으로 나타낼 수 있는 모든 벡터의 집합
v3가 v3 = 2v1+3v2 와 같은 선형결합으로 표현된다면 이는 v3가 해당 평면안에 표현되며 span안에 v3가 포함된다는 것을 의미
결과적으로 선형종속은 span을 증가시키지 못하고 span(v1,v2)와 동일해짐
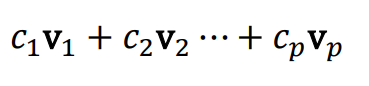
평면 상에 존재하는 모든 점들의 집합
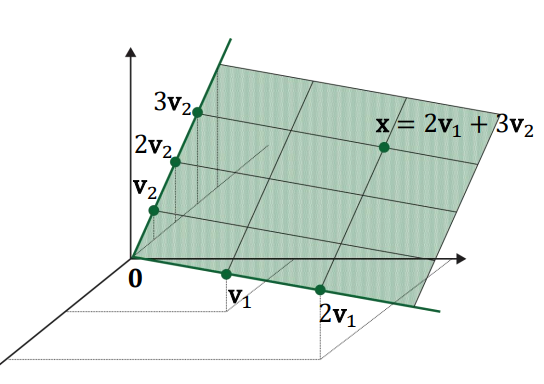
방정식의 개수 = 차원
미지수의 개수 = span의 재료벡터의 개수
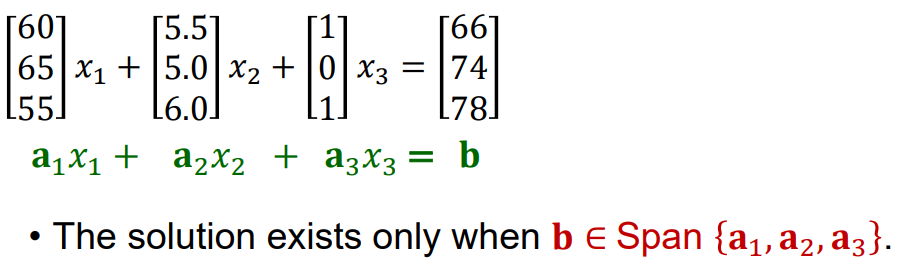


선형 독립
V1..Vn의 벡터중 하나인 Vj가 이전 벡터들의 선형결합으로 표현되지 않는 경우
x1V1+x2V2+...+xnVn = 0을 만족하는 해인 x1,...xn이 모두 0인 경우
선형방정식의 해가 유일
선형 종속
V1..Vn의 벡터중 하나인 Vj가 이전 벡터들의 선형결합으로 표현되는 경우
x1V1+x2V2+...+xnVn = 0을 만족하는 해인 x1,...xn 중 0이 아닌 xi가 존재하는 경우
선형방정식의 해가 여러개 존재
부분공간, 기저, 열공간
부분공간
부분공간(Subsapce)는 선형 결합에 닫혀있는 벡터공간 R^n의 부분집합이다. 여기서 선형결합에 닫혀있다는 의미는 Subspace 내 벡터들이 선형결합을 통해서 새로운 벡터를 만들어내도 그 벡터는 Subspace안의 또 다른 벡터라는 의미다.
기저(basis)와 차원
기저는 2가지 조건을 만족하는 부분공간 벡터들의 집합이다. 첫 번째는 해당 벡터들의 Span으로 부분공간 전체를 표현 가능(Fully Span)해야한다. 두 번째는 기저의 모든 재료 벡터들은 선형 독립이어야 한다. 부분공간 전체를 Fully Span 하는 선형 독립인 벡터의 조합은 여러개가 있을 수 있기 때문에 기저는 유일하지 않다. 하지만 기저를 구성하는 벡터의 개수는 유일하다. 여기서 기저를 구성하는 벡터의 개수를 차원이라고 정의한다.
열 공간, Rank
열 공간(Column Space)는 행렬의 열 벡터(Column Vector)를 선형결합하여 얻어지는 벡터 공간을 의미한다. 또한, 여기서 계수(Rank)는 해당 열 공간의 차원을 의미하는데 즉, 열 공간에서 기저를 구성하는 벡터들의 개수를 의미한다고 할 수 있다.
