[CS229] 2 - Linear Regression and Gradient Descent

Spark·2025년 5월 17일

CS229

목록 보기

2/3

다룰 내용들

Linear regression
LMS algrithm
Normal equation
Probabilistic interpretation
Locally weighted linear regression

Introduction

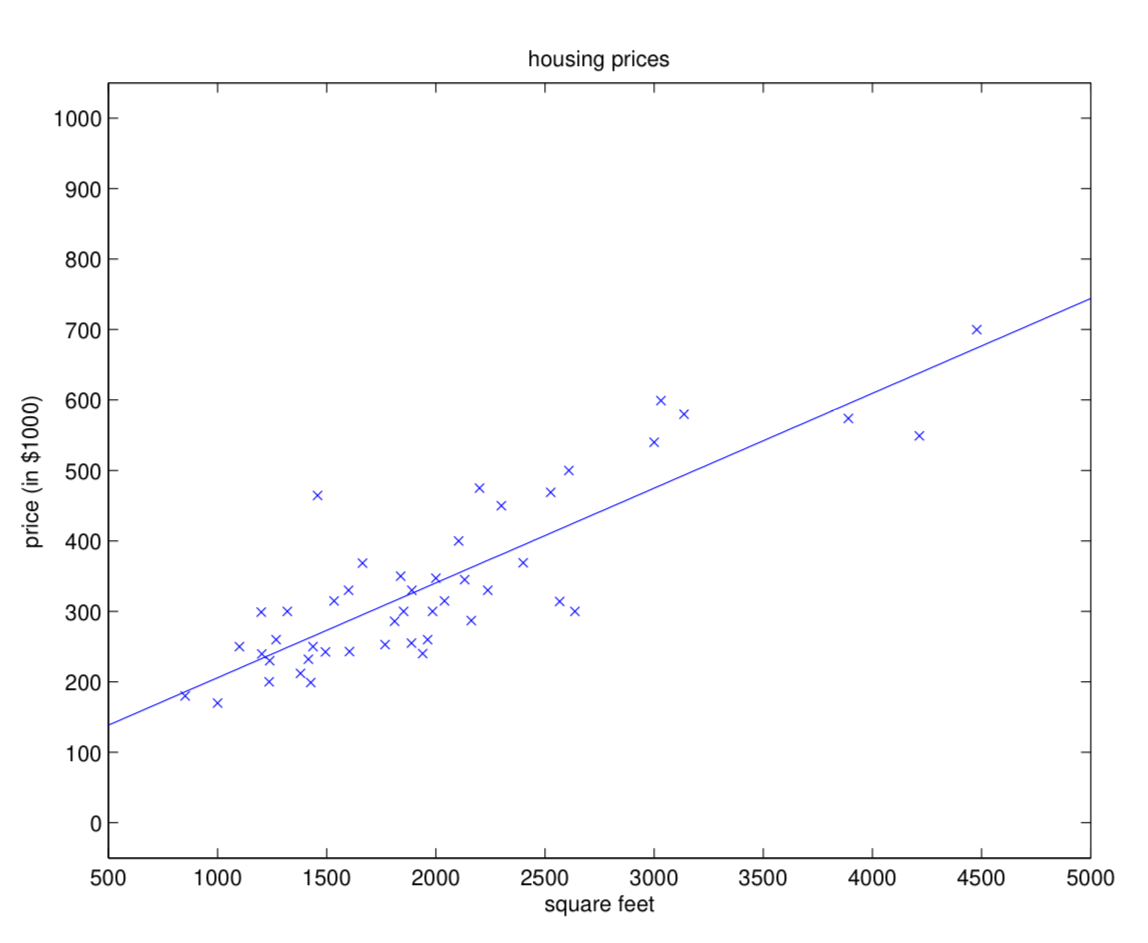
Linear regression (선형회귀)는 데이터가 산개되어 있을 때, 그 데이터를 잘 예측하는 선을 그려보자는 아이디어입니다.

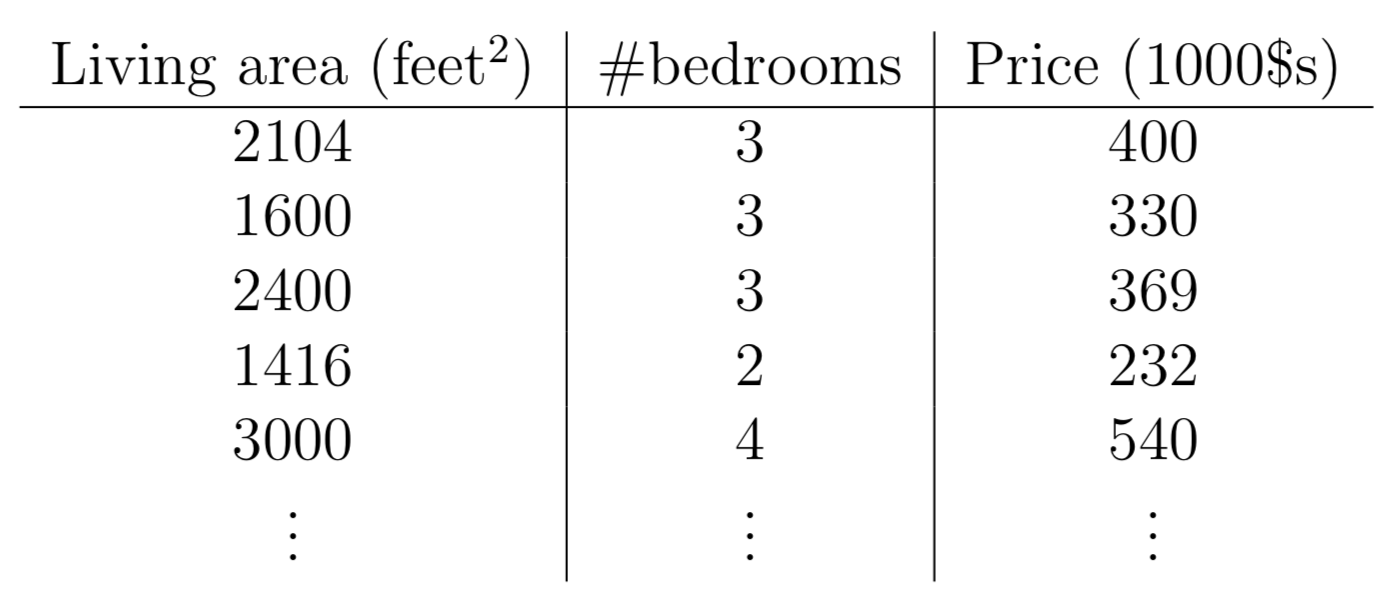
위와 같은 주거 데이터가 주어질 때, 저희가 Living area ( $x_1^{(i)}$ )와 # bedrooms ( $x_2^{(i)}$ )를 사용해서 Price를 예측해보고 싶다고 합시다.

즉, 집의 크기와 침실의 수가 입력되면, 집의 가격이 띡 나오는 식을 작성하고 싶다는 것이고, 우리는 이 식을 가설 $h$ (hypothesis)라고 합니다. 그러면, $x$ 와 가설의 관계식을 만들 수 있습니다:

h_\theta(x) = \theta_0 + \theta_1x_1 + \theta_2x_2

$\theta_j$ 는 parameter (a.k.a. weights)라고 불립니다. 우리는 이 선형 함수를 통해서, $\mathcal{X}$ 의 입력에서 $\mathcal{Y}$ 로의 매핑이 가능해집니다. $\theta_0$ 은 bias 입니다.

이를 matrix form으로 바꿔봅시다:

h(x) = \sum_{i=0}^d \theta_ix_i = \theta^Tx, \\ \theta =\begin{bmatrix} \theta_0 \\ \theta_1 \\ \vdots \\ \theta_d\end{bmatrix}, x =\begin{bmatrix} x_0 \\ x_1 \\ \vdots \\ x_d\end{bmatrix}, \text{where } x_0 = 1.

우리의 목표는 이 $h_\theta(x^{(i)})$ , i번째 데이터가 $y^{(i)}$ 를 잘 예측하도록 만들어야합니다. 즉, 우리의 cost function은 아래와 같이 정의됩니다:

J(\theta) = \frac{1}{2}\sum_{i=1}^{n}(h_\theta(x^{(i)})-y^{(i)})^2

⚠️ 강의에서는 n이 m으로 치환되어서 사용되었으나 Ng 교수님의 갈대 같은 마음에 lecture note의 term은 반대가 되었습니다. 혼동되지 맙시다!

또한, $h(x)$ 와 $h_\theta(x)$ 는 같은 의미를 담고 있습니다.

이를 LMS (least mean sqaures)이라고 정의합니다.

아무튼, 저희는 이 cost function을 사용해서 ordinary least squares regression model로 정의가 가능합니다.

1.1) LMS algorithm

저희의 목표는 $x$ 를 사용해서 $y$ 의 값을 예측하는 것이고, 이를 위한 parameter $\theta_j$ 들을 최적으로 맞추는데, 바로 $J(\theta)$ 를 사용한다고 했습니다. 그렇다면 어떻게 이를 사용할까요? 바로 gradient descent (경사하강법)을 사용할 수 있습니다:

\theta_j := \theta_j - \alpha \frac{\partial}{\partial \theta_j}J(\theta)

$\theta_j$ : j번째 데이터 특성 (j=1일경우 living area 등)
$\alpha$ : learning rate, 0.01이 good starting point

gradient를 구해봅시다:

\begin{aligned} \frac{\partial}{\partial \theta_j}J(\theta) &= \frac{\partial}{\partial \theta_j} \frac{1}{2} (h_\theta(x) - y)^2 \\ &= 2 \cdot \frac{1}{2}(h_\theta(x)-y) \cdot \frac{\partial}{\partial \theta_j}(h_\theta(x)-y) \\ &= (h_\theta(x)-y) \cdot \frac{\partial}{\partial \theta_j} \left( \sum_{i=0}^{d} \theta_ix_i - y\right) \\ &= (h_\theta(x)-y)x_j \end{aligned}

이를 통해 LMS algorithm을 작성할 수 있습니다.

$\text{Repeat until convergence \{}$

\text{} \\ \theta_j := \theta_j - \alpha \sum_{i=1}^{n}(y^{(i)}-h_\theta(x^{(i)}))x_j^{(i)},(\text{for every } j)

$\}$
Vector form으로 작성하면 아래와 같이 바뀝니다:

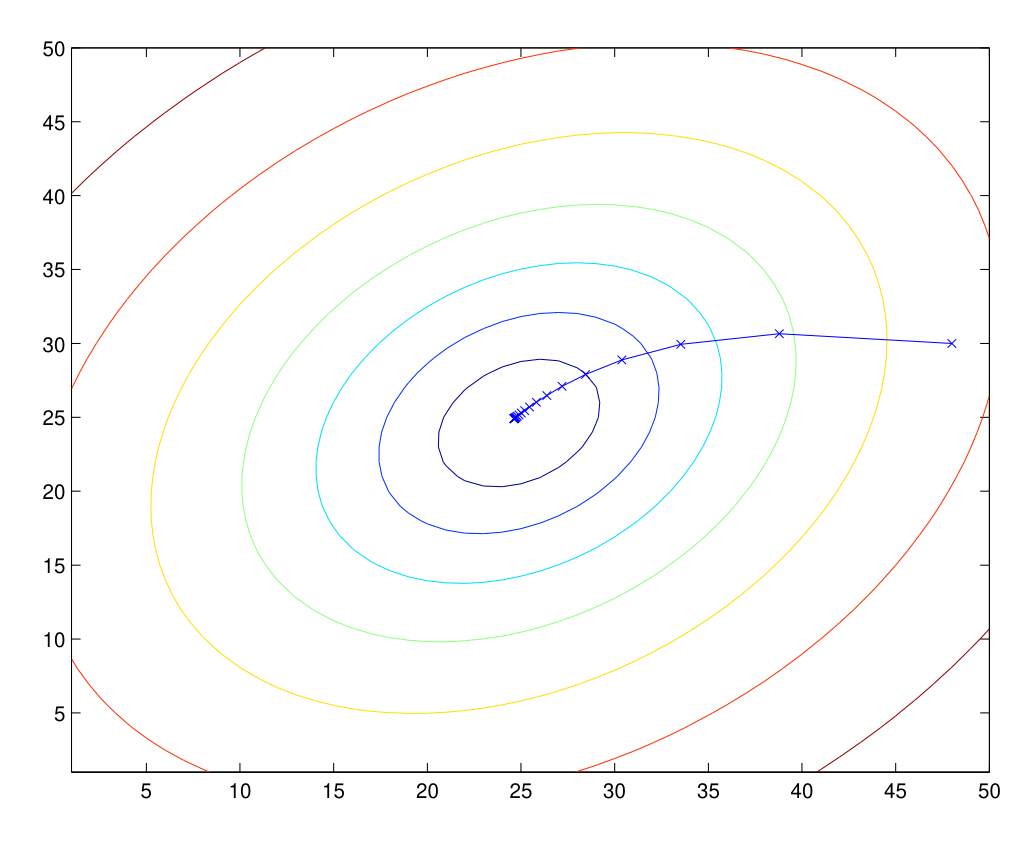
\theta := \theta - \alpha \sum_{i=1}^{n}(y^{(i)}-h_\theta(x^{(i)}))x^{(i)}

이를 batch gradient descent라고 하며, 한번의 경사 업데이트를 위해 모든 데이터가 사용된다는 것이 특징입니다.

$J(\theta)$ 는 convex parabolic function인데, 그렇기에 언제나 local minima가 global minima임이 성립합니다. LMS를 사용하는 Linear Regression 문제는, 우리가 잘 구해둔 gradient는 언제나 global minima로의 수렴으로 이어진다는 좋은 뜻이 됩니다.

우리가 각 step마다 구한 gradient는 x 기호로 표시됩니다.
또한, 이렇게 최적화된 $\theta$ 들을 통한 linear regresison은 아래와 같습니다.

다 좋은데, 문제는 하나의 업데이트, step을 밟기 위해서 모든 데이터셋이 필요하다는 점입니다. 만약에 데이터가 아주아주 많을 경우, 골치 아파지겠죠. 이를 해결하기 위해, 데이터셋 안의 데이터 하나 하나마다 업데이트를 해주는 stochastic gradient descent가 있습니다.

$\text{Loop \{}$
$\qquad\text{for i =1 to n \{}$

\text{} \\ \theta := \theta - \alpha \sum_{i=1}^{n}(y^{(i)}-h_\theta(x^{(i)}))x^{(i)},(\text{for every } j)

$\qquad\}$
$\}$

한번의 업데이트마다 한 데이터를 바라보고 fit하기 때문에, 어쩌면 영영 최고의 값에 도달하지 못할 수도 있습니다. step마다 learning rate를 줄여서 minimum에 근사하도록 함으로 문제를 해결할 수 있습니다.

1.2) The normal equations

iterative algorithm이 아닌, 행렬의 곱으로 나타내어서 한번에 딱! 식을 계산해봅시다. 이를 normal equation이라고 합니다.

1.2.1) Matrix derivatives

기존의 gradient는 다음과 같이 표현 해봅시다:

\nabla_\theta J(\theta)^{(i)} = \begin{bmatrix} \frac{\partial J^{(i)}}{\partial \theta_1} \\ \frac{\partial J^{(i)}}{\partial \theta_2} \\ \vdots \end{bmatrix}

$\frac{\partial J^{(i)}}{\partial \theta_j} \\$ 부분이 i번째 term에 한정되어있지만, 이를 모든 i에 대해 만들어버린다면, 즉 가로로 각 i에 대해 펼쳐 놓는다면 한번에 계산이 가능할 수 있겠죠! 이를 위한 선행지식을 알아봅시다.

함수 $f : \mathbb{R}^{n \times d} \mapsto \mathbb{R}$ 의 $n \times n$ 행렬 $A$ 에 대한 자코비안 행렬은 아래와 같습니다:

\nabla_A f(A) = \left[ \begin{array}{cccc} \frac{\partial f}{\partial A_{11}} & \cdots & \cdots & \frac{\partial f}{\partial A_{1d}} \\ \vdots & \ddots & & \vdots \\ \vdots & & \ddots & \vdots \\ \frac{\partial f}{\partial A_{n1}} & \cdots & \cdots & \frac{\partial f}{\partial A_{nd}} \\ \end{array} \right]

만약에 $f(A) = \frac{3}{2}A_{11}+5A_{12}^2+A_{21}A_{22}$ 로 정의된다면, 자코비안 행렬은 다음과 같습니다:

\nabla_A f(A) = \left[ \begin{array}{cc} \tfrac{3}{2} & 10A_{12} \\ A_{22} & A_{21} \end{array} \right]

1.2.2) Least squares revisited

design matrix $X$ 를 만들어봅시다:

X = \begin{bmatrix} — (x^{(1)})^T — \\ — (x^{(2)})^T — \\ \vdots \\ — (x^{(n)})^T — \end{bmatrix}

$\mathbb{R}^{n \times d+1}$ 의 차원을 가지고 있는데, bias term을 포함시켜야 해서 그렇습니다.

또한, $\vec{y}$ 를 훈련 집합의 모든 정답 값들을 포함하는 $n$ -차원 벡터라고 합시다:

\vec{y} = \begin{bmatrix} y^{(1)} \\ y^{(2)} \\ \vdots \\ y^{(n)} \end{bmatrix}

이제, $h_\theta(x^{(i)}) = (x^{(i)})^T \theta$ 이므로, 다음을 쉽게 확인할 수 있습니다:

X\theta - \vec{y} = \begin{bmatrix} (x^{(1)})^T \theta \\ \vdots \\ (x^{(n)})^T \theta \end{bmatrix} - \begin{bmatrix} y^{(1)} \\ \vdots \\ y^{(n)} \end{bmatrix} = \begin{bmatrix} h_\theta(x^{(1)}) - y^{(1)} \\ \vdots \\ h_\theta(x^{(n)}) - y^{(n)} \end{bmatrix}

따라서 벡터 $z$ 에 대해 $z^T z = \sum_i z_i^2$ 임을 이용하면:

\frac{1}{2}(X\theta - \vec{y})^T(X\theta - \vec{y}) = \frac{1}{2} \sum_{i=1}^{n} (h_\theta(x^{(i)}) - y^{(i)})^2 = J(\theta)

전개해봅시다.

\begin{aligned} \nabla_\theta J(\theta) &= \nabla_\theta \frac{1}{2}(X\theta - \vec{y})^T(X\theta - \vec{y}) \\ &= \frac{1}{2} \nabla_\theta \left( (X\theta)^T X\theta - (X\theta)^T \vec{y} - \vec{y}^T (X\theta) + \vec{y}^T \vec{y} \right) \\ &= \frac{1}{2} \nabla_\theta \left( \theta^T X^T X \theta - \vec{y}^T X\theta - (X\theta)^T \vec{y} \right) \\ &= \frac{1}{2} \nabla_\theta \left( \theta^T X^T X \theta - 2 \vec{y}^T X \theta \right) \\ &= \frac{1}{2} \left( 2 X^T X \theta - 2 X^T \vec{y} \right) \\ &= X^T X \theta - X^T \vec{y} \end{aligned}

증명 중에 어려운 부분이 있다면, LLM을 사용해서 뜯어보시길 추천드립니다. (다 설명하기엔 너무 많아요!)

$J$ 를 최소화하기 위해서, 미분값을 0으로 바꾼다면, 우리의 normal equation을 구할 수 있겠죠:

X^TX\theta = X^Ty

이를 사용해서, $J(\theta)$ 를 최소화하는 $\theta$ 의 닫힌 해를 구할 수 있습니다:

\theta = (X^TX)^{-1}X^T\vec{y}

1.3) Probabilistic interpretation

이 섹션은 우리가 왜 squared error를 사용해야 하는지에 대한 답을 제시합니다.

우리가 데이터를 $\theta^Tx^{(i)}$ 로 예측한다면, 예측을 할 수 없는, 즉 unmodeled 효과를 수반합니다.
이를 $\epsilon^{(i)}$ 로 정의하면, 우리의 식은 다시 정의됩니다:

y^{(i)}=\theta^Tx^{(i)}+\epsilon^{(i)}

여기서 $\epsilon^{(i)}$ 들은 IID (independently and identically distributed)이며, $\mathcal{N}(0,\sigma^2)$ 를 따릅니다. $\epsilon^{(i)}$ 의 확률 분포는 다음과 같습니다:

p(\epsilon^{(i)}) = \frac{1}{\sqrt{2\pi}\sigma} \exp\left( - \frac{(\epsilon^{(i)})^2}{2\sigma^2} \right)

이는 다음을 의미합니다:

p(y^{(i)} | x^{(i)}; \theta) = \frac{1}{\sqrt{2\pi}\sigma} \exp\left( - \frac{(y^{(i)} - \theta^T x^{(i)})^2}{2\sigma^2} \right)

표기 $p(y^{(i)} | x^{(i)}; \theta)$ 는 $x^{(i)}$ 가 주어졌을 때 $y^{(i)}$ 의 분포를 나타내며, $\theta$ 로 파라미터화되어 있음을 의미합니다. 여기서 중요한 점은 $\theta$ 는 확률변수가 아니므로 $p(y^{(i)} | x^{(i)}, \theta)$ 와 같이 $\theta$ 에 조건을 걸지 않는다는 것입니다.

또한, $y^{(i)}$ 의 분포는 다음과 같이 정리할 수 있습니다:

y^{(i)} \sim \mathcal{N}(\theta^T x^{(i)}, \sigma^2)

$X$ 가 디자인 행렬(모든 $x^{(i)}$ 벡터와 $\theta$ 를 포함)일 때, 모든 $y^{(i)}$ 들의 확률 분포는 어떻게 될까요?

데이터의 확률은 다음과 같이 표현됩니다:

p(\vec{y} | X; \theta)

이 값은 보통 $\vec{y}$ (그리고 아마도 $X$ )의 함수로 보지만, 우리가 $\theta$ 에 대한 함수로 명시적으로 보고 싶을 때는 이를 우도 함수(likelihood function) 라고 부릅니다:

L(\theta) = L(\theta; X, \vec{y}) = p(\vec{y} | X; \theta)

각 $\epsilon^{(i)}$ 가 독립이라는 가정을 이용해서 다음과 같이 정리할 수 있습니다:

\begin{aligned} L(\theta) &= \prod_{i=1}^{n} p(y^{(i)} | x^{(i)}; \theta) \\ &= \prod_{i=1}^{n} \frac{1}{\sqrt{2\pi}\sigma} \exp\left( - \frac{(y^{(i)} - \theta^T x^{(i)})^2}{2\sigma^2} \right) \end{aligned}

이제 이 확률 모델을 바탕으로 $y^{(i)}$ 와 $x^{(i)}$ 사이의 관계를 고려할 때, $\theta$ 를 어떻게 선택하는 것이 가장 합리적일까요?

최대우도 추정법(Maximum Likelihood Estimation, MLE)의 핵심 원리는 데이터를 생성할 확률이 최대가 되도록 $\theta$ 를 선택하라는 것입니다.

즉, 우리는 $L(\theta)$ 를 최대화하는 $\theta$ 를 선택해야 합니다.
계산의 편의를 위해 $L(\theta)$ 를 직접 사용하는 것 대신, log likelihood $\ell(\theta)$ 를 사용합시다:

\ell(\theta) = \log L(\theta) \\ = \log \prod_{i=1}^{n} \frac{1}{\sqrt{2\pi} \sigma} \exp\left( - \frac{(y^{(i)} - \theta^T x^{(i)})^2}{2\sigma^2} \right) \\ = \sum_{i=1}^{n} \log \left( \frac{1}{\sqrt{2\pi} \sigma} \exp\left( - \frac{(y^{(i)} - \theta^T x^{(i)})^2}{2\sigma^2} \right) \right) \\ = n \log \frac{1}{\sqrt{2\pi} \sigma} - \frac{1}{\sigma^2} \cdot \frac{1}{2} \sum_{i=1}^{n} (y^{(i)} - \theta^T x^{(i)})^2

따라서, $\ell(\theta)$ 를 최대화하는 것은 다음을 최소화하는 것과 동일합니다:

\frac{1}{2} \sum_{i=1}^{n} (y^{(i)} - \theta^T x^{(i)})^2

이 값은 우리가 알고 있는 원래의 최소제곱 비용 함수 $J(\theta)$ 입니다. 놀랍지 않나요?
즉, 우리가 예측할 수 없는 노이즈 $\epsilon^{(i)}$ 를 포함시킬 때, 최소 제곱 회귀와 같아지는 마법이 일어납니다.
최종적으로 $\theta$ 는 $\sigma^2$ 에 의존하지 않았는데요, 즉, $\sigma^2$ 가 알려지지 않았더라도 동일한 결과에 도달하리라는 점을 보여줍니다.
이 내용은 이후에 일반화 선형 모델 (generalized linear models)을 다룰 때 다시 사용될 예정입니다.

1.4) Locally weighted linear regression (optional reading)

기존 linear regression이 parametric learning 이라고 불렸다면, LWR (Locally weighted linear regression)은 non-parametric learning이라고 불립니다. 이 차이는 파라미터의 숫자가 고정인지, 아니면 데이터의 크기에 따라 달라지는지에 따라 나뉘는데, 후자인 LWR은 데이터의 크기에 따라 파라미터의 숫자가 변하고, 그렇기에 non-parametric learning이라고 불립니다.

LWR은 $x^{(i)}$ 에 가까운 데이터들 ( $x$ 를 기준으로)을 사용해서 $\theta$ 를 fit하고, $\theta^Tx$ 를 리턴합니다.
기존 선형 회귀 모델과 비교해봅시다.

선형 회귀 모델:

$\sum_i(y^{(i)}-\theta^Tx^{(i)})^2$ 를 최소화하는 $\theta$ 학습 후에 $\theta^Tx$ 로 예측한다.

LWR

$\sum_iw^{(i)}(y^{(i)}-\theta^Tx^{(i)})^2$ 를 최소화하는 $\theta$ 학습 후에 $\theta^Tx$ 로 예측한다.

여기서 $w^{(i)}$ 는, 음수가 아닌 값의 가중치인데, i와 가까운 $x$ 일 수록 원본에 가깝게 반영되고, 멀 수록 데이터는 무시됩니다.
이 대역폭을 bandwidth라고 하며 기호로는 $\tau$ 로 표현합니다.
아래와 같이 $w^{(i)}$ 를 계산할 수 있습니다: