Tree

• 하나의 뿌리로부터 가지가 아래로 뻗어나가는 형태의 일방향 그래프
• 계층적 자료구조: 데이터가 아래로 연결되어 뻗어 나가면서 계층적으로 표현이 되고 사이클이 없다
• 비선형 구조: 하나의 데이터 뒤에 여러 개의 데이터가 존재할 수 있다
• 루트 (root): tree의 시초가 되는 꼭짓점 데이터
• 노드 (node): tree에 속한 각각의 꼭짓점 데이터
• 부모 노드 (parent node): 특정 node에 edge로 연결이 된 상위 node
• 자식 노드 (child node): 특정 node에 edge로 연결이 된 하위 node
• 레벨 (level): node와 node 사이의 간격 (root가 level 1)

(흔히 접하는 tree의 예시로 컴퓨터의 파일 관리 구조가 있다)

Binary Search Tree

이진 트리 (binary tree): 각 node 마다 최대 2개의 child node를 가질 수 있는 tree
이진 탐색 트리 (binary search tree): 모든 왼쪽 자식은 부모보다 작은 값이고, 모든 오른쪽 자식은 부모보다 큰 값인 tree (새로운 node를 추가할 때, 위의 규칙에 따라 새 node의 값을 따져 위치를 정한다)

Tree traversal

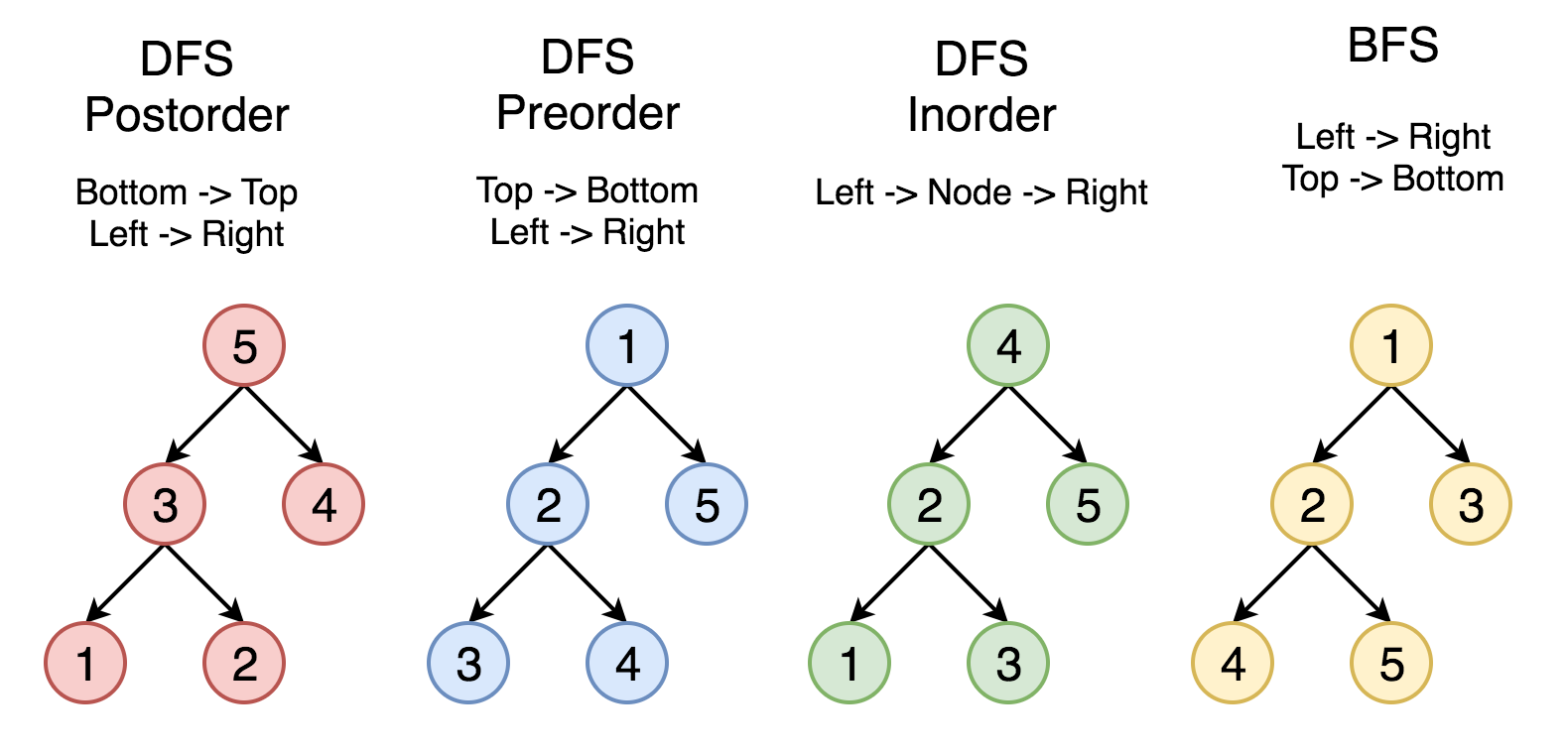
• 트리 순회 (tree traversal): 특정 목적 (예: 조건에 맞는 node를 찾기 위해) 을 위해 모든 노드를 특정 순서대로 방문하는 것
• 전위 순회 (preorder traversal): root에서 시작해 기준으로 왼쪽 node부터 탐색 후 오른쪽 node를 탐색한다 (그림에서 하늘색)
• 중위 순회 (inorder traversal): 가장 왼쪽 node에서 시작해 parent node, 오른쪽 node 순서로 탐색한다 (그림에서 초록색)
• 후위 순회 (postorder traversal): 가장 왼쪽 node에서 시작해 오른쪽 node를 탐색 후 1 level 위로 올라가 탐색한다 (그림에서 분홍색)

Heap

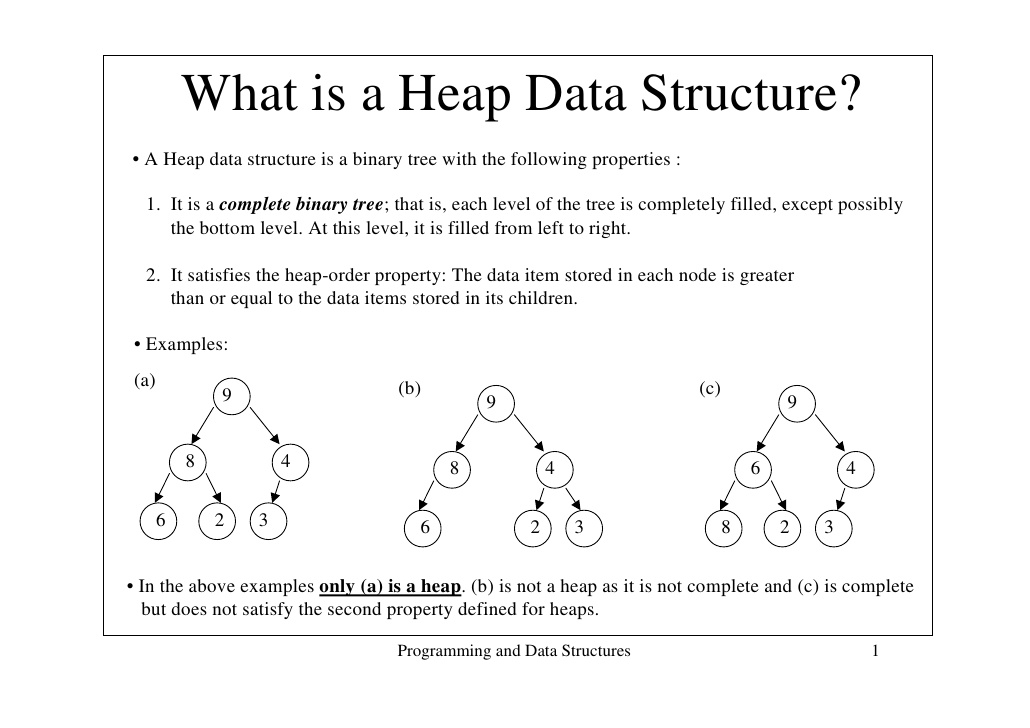
• 힙 구조 (heap): binary tree의 일종으로, (1) 가장 아래를 제외한 tree의 각 level이 채워져 있어야 하며 (2) 가장 아래 level은 전부 채워져 있지 않은 경우 왼쪽부터 순서대로 채워져 있어야 하고 (3) parent node의 값이 child node보다 커야 한다
• 그림에서 (b)는 (2)번 조건을 충족하지 않아 heap이 아니며, (c)는 (3)번 조건을 충족하지 않아 heap이 아니다 ((a)만 heap에 해당)