[TIL] Time Complexity

Time Complexity

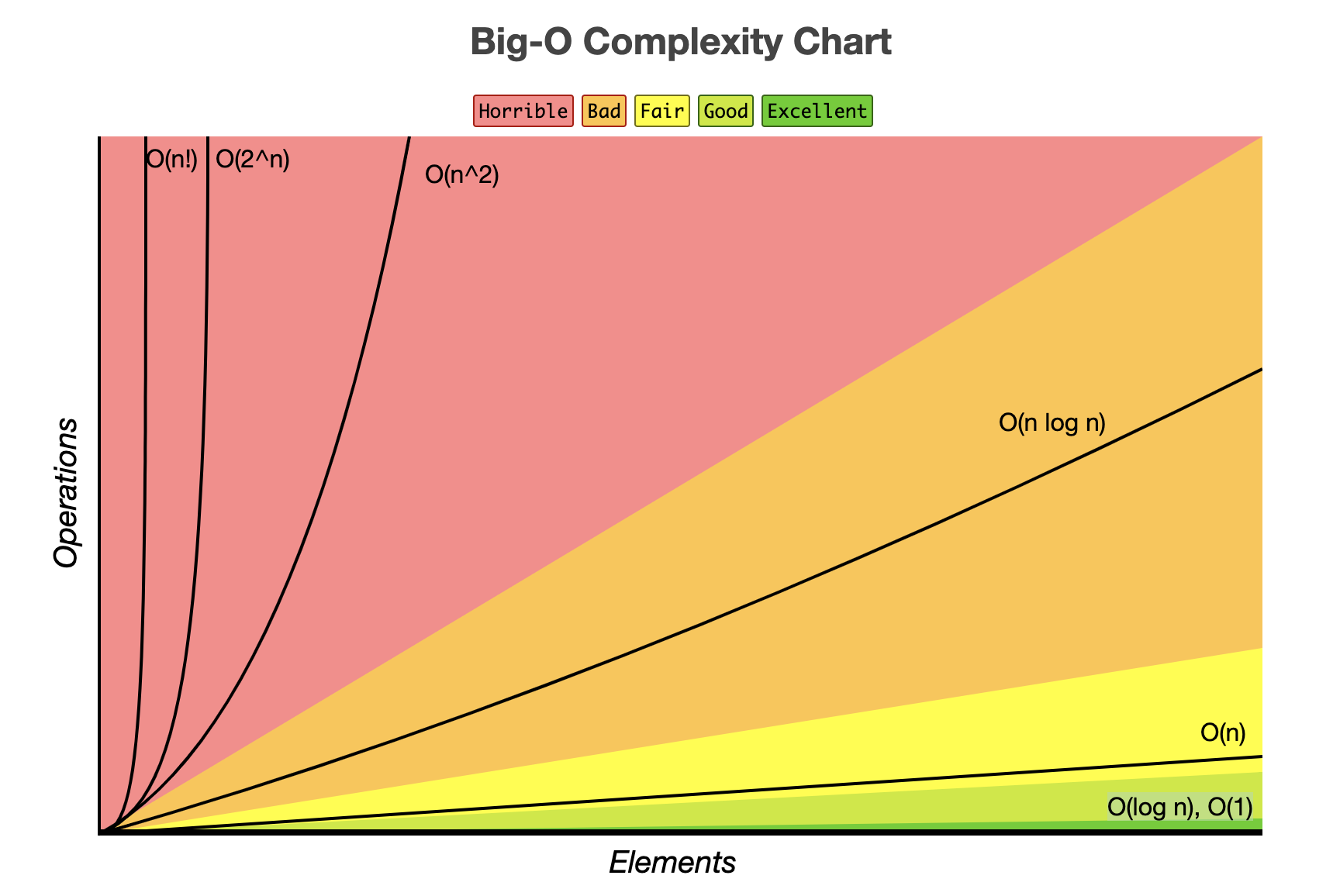
• 입력값의 증감에 따라 시간이 얼마만큼 비례하여 증감하는지 표현한 개념
• Big-O: 가능한 경우의 수 중 최악의 경우 (가장 시간이 오래 걸릴 경우)를 의미한다

O(1)

• a.k.a constant complexity
• 입력값이 증가해도 소요 시간은 늘어나지 않는다
• e.g. index값을 이용해 array의 element 조회하기

O(n)

• a.k.a linear complexity
• 소요 시간이 입력값에 정비례해서 일정 비율로 늘어난다
• time complexity가 O(n)인 알고리즘 A가 있고, 소요 시간이 늘어나는 비율이 A의 2배인 알고리즘 B가 있을 때, B의 time complexity를 O(2n)으로 표기하지 않는다 (입력값이 커질수록 계수의 영향이 작아지기 때문)
• e.g. for문 (iterable object의 길이가 1씩 늘어날 때마다 시간도 1씩 증가한다)

O(log n)

• a.k.a. logarithmic complexity
• 입력값이 늘어날수록 소요 시간이 늘어나는 비율이 작아진다 (0에 수렴)
• e.g. binary search (탐색을 1회 실행할 때마다 탐색해야 할 양이 반감된다)

O(n ^ 2)

• 입력값이 늘어날수록 소요 시간이 제곱 비율로 늘어난다
• O(n)과 같은 맥락으로, O(n ^ 3) 등은 모두 O(n ^ 2)로 표현을 통일한다
• e.g. 이중 for문 (바깥쪽 for문을 n회 실행하고, 그 n회에 대해서 각각 안쪽 for문을 n회 실행한다)

O(2 ^ n)

• a.k.a. exponential complexity
• 입력값이 늘어날수록 소요 시간이 늘어나는 비율이 커진다 (기하급수적으로 늘어남)
• e.g. 재귀로 구현한 피보나치 수열

데이터 크기 제한에 따른 예상 time complexity

• n ≤ 1,000,000: O(n) or O (log n)
• n ≤ 10,000: O(n ^ 2)
• n ≤ 500: O(n ^ 3)

Greedy Algorithm

문제를 해결하는 과정에서 그 순간에 최적이라 생각되는 해답(locally optimal solution)을 찾으며, 이를 토대로 최종 문제의 해답(globally optimal solution)에 도달하는 문제 해결 방식

3 Steps of a Greedy Algorithm

1. 선택 절차 (Selection Procedure): locally optimal solution 도출
2. 적절성 검사 (Feasibility Check): 1의 해답이 문제의 조건을 만족하는지 검사
3. 해답 검사 (Solution Check): globally optimal solution이 도출되었는지 검사 (아닌 경우 1부터 3까지 반복)

2 Conditions for a Greedy Algorithm

1. 탐욕적 선택 속성(Greedy Choice Property): 이전의 선택이 이후의 선택에 영향을 미치지 않는다
2. 최적 부분 구조(Optimal Substructure): globally optimal solution은 locally optimal solution으로 이루어져 있다

Dynamic Programming

문제를 여러 개의 하위 문제로 나누어 풀고, 하위 문제들의 해결 방법을 결합하여 최종 문제를 해결 (하나의 문제는 한 번만 풀도록 한다)

2 Conditions of Dynamic Programming

1. Overlapping Sub-problems: 하위 문제의 답은 항상 같고, 상위 문제를 해결하기 위해 여러 번 반복해서 사용될 수 있어야 한다
2. Optimal Substructure: 상위 문제의 최적의 해법은 하위 문제의 최적의 해법을 결합하여 구할 수 있어야 한다

-> e.g. 재귀로 구현한 피보나치 수열 (fib(5)를 구할 때, fib(4)와 fib(3)의 답을 통해 답을 구할 수 있어야 한다)

Top-down vs. Bottom-up

• Top-Down Dynamic Programming: Recursion + Memoization
  상위 문제에서 시작해서 하위 문제로 나눈 후에 하위 문제를 호출하여 상위 문제를 해결한다 (fib(5)를 fib(4)와 fib(3)의 합으로 나누고, fib(4)를 fib(3)과 fib(2)의 합으로 나누고...)
• Bottom-Up Dynamic Programming: Iteration + Tabulation
  하위 문제로부터 답을 쌓아 올려 상위 문제를 해결한다 (fib(0)의 해답으로부터 fib(1)을 구하고, 그로부터 fib(2)를 구하고...)