10장 RECAP
역전파 알고리즘은 출력층에서 입력층으로 오차 gradient를 전파하면서 진행된다. 알고리즘이 신경망의 모든 파라미터에 대한 오차 함수의 gradient를 계산하면, 경사 하강법 단계에서 이 gradient를 사용해서 각 파라미터를 수정한다.
11장에서는...
심층 신경망 훈련에서 발생할 수 있는 문제
- gradient 소실/폭주
- 훈련데이터 불충분, 라벨링 작업의 높은 비용
- 훈련데이터에 과적합되는 문제
Gradient 소실 / 폭주
Vanishing Gradient: 알고리즘이 하위층으로 진행될수록 gradient가 점차 감소한다. 경사하강법이 하위층의 연결 가중치를 변경되지 않은 채로 둔다면 훈련이 제대로 이뤄지지 않게 된다.
Exploding Gradient: gradient가 점차 커져서 여러 층이 비정상적으로 큰 가중치로 갱신되게 되고, 알고리즘은 발산(diverse)한다.
❔발생 원인
- logistic sigmoid 활성화 함수
- 가중치 초기화 방식 (평균: 0, 표준편차: 1 인 정규분포)
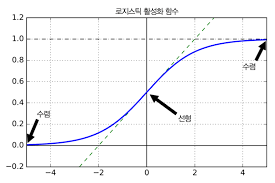 (0이나 1로 수렴할 때 기울기가 0에 수렴함. 이 때문에 역전파될 때 신경망으로 전파할 gradient가 거의 없어진다. 따라서, 실제로 하위층에는 아무것도 도달하지 않게 된다.)
(0이나 1로 수렴할 때 기울기가 0에 수렴함. 이 때문에 역전파될 때 신경망으로 전파할 gradient가 거의 없어진다. 따라서, 실제로 하위층에는 아무것도 도달하지 않게 된다.)
Glorot 초기화 & He 초기화
글로럿과 벤지오는 논문을 통해 불안정한 gradient 문제를 완화할 방법이 제안했다.
예측을 할 때는 정방향으로, 역전파할 때는 그레이디언트를 역방향으로 하여 양방향 신호가 적절하게 흘러야 한다. 논문에 따르면, 각 층의 출력에 대한 분산이 입력에 대한 분산과 같아야 하며, 역방향에서 층을 통과하기 전과 후의 그레이디언트 분산이 동일해야 한다.
층의 입력과 출력 연결 개수(각각 fan-in, fan-out이라고 부름)가 같지 않으면 위의 2가지를 보장할 수 없다. 하지만 논문 저자들은 실전에서 매우 잘 작동한다고 입증된 대안을 제안했는데, 각 층의 연결 가중치를 아래와 같이 무작위로 초기화하는 것이다. 이러한 초기화 전략을 글로럿 초기화라고 한다.

글로럿 초기화를 사용하면 훈련 속도를 상당히 높일 수 있다.
세이비어 초기화는 S자 형태의 활성화 함수(시그모이드, 하이퍼볼릭탄젠트 등)와 함께 사용할 경우 좋은 성능을 보이지만, ReLU와 함께 사용할 때는 좋지 않다. ReLU는 아래에서 이야기할 He 초기화와 함께 사용하는 것이 좋다.
일부 논문들이 다른 활성화 함수에 대해 비슷한 전략을 제안했다. ReLU 활성화 함수에 대한 초기화 전략은 He 초기화, SELU 활성화 함수에 대한 초기화는 르쿤(LuCun) 초기화를 사용한다.
각 초기화 전략의 활성화 함수 및 정규분포는 아래 표와 같다.

수렴하지 않는 활성화 함수
이전에는 시그모이드 활성화 함수가 최선의 선택이라 여겨졌지만, 기울기 소실이 발생할 수 있다는 단점 때문에 다른 활성화 함수가 심층 신경망에서 훨씬 더 잘 작동한다는 사실이 밝혀졌다.
✅ ReLU 함수: 특정 양숫값에 수렴하지 않고 계산이 빠르다는 큰 장점이 있으나, 죽은 ReLU(dying ReLU) 문제를 갖고 있다. 훈련하는 동안 일부 뉴런이 0 이외의 값을 출력하지 않는 것이다. 뉴런의 가중치가 바뀌면서 훈련 세트에 있는 모든 샘플에 대해 입력의 가중치 합이 음수가 되면 ReLU 함수의 그레이디언트가 0이 되어 경사 하강법이 더는 작동하지 않는다.
👉 LeakyReLU 사용
: 하이퍼파라미터 ɑ가 z<0일 때의 기울기를 결정하며 이 값을 작게 하는 것이 성능이 더 좋게 나타난다.
(ɑ가 새는 정도를 결정한다.)
✅ RReLU: 훈련 시 주어진 범위에서 ɑ의 값을 랜덤으로 선택, 테스트 시 평균을 사용.
✅ PReLU: ɑ가 훈련되는 동안 학습됨. 대규모 데이터셋에서는 좋은 성능을 보이나 소규모 데이터셋에서는 훈련 세트에 과대적합될 위험 존재.
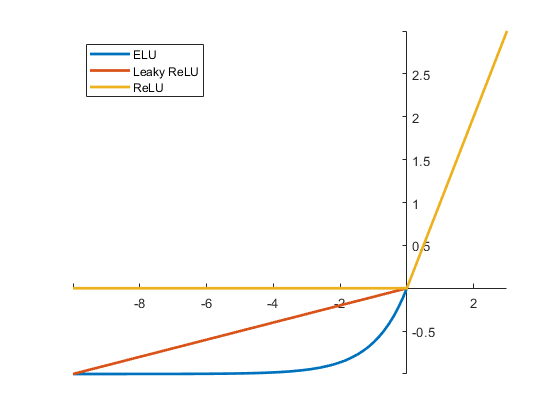
✅ ELU 활성화 함수
- 다른 ReLU 함수들의 성능을 앞지르지만, 계산이 느린 단점이 있다.
- 하이퍼파라미터 a는 z<0일 때 ELU가 수렴할 값을 정의한다.
- z<0일 때 활성화 함수의 평균 출력이 0에 더 가까워져 그레이디언트 소실 문제를 완화해준다.
- ɑ=1이면 z=0에서 급격한 변화가 일어나지 않으므로 경사 하강법의 속도가 빨라진다.
Batch Normalization
ELU와 함께 He 초기화를 사용하면 훈련 초기 단계에서 gradient 소실/폭주 문제를 감소시킬 수 있지만, 훈련 중 다시 발생하지 않으리란 보장은 없다.
이런 문제를 해결하기 위해 제안된 것이 배치 정규화(BN)기법이다. 이 기법은 각 층에서 활성화 함수를 통과하기 전이나 후에 모델에 연산을 하나 추가한다. 이 연산은 입력을 원점에 맞추고 정규화한 다음, 각 층에서 2개의 새로운 파라미터로 output의 스케일을 조정하고 이동시킨다.
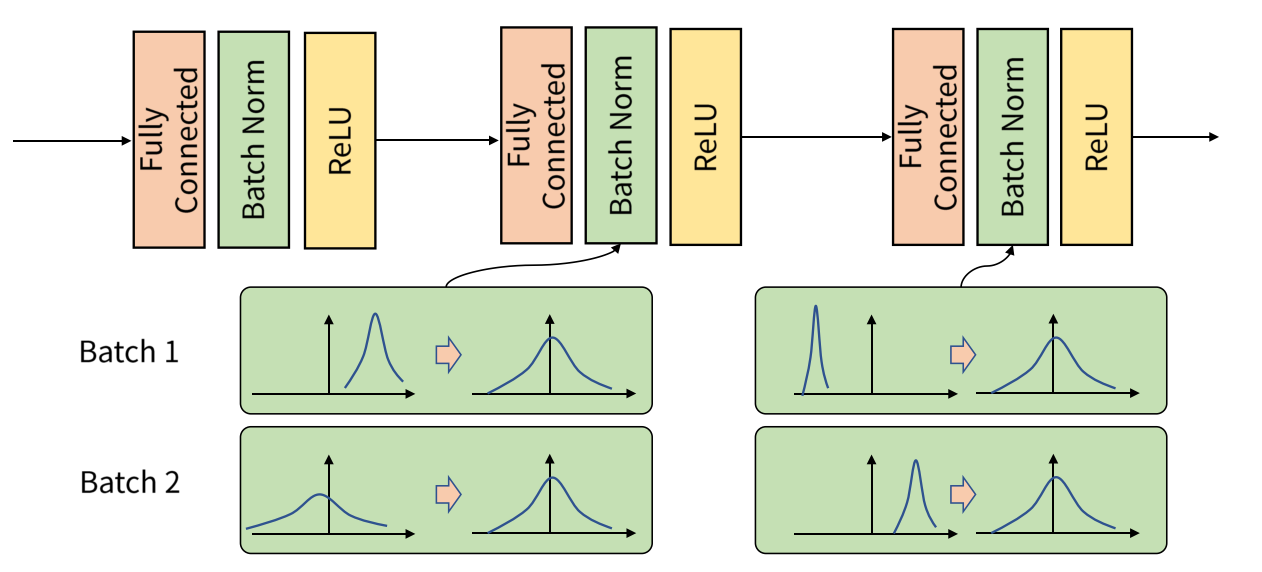
위와 같이, BN 기법은 학습 과정에서 계층 별로 데이터 분포가 달라지더라도, 각 배치별로 평균과 분산을 이용해서 정규화할 수 있다.

❗ 배치 정규화는 학습단계 / 추론단계 각각 조금씩 다르게 적용돼야 한다.
- 학습 단계의 BN을 구하기 위하여 사용된 평균과 분산을 구할 때에는, 배치별로 계산되어야 한다. 각 배치들이 표준 정규 분포를 각각 따르게 하기 위해서다.
- 추론 과정에서는 BN에 적용할 평균과 분산에 고정값을 사용합니다.
이 때 사용할 고정된 평균과 분산은 학습 과정에서 이동 평균(moving average) 또는 지수 평균(exponential average)을 통하여 계산한 값이다. 즉, 학습 하였을 때의 최근 N 개에 대한 평균 값을 고정값으로 사용하는 것이다.
batch는 gradient를 구하는 단위
Gradient Clipping
그레이디언트 폭주 문제를 완화하는 다른 방법으로, 역전파될 때 일정 임곗값을 넘어서지 못하게 그레이디언트를 잘라낸다.
사전훈련된 층 재사용하기
훈련데이터 부족할 때, 라벨링 작업의 cost가 높은 경우에 대해 해결방안이 될 수 있는 전이학습에 대해 알아보자.
해결하려는 문제와 비슷한 유형을 처리한 신경망이 있는지 보고, 있다면 그 신경망의 하위층을 재사용하는 것이 처음부터 새로 훈련하는 것보다 훨씬 효율적이다. 이런 방식을 Transfer learning(전이 학습)이라고 한다.
훈련 속도를 높일 뿐만 아니라 필요한 훈련 데이터의 양도 줄여준다.
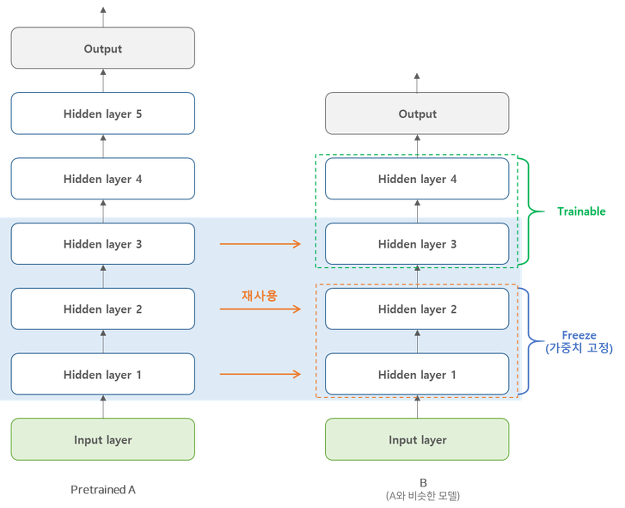
전이 학습 시 원본 모델의 출력층은 새로운 작업에서 가장 유용하지 않은 층이므로 바꿔주어야 한다. 그리고 이와 비슷하게 원본 모델의 상위 은닉층은 하위 은닉층보다 덜 유용하다. 따라서 재사용할 층의 개수를 잘 선정해야한다.
가중치가 바뀌지 않도록 재사용하는 층을 모두 동결한다. 그 다음 모델을 훈련하고 성능을 평가한다.
고속 Optimizer
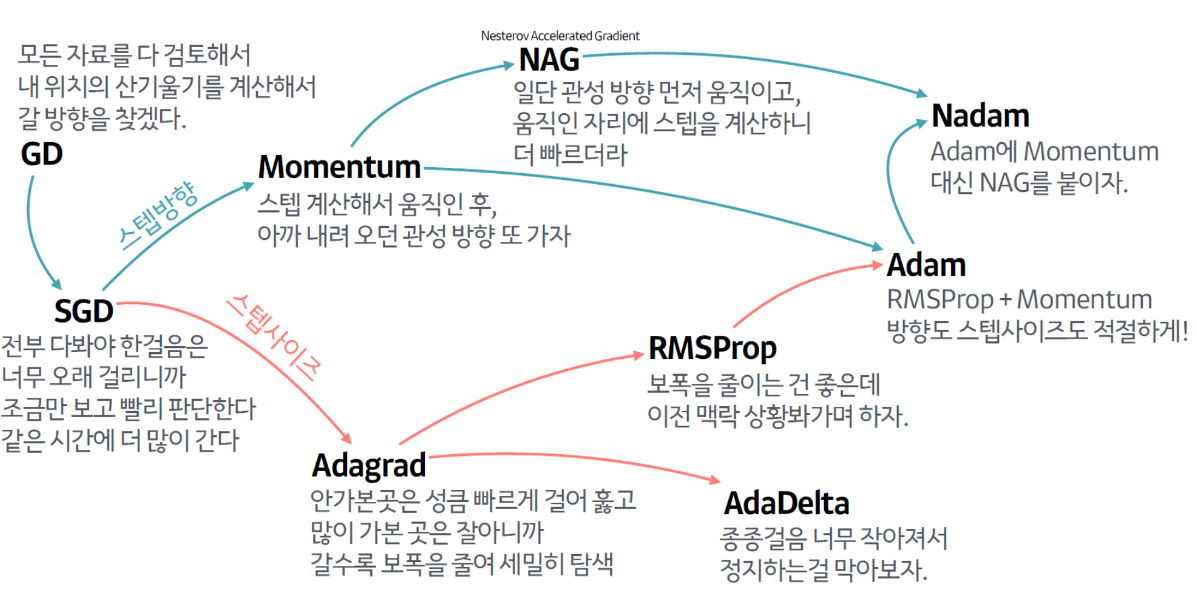
✅ 모멘텀 최적화
표준적인 경사 하강법은 경사면을 따라서 '일정한 크기의' 스텝으로 조금씩 내려가기 때문에, 최적점에(가장 아래에 있는 지점) 도착하기까지 시간이 비교적 오래 걸린다. 더불어, 이전 gradient가 얼마였는지 고려하지 않아서 gradient가 locally 작으면 매우 느려진다.
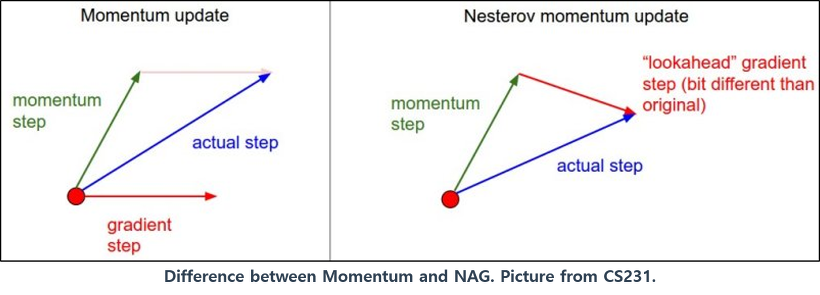
반면에, 모멘텀 최적화는 이전 gradient가 얼마였는지를 상당히 중시한다. 아래 식과 같이 매 반복에서 현재 gradient를 모멘텀 벡터에 더하고 이 값을 빼는 방식으로 가중치를 갱신한다. 즉, gradient를 속도가 아닌 '가속도'로 사용한다. 모멘텀 최적화는 골짜기를 따라 최적점에 도달할 때까지 점점 더 빠르게 내려가게 된다.
배치 정규화를 사용하지 않는 심층 신경망에서 상위층은 종종 스케일이 각기 다른 input을 받게 되는데, 모멘텀 최적화는 이런 경우에 큰 도움을 줄 수 있다. 또한 local optima를 건너뛰고 global optima로 도달할 수 있게끔 도움을 준다.


✅ 네스테로프 가속 경사
모멘텀 최적화를 변형한 형태로, 기본 모멘텀 최적화보다 거의 항상 더 빠르다. 네스테로프 가속 경사 기법은 현재 위치가 θ가 아니라, 모멘텀의 방향으로 조금 앞선 θ+βm에서 비용 함수의 gradient를 계산한다.
(원래 위치에서의 그레이디언트를 사용하는 것보다 그 방향으로 조금 더 나아가서 측정한 그레이디언트를 사용하는 것이 더 정확하다.)
✅ AdaGrad
경사 하강법은 global optima 방향으로 곧장 향하지 않고, 가장 가파른 경사를 따라 빠르게 내려가기 시작해서 골짜기 아래로 느리게 이동한다.
AdaGrad 알고리즘은 가장 가파른 차원을 따라 그레이디언트 벡터의 스케일을 감소시킨다. 이를 통해 좀 더 일찍 정확한 방향을 잡아 global optima쪽으로 향할 수 있다.
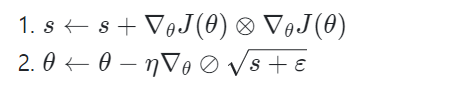
1. gradient 제곱을 벡터 s에 누적한다.
2. 경사 하강법과 거의 유사하지만, graidnet 벡터를 (s+ɛ)^(1/2)로 나누어 스케일을 조정한다.
이 알고리즘은 학습률을 감소시키지만, 경사가 완만한 차원보다 가파른 차원에 대해 빠르게 감소된다. (이를 'adaptive learning rate'라 한다.) 이로써 global optima 방향으로 비교적 곧바로 가도록 갱신되는 데 도움을 준다.
그러나, 이 알고리즘은 간단한 2차 방정식 문제에 대해선 잘 작동하지만, 신경망을 훈련할 때 학습률이 너무나도 감소해서 global optima에 도착하기 전에 알고리즘이 완전히 멈추는 문제점이 있다. 따라서 심층 신경망에는 되도록 사용하지 않는 것이 좋다. 그러나 다른 adaptive learning rate optimizer를 이해하는 데 도움을 줌으로 잘 알아두도록 하자.
✅ RMSProp(Root Mean Square Propagation)
RMSProp 알고리즘은 가장 최근 epoch에서 비롯된 gradient만을 누적함으로써 AdaGrad의 문제점을 해결했다.
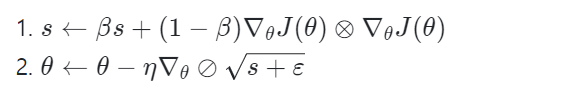
1. 지수 감소를 사용한다. 감쇠율 β라는 하이퍼파라미터가 하나 더 생겼다. (β를 튜닝할 필요까진 없음)
2. adagrad와 동일하다.
✅ Adam과 Nadam 최적화
Adam(Adaptive moment estimation): 모멘텀 최적화 + RMSProp
👉 지난 gradient의 지수 감소 평균 & 지난 gradient 제곱의 지수 감소된 평균을 따른다.
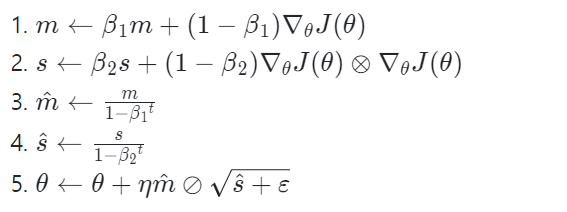
전체적으로 모멘텀 최적화와 RMSProp과 아주 비슷하다.
m과 s가 0으로 초기화되기 때문에 훈련 초기에 0쪽으로 치우치게 되어 반복 초기에 크게 기여 하지는 못한다. 따라서 단계 3,4에서 반복 초기에 m과 s를 증폭시켜주지만, 반복이 많이 진행되면 단계 3,4의 분모가 1에 가까워져서 m,s는 거의 증폭되지 않게 된다.
Adam의 변종 ➡️ AdaMax, Nadam
✅ AdaMax
Adam기법의 일종으로써 무한 노름(infinity norm)을 기반으로 한다. 그렇기 때문에 embedding같이 벡터화 기법을 사용하는 모델을 활용할 때 Adam보다 더 높은 성능을 낼 수도 있다. 기본적으로 아래 3가지 파라미터를 초기화 시켜주어야 한다.
- m = 0, 첫 번째 moment 벡터 초기화
- v = 0, 지수 가중화(exponentially weighted)되는 무한 노름의 초기화
- t = 0, timestep 초기화
Adam과의 차이점이라면, Adamax는 순방향(forward pass)에서 사용된 해당 변수 부분의 m_t, v_t 값과 slices 만을 업데이트한다. 이는 특정 변수의 slice가 실제로 사용되었을 경우를 제외하고는 momentum을 무시하는 구조라고 할 수 있다.
✅ Nadam
Adam Optimizer에 네스테로프 기법을 더한 것이다. 때때로 Adam보다 조금 더 빠르게 수렴하는 경우도 있다.
지금까지 살펴본 모든 최적화 기법은 1차 편미분(Jacobian)에만 의존한다. 최적화 이론에는 2차 편미분(Hessian)을 기반으로 한 알고리즘도 있지만, 이는 심층 신경망에 적용하기가 어려운 상황이다.
학습률 스케쥴링
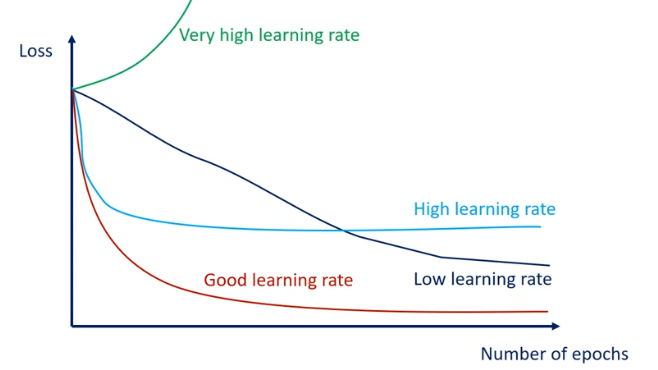
학습률은 모델 훈련에 중요한 영향을 미치는 요소다. 일정한 학습률로 모델을 훈련하는 방법도 있지만, 훈련하는 동안 학습률을 감소시키는 전략도 존재한다. 이런 전략을 학습 스케줄(learning schedule)이라고 한다.
학습 스케쥴 전략
- 거듭제곱 기반 스케줄링
- 지수 기반 스케줄링
- 구간별 고정 스케줄링
- 성능 기반 스케줄링
- 1사이클 스케줄링
Regularization를 사용해 overfitting 피하기
10장에서 이미 언급된 '조기 종료'나 '배치 정규화' 도 규제 방법으로 사용할 수 있다. 이 밖에 신경망에서 널리 사용되는 다른 규제 방법에 대해서도 알아보자.
(L1 & L2 규제, dropout, max-norm 규제)
** Regularization: 가중치 w가 작아지도록 학습시킴 -> local noise에 영향을 덜 받도록 하기 위함
✅ L1 & L2 Regularization
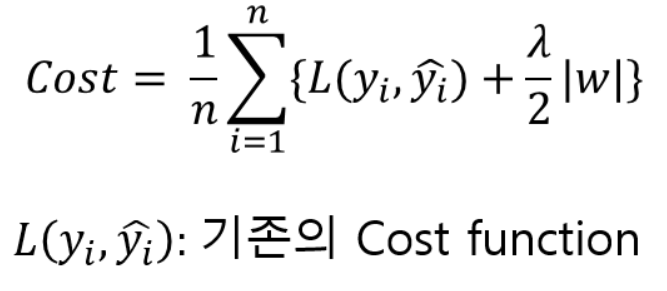
cost function에 가중치의 절댓값을 더해주는 것이 핵심이다. 기존의 cost function에 가중치의 크기가 포함되면서, 가중치가 너무 크지 않은 방향으로 학습되도록 한다. 이때 learning rate 람다 값이 0에 가까울수록 정규화의 효과가 줄어든다.
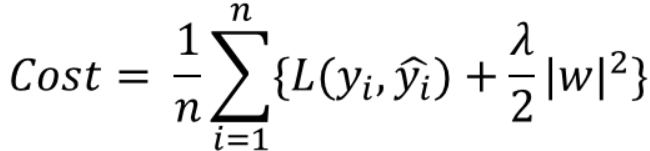
cost function에 가중치의 제곱을 더함으로써 L1 규제와 마찬가지로 가중치가 너무 크지 않은 방향으로 학습된다. 이를 weight decay라고 한다.
✅ Dropout
신경망의 크기가 커질 경우 overfitting 문제를 피하기 위한 방법
dropout은 아래 그림 (a)에 대한 학습을 할 때, 신경망에 있는 모든 layer에 대해서 학습을 수행하는 것이 아니라, (b)와 같이 신경망에 있는 입력층이나 은닉층의 일부 뉴런을 생략(dropout)하고, '줄어든 신경망'을 통해 학습을 수행한다.
일정한 mini-batch 구간 동안 생략된 망에 대한 학습이 끝나면, 다시 무작위로 다른 뉴런들을 생략하면서 반복적으로 학습을 수행한다.
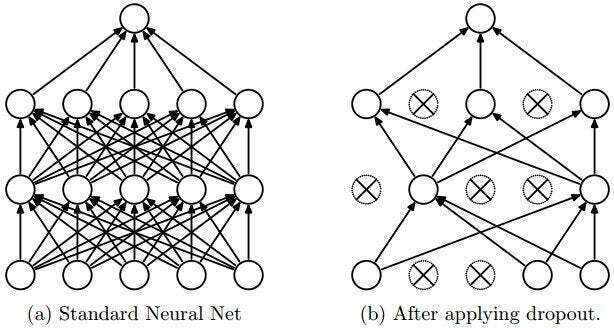
매 훈련 스텝에서 각 뉴런(입력 뉴런은 포함, 출력 뉴런은 제외)은 임시적으로 드롭아웃될 확률 를 가진다. 하이퍼파라미터 를 드롭아웃 비율이라고 하고 보통 10%와 50% 사이를 지정한다.
드롭아웃으로 훈련된 뉴런은 이웃한 뉴런에 맞춰 적응될 수 없으므로 가능한 한 자기 자신이 유용해져야 한다. 또 이런 뉴런들은 몇 개의 입력 뉴런에만 지나치게 의존할 수 없다. 모든 입력 뉴런에 주의를 기울여야 하기 때문에 입력값의 작은 변화에 덜 민감해진다. 결국 더 안정적인 네트워크가 되어 일반화 성능이 좋아진다고 할 수 있다.
✅ max-norm 규제
맥스-노름 규제는 각각의 뉴런에 대해 입력의 연결 가중치 가 이 되도록 제한한다(은 맥스-노름 하이퍼파라미터).
맥스-노름 규제는 전체 손실 함수에 규제 손실 항을 추가하지 않는다. 대신 일반적으로 매 훈련 스텝이 끝나고 를 계산하고 필요하면 의 스케일을 조정한다(). 을 줄이면 규제의 양이 증가하여 과대적합을 감소시키는 데 도움이 된다. 맥스-노름 규제는 (배치 정규화를 사용하지 않았을 때) 불안정한 그레이디언트 문제를 완화하는 데 도움을 줄 수 있다.
