Intro
논문 작성을 위해 LP (Linear Programming) Solver를 구현해야 할 일이 있었다. LP 자체는 옛날부터 이어져온 오래된 문제다보니 코드는 많을거라 생각했는데, Google이 제공하는 OR-Tools에서도 LP solver 라이브러리를 제공하여 이를 사용했다. 내가 이해한 바로는 변수나 constraint 등을 동적으로 주는 방법은 찾지 못하여 constraint 식과 objective 식을 주면 해를 찾도록 하는 모듈을 간단하게 구현하였다. 이미 구현된 많은 tool이 있겠지만 python으로 간단하게 LP Solver를 사용하고 싶을 때 이 글을 참고해도 좋을 것 같다.
Usage
public repo로 만들어서 clone 후 사용 가능하다.
[Requirement]
- Python 3.6 이상 version
- PIP (정확히 몇 version부터인지는 모르겠으나 옛날 version에서는 안 깔린다.)
python -m pip install --upgrade pip
python -m pip install ortools argparse[실행]
git clone https://github.com/Spiraline/LP_solver.git
cd LP_solver
python lp_solver.py -i $(input 파일 경로)[parameter]
- input (
-i): input 파일 경로 - delimiter (
-d): input 파일의 delimiter. 기본값은 공백이다. - verbose (
-v): OR-Tools가 제공하는 log message를 킬 것인지에 대한 flag다.
[input 파일 형식]
- Line 1: (변수의 개수) (constraint 식의 개수)
- Line 2: (min/max) objective 함수의 계수
- Line 3~: constraint 식의 계수 (부등호 혹은 등호는
ge,le,eq로 표기)
아래의 예시를 보면 이해가 더 빠르다.
Example
아래 LP Problem을 푼다고 하자. (Google OR-Tools에서도 제공하는 예시다.)
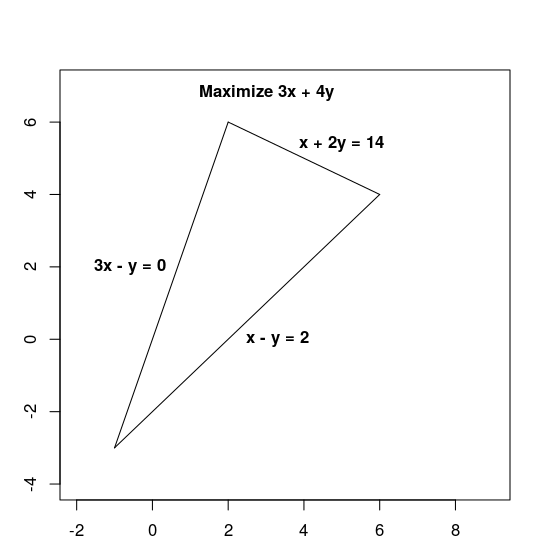
내 모듈의 input으로 변환하면 아래와 같다. (repo의 example 파일로 추가해놓았다.)
2 3
max 3 4
1 -1 le 2
3 -1 ge 0
1 2 le 14python lp_solver.py -i example로 실행 시
[5.999999999999998, 3.9999999999999996] 33.99999999999999이 출력된다. x=6, y=4일때 34로 최대값이라는 의미이다.
해가 없는 경우 해가 없다고 메시지가 출력된다.
간단한 코드 구조
내 코드를 설명하기보다 Google OR-Tools에서 제공하는 예시를 설명하는 것이 더 쉬워보여서 가져왔다.
from ortools.linear_solver import pywraplp
def LinearProgrammingExample():
solver = pywraplp.Solver.CreateSolver('GLOP')
x = solver.NumVar(0, solver.infinity(), 'x')
y = solver.NumVar(0, solver.infinity(), 'y')
# Constraint 0: x + 2y <= 14.
solver.Add(x + 2 * y <= 14.0)
# Constraint 1: 3x - y >= 0.
solver.Add(3 * x - y >= 0.0)
# Constraint 2: x - y <= 2.
solver.Add(x - y <= 2.0)
# Objective function: 3x + 4y.
solver.Maximize(3 * x + 4 * y)
# Solve the system.
status = solver.Solve()
Solver를 만들고 NumVar로 변수를 추가한 후, Add로 constraint를 추가하고, Maximize로 objective 함수를 선언할 수 있다.
이 과정을 동적으로 할 수 있게 수정했다.
