Regression Filter (C++)

사담

만든지 오래된 Tool이기도 하고 (작년 5월에 만들었다) 간단해서 올릴까 고민했으나, 블로그에 거창한 것만 올리면 글 리젠이 너무 길어질 듯한 생각이 들어 올리기로 했다. Tool을 만들게 된 계기는 속도 data를 smoothing해야 할 일이 있어 Kalman Filter를 구현해보려다가 원리는 알겠는데 식이 찾아보는 곳마다 달라서 그냥 선형회귀로 간단하게 Filter를 구현하기로 했다. 개인적으로 Tool은 코딩하기 쉬운 Python으로 만들고 있었으나 Autoware 코드들이 C++로 구현되어 있어 연동을 위해 오랜만에 C++로 구현했다. 안타까운 건 outlier data가 생기는 것이 issue였어서 regression filter 없이 min-max filter만 적용해도 문제가 해결되었다.. 😥

사용법

public repo에 있기 때문에 clone 후 바로 사용 가능하다.

git clone https://github.com/Spiraline/serial-data-smoothing.git
cd serial-data-smoothing
g++ regression_filter.cpp -o smoothing
./smoothing $(input_file_path) $(output_file_path) $(history_size)

간단한 Tool이라 parameter가 적다. input file path에 들어갈 파일은 new line으로 구분된 숫자들이 있는 텍스트 파일이어야 하며, output file의 형식도 마찬가지다.
history size의 경우 회귀식을 만들기 위해 사용할 이전 data의 수를 의미한다. 아래에서 더 자세히 설명하겠다.

선형 회귀 분석

선형 분석도 다양한 종류가 있다. 우리가 어떤 함수 $Y=f(X)$를 생각할 때 영향을 주는 변수에 해당하는 $X$ (하나가 아닐 수 있다)를 독립 변수로, 영향을 받는 변수 $Y$를 종속 변수라고 한다. 종속 변수나 독립 변수의 수에 따라 회귀 모델을 아래와 같이 분류한다고 한다.

• 종속 변수 1개 : 단변량 선형 회귀 모델

• 종속 변수 2개 이상 : 다변량 선형 회귀 모델

• 독립 변수 1개 : 단순 선형 회귀 모델

• 독립 변수 2개 이상 : 다중 선형 회귀 모델

일반적으로는 단변량 다중 선형 회귀 모델을 많이 사용한다고 하나, 나의 경우에는 독립 변수가 1개였기 때문에 단변량 단순 선형 회귀 모델을 사용했다. 다중 선형 회귀 모델이더라도 단순히 이 경우를 확장한 것이라 한다.

단변량 단순 선형 회귀 모델

상당히 단순하다. 사실 $\alpha$, $\beta$를 어떤 값으로 잡더라도 그 식으로 근사했다고 하면 아무튼 선형 회귀이지만, 우리는 더 좋은 회귀식을 원한다. 그렇다면 더 좋은 회귀식은 무엇일까? 직관적으로는 모든 점들과 가장 가까운 선일 것이고, 위 수식과 연관짓자면 오차항인 e를 최소로 만드는 식을 의미한다.

SSE (Sum of Squared Errors)를 최소화하는 $\alpha$, $\beta$를 위처럼 최소제곱법으로 계산하면 아래와 같다.

본 코드도 위 식을 바탕으로 작성되었다. 또한 history size는 위 식에서의 i에 해당하여 이전 i개의 data를 기준으로 회귀식을 만든다고 생각하면 된다.
여담으로 이차식으로 회귀하는 식도 생각보다 간단하여 구현은 했으나 성능이 선형 회귀식과 같아서 Autoware에 적용할 때는 선형 회귀식으로 만든 filter를 적용했다.

Example

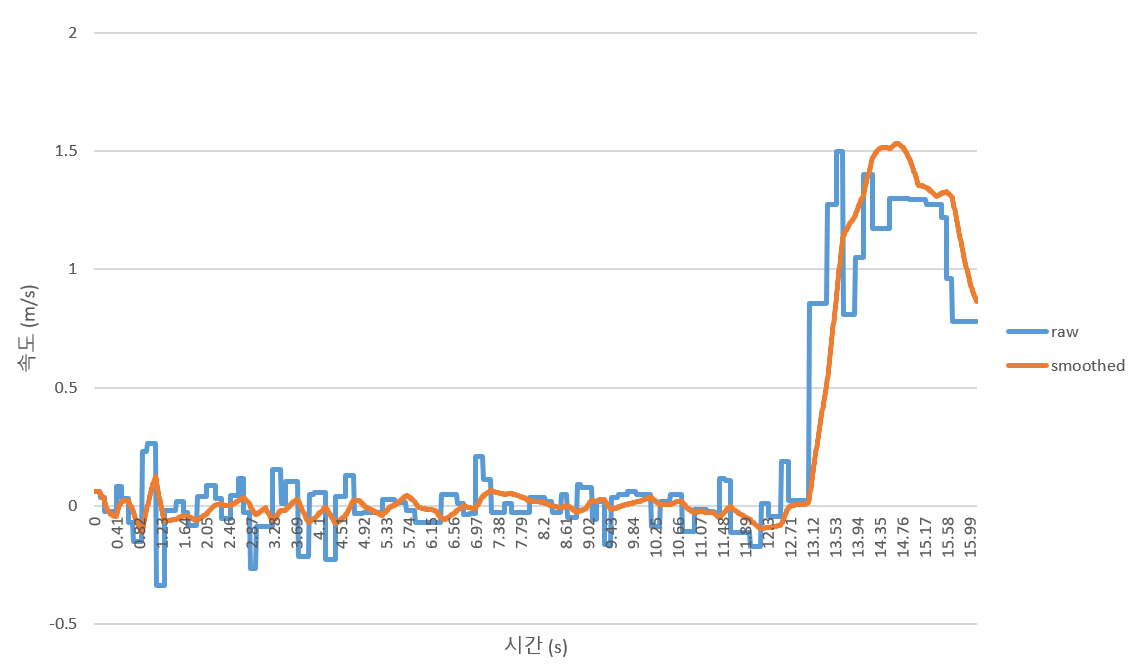
input, output data를 excel을 이용해서 그래프로 그린 결과다. 속도가 100Hz로 출력된 값을 사용하여 history size를 200으로 설정하고 smoothing했다. 회귀식의 특성 상 주식 차트에서의 이동평균선의 모습처럼 보이는데, 이평선의 특징처럼 history size가 커지면 smoothing은 더 잘 되나, 반대로 현재 값의 반영이 잘 안 된다는 trade-off가 생긴다. 모든 filter가 smoothing 성능과 반응성 사이의 trade-off를 가지고 있다고 한다.