최근에는 TSP 같은 최적화 문제를 신경망으로 개발하는 것이 학문적 관심사이다. 이 글은 최근에 제시된 모델 아키텍처와 러닝 패러다임을 하나의 프레임워크로 통합하는 신경망 조합 최적화 파이프라인을 제시한다. 파이프라인의 렌즈를 통해 경로 문제를 위한 딥러닝 발전을 분석하고 실용적이기 위한 미래 연구 방향을 제공한다.
This article is joint work with Rishabh Anand, a rising undergraduate at the National University of Singapore (NUS) studying Computer Science and Pure Mathematics. The article was also accepted at the inaugural ICLR 2022 Blog Track!
Table of Contents
- 조합 최적화 문제의 배경
- TSP and Routing Problems
- 경로 문제를 푸는 딥러닝
- 뉴럴 조합 최적화
- 통합 뉴럴 조합 최적화 파이프라인
(1) 그래프로 문제 정의
(2) 그래프 노드와 엣지에 대한 잠재 임베딩 구하기
(3,4) 임베딩을 솔루션으로 변환하기
(5) 모델 훈련하기 - 파이프라인을 통해 탁월한 논문들의 특징을 분류
- 최근의 진보와 애브뉴
- Equivariance and Symmetries를 활용하기
- 그래프 탐색 알고리즘의 개선
- 부분적으로 최적인 솔루션을 개선하는 러닝
- Learning Paradigms that Promote Generalization
- 평가 프로토콜 개선
- Summary

1. 조합 최적화 문제의 배경
조합 최적화는 수학과 컴퓨터 사이언스와 교차하는 실용적인 분야로서 NP-Hard인 한정된 최적화 문제를 푸는 것이 목표이다. NP-Hard 문제는 모든 솔루션을 탐색하기에는 너무 복잡하다.
이것에 관심이 있는 이유는? 유명한 문제에 대한 탄탄하고 신뢰있는 근사 알고리즘은 수많은 실제적인 응용들이 있으며 현대 산업의 근간이기 때문이다. 예를 들어 TSP가 가장 유명한 조합최적화 문제이며 물류 최적화와 스케줄링부터 유전자 분석과 시스템 생물학과 같이 다양하다.
TSP와 경로 문제
TSP is also a classic example of a Routing Problem – Routing Problems are a class of COPs that require a sequence of nodes (e.g. cities) or edges (e.g. roads between cities) to be traversed in a specific order while fulfilling a set of constraints or optimising a set of variables. TSP requires a set of edges to be traversed in an order that ensures all nodes are visited exactly once. In the algorithmic sense, the optimal “tour” for our salesperson is a sequence of selected edges that provides the minimal distance or time taken over a Hamiltonian cycle, see Figure 1 for an illustration.
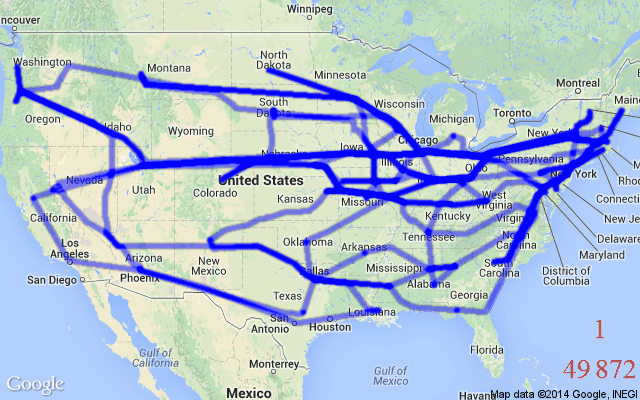
Figure 1: TSP asks the following question:(Source: MathGifs)
도시들과 모든 도시들간의 거리가 주어지면 영업사원이 모든 도시를 방문하고 원 위치하는데 가장 짧은 경로는 무엇일까?
실제의 경로 문제 또는 VRP는 단순한 TSP를 뛰어넘는 어려운 제약사항을 다룬다. 타임윈도우 TSP는 TSP 그래프에 타임윈도우 제약이 있는 노드를 다룬다. 타임윈도우란 어떤 노드들은 고정된 시간 사이에만 방문이 가능하다. CVRP의 경우는 여러대의 차량으로 여러 도시를 방문하며 각 차량은 최대 적재량이 다르다.
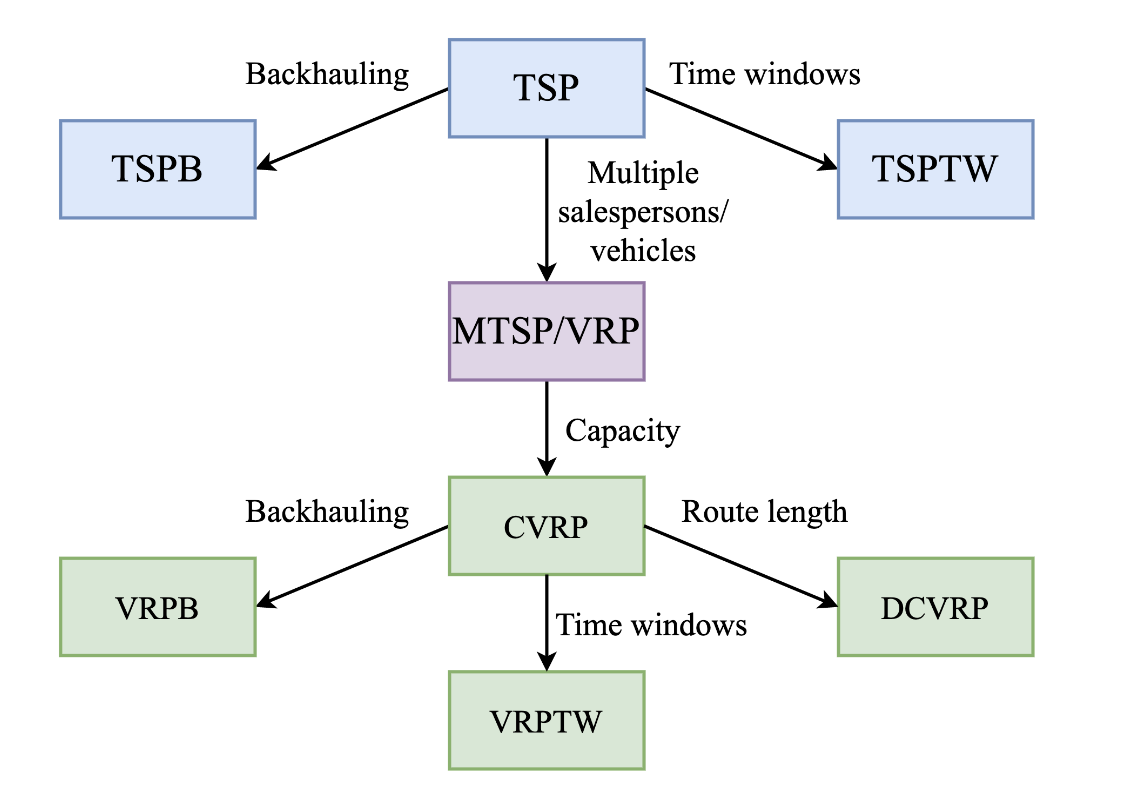
Figure 2: TSP와 VRP와 연관된 클래스. VRP들은 제약사항에 의해 분류되며 이 그림은 비교적 잘 연구된 것들을 보여준다. There could be VRPs in the wild with more complex and non-standard constraints! (Source: adapted from Benslimane and Benadada, 2014)
경로 문제를 푸는 딥러닝
경로 문제를 위한 신뢰있는 알고리즘과 해결사를 개발하려면 상당한 전문가적 직관과 수년간의 실험이 필요하다. 예를 들어 최신의 TSP 해결사인 Concorde는 선형 프로그래밍, 커팅 평면 알고리즘과 브랜치-바운드에 관해 50년간의 연구가 뒷받침되었다.
Concorde는 수십개에서 수천개의 노드들에 대한 최적 솔루션을 찾을 수 있으나 실행 시간이 매우 길다. 실제로 용량 제한이나 타임 윈도우 같은 제약을 다루려면 어렵기도 하지만 시간이 많이 걸린다.
이것이 머신러닝 커뮤니티가 다음 질문을 받게된 이유이다.
Can we use deep learning to automate and augment expert intuition required for solving COPs?
See this masterful survey from Mila for more in-depth motivation: Bengio et al., 2020.
신경망 조합 최적화
신경망 조합 최적화는 COP 문제를 해결하기 위한 망치로 딥러닝을 사용하려고 하는 것이다. 신경망은 문제 자체로부터 직접 학습하여 COP에 대한 근사적 솔루션을 만들어 내도록 훈련된다.
이 연구는 구글브레인에서 Seq2seq Pointer 네트워크와 Neural Combinatorial Optimization with RL 논문에서 시작되었다.
요즘에는 Graph Neural Networks가 딥러닝 기반 해결사의 핵심의 아키택처이며 이러한 문제들의 그래프 구조를 다룬다.
이 방식은 다음과 같은 방식으로 기존의 COP 해결사 보다 뛰어나다
-
수작업인 휴리스틱이 없음 전문가가 수작업으로 휴리스틱과 규착을 설계하는 대신 신경망이 최적 해결사를 모방하거나 강화 학습으로 그들을 학습한다.
-
GPUs 상에서 빠른 추론. 기존의 해결사는 규모가 큰 문제를 막대한 시간이 걸린다. 신경망이 COP 해결사로 훈련되면 적정한 시간 복잡도를 가지며 GPU로 병렬화가 가능하다. 이 때문에 실시간 의사결정이나 경로 문제에 매우 바람직하다.
-
난해한 제약이 있거나 연구 중인 COP를 다룸. 난해한 제약이 있는 새롭거나 덜 연구된 문제에 대한 문제 별 해결사의 개발은 신경 조합 최적화를 통해 크게 가속화될 수 있습니다. 이러한 문제는 종종 과학적 발견이나 컴퓨터 아키텍처에서 나타난다. 예를 들어 구글의 TPU 칩 설계 시스템이 있습니다. 차세대 신경망을 위한 TPU가 신경망애 의해 설계된다.
2. COP 파이프라인
전형적인 예제로 TSP를 사용하여 이제 여러 라우팅 문제에 대한 최신 딥 러닝 기반 접근 방식을 특성화하는 데 사용할 수 있는 일반적인 신경망 COP 파이프라인을 제시한다.
TSP에 대한 최첨단 방식은 도시의 위치 좌표를 입력으로 사용하고 GNN 또는 트랜스포머를 고전적인 그래프 검색 알고리즘과 결합하여 근사 솔루션을 구축한다.
아키텍처는 크게 다음과 같이 분류할 수 있다.
(1) 단계별 방식으로 솔루션을 구축하는 오토리그레션 방식
(2) 한 번에 솔루션을 생성하는 비 오토리그레션 모델. 지도 학습 또는 강화 학습을 통해 TSP 방문 거리를 최소화하여 최적의 해결사를 모방하도록 모델을 훈련할 수 있다.

Figure 3: 신경망 CO 파이프라인(Source: Joshi et al., 2021).
Joshi et al., 2021에서 가져온 이 파이프라인은 탁월한 모델 아키텍처와 러닝 패러다임을 통합된 프레임워크로 묶어준다. 이를 통해 라우팅 문제에 대한 딥 러닝의 최근 개발을 분석 및 분석하고 향후 연구를 자극할 새로운 방향을 제시할 수 있다.
(1) 그래프로 문제 정의
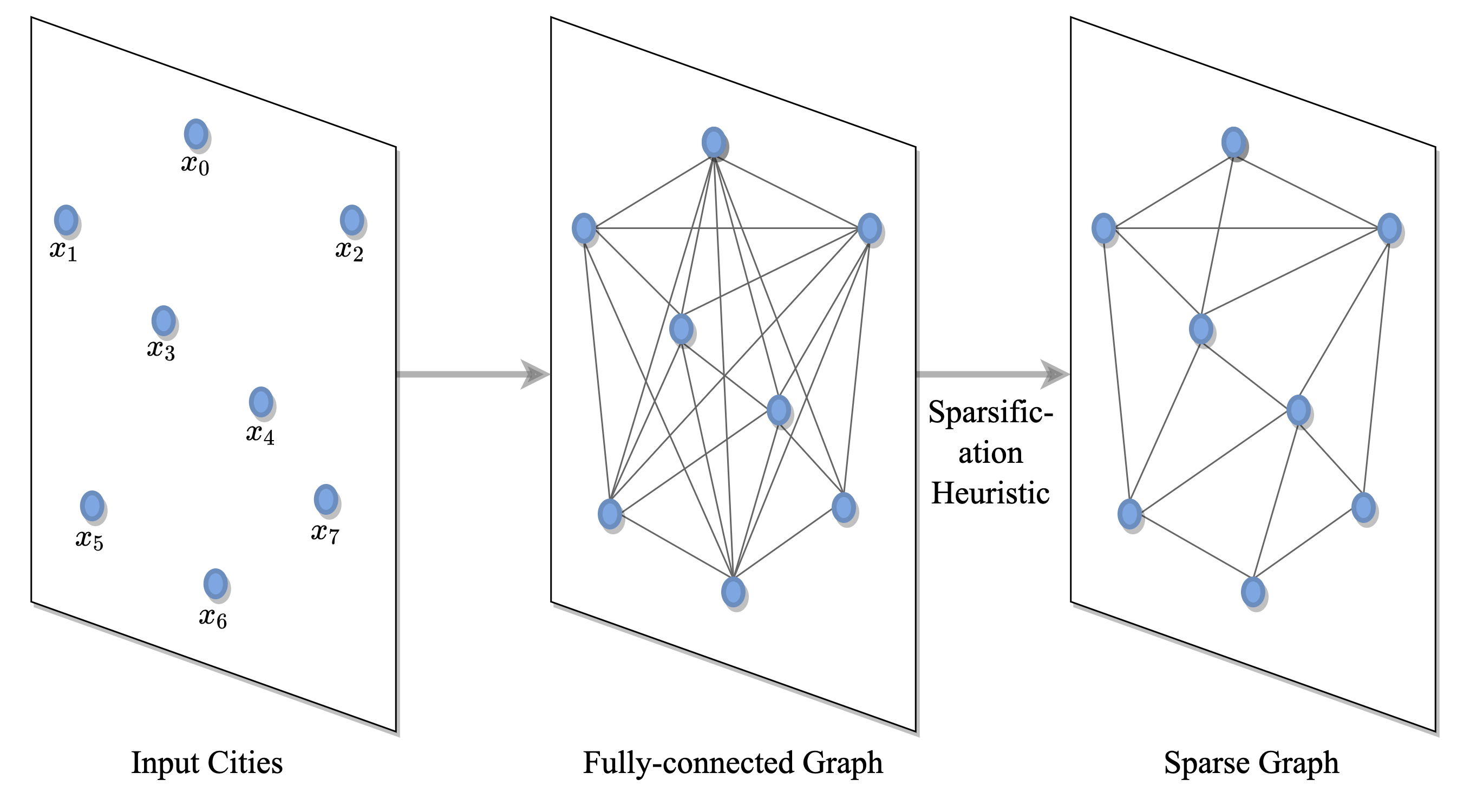
Figure 4: 문제 정의: TSP는 도시/노드 연결 그래프로 구성.
TSP는 노드가 도시에 해당하고 엣지가 이들 사이의 도로를 나타내는 완전 연결된 그래프를 통해 표현된다. 그래프는 k-최근접 이웃과 같은 휴리스틱을 통해 희소화될 수 있다. 이를 통해 모델은 모든 노드에 대한 쌍별 계산이 다루기 힘든 대규모 인스턴스로 확장되거나[Khalil et al., 2017] 검색 공간을 줄여 더 빠르게 학습할 수 있다[Joshi et al., 2019].
(2) 그래프 노드와 엣지에 대한 잠재적 임베딩 구하기
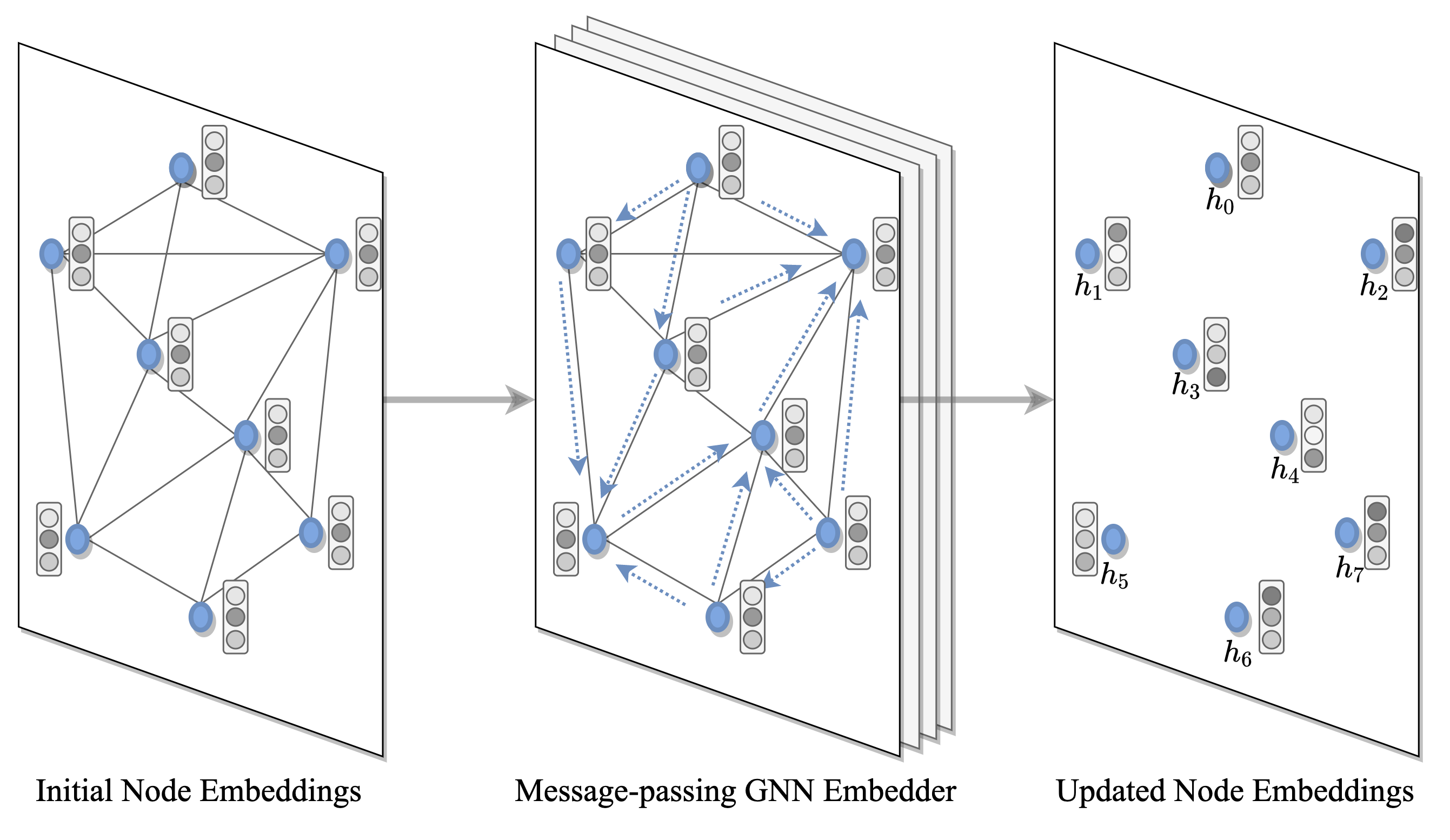
Figure 5: 그래프 임베딩: 각 그래프 노드에 대한 임베딩은 GNN 인코더를 사용하여 구한다. 이것은 재귀적으로 각 노드의 이웃으로부터 피처들을 수집하여 지역적인 구조적 특징을 구축한다.
GNN 또는 트랜스포머 인코더는 입력에 있는 각 노드와 엣지에 대한 은닉된 표현 또는 임베딩을 인코딩한다. 각 레이어에서 노드들은 재귀적 메시지 패싱을 통해 이웃으로부터 피처들을 모아 지역적 구조를 표현한다. L개의 레이어들이 쌓이면 신경망이 각 노드의 L만큼 떨어진 이웃으로부터 표현을 구축하도록 해준다.
트랜스포머와 같은 Anisotropic and 어텐션 기반 GNN과 Gated Graph ConvNets[Joshi et al., 2019]을 인코딩 경로 문제에 많이 사용한다. 이웃을 수집하는 동안 각 노드가 당면한 작업을 해결하기 위한 상대적 중요성에 따라 이웃을 평가할 수 있도록 하기 때문에 어텐션 메카니즘이 중요하다.
Importantly, the Transformer encoder can be seen as an attentional GNN, i.e. Graph Attention Network (GAT), on a fully-connected graph. See this blogpost for an intuitive explanation.
(3 + 4) 임베딩을 개별 솔루션으로 변환하기
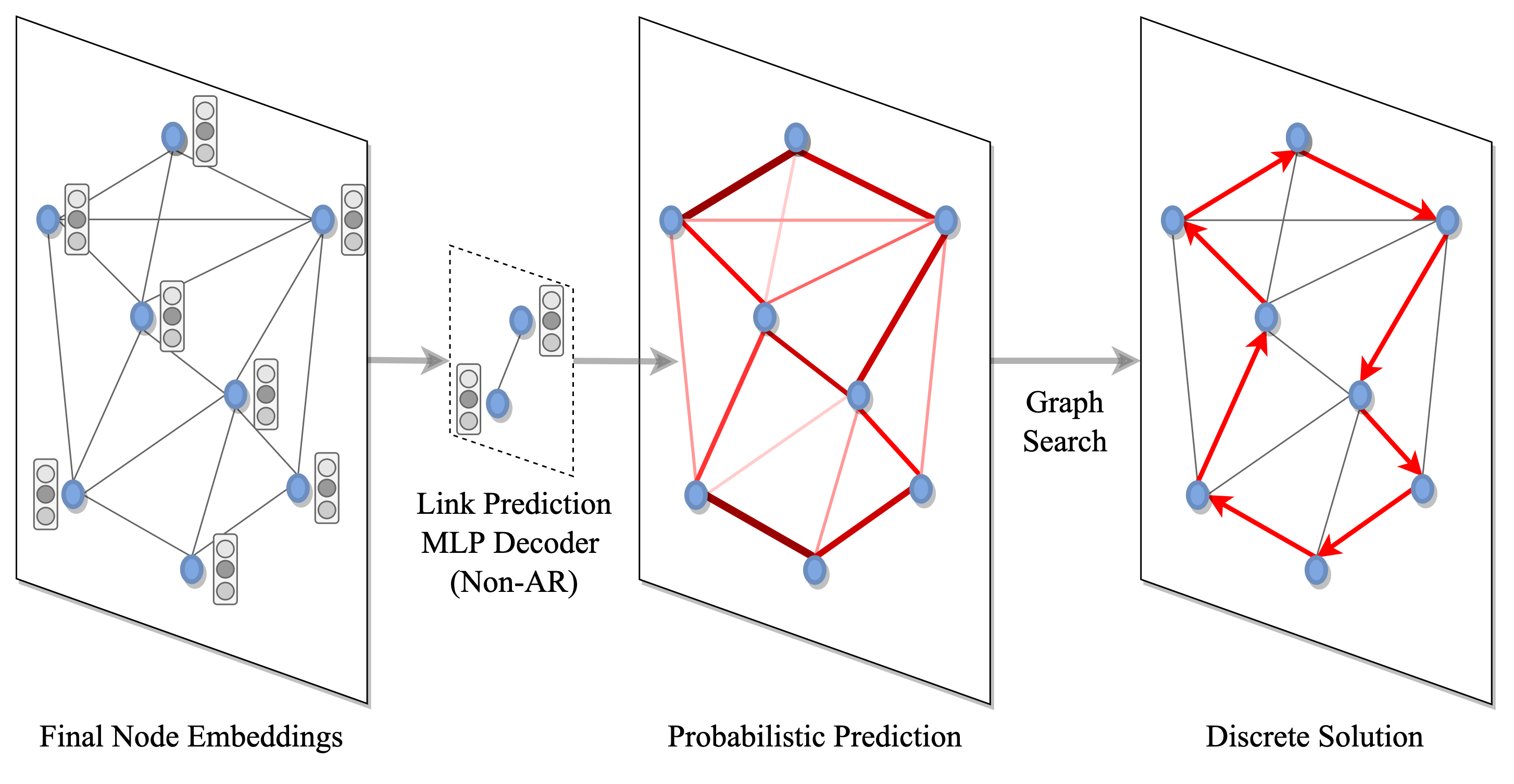
Figure 5: 솔루션 디코딩과 탐색: 솔루션 집합에 속하는 각 노드 또는 에지에 확률이 할당되고(여기서 MLP는 에지 확률의 '히트맵'을 얻기 위해 에지별로 예측을 수행함) 탐욕적 탐색 또는 빔 탐색과 같은 그래프 탐색 기술을 통해 개별적 결정으로 변환됩니다.
일단 그래프의 노드와 엣지가 잠재적 표현으로 인코딩되면 개별적인 TSP 솔루션으로 디코딩되어야 한다. 이것은 두 단계로 이루어 진다.
먼저, 서로간에 독립적이거나 그래프 순회를 통해 조건적으로 (즉 자동회귀 디코딩) 솔루션 집합에 속하는 각 노드와 엣지에 확률을 지정한다.
다음에, 예측 확률은 고전적인 그래프 탐색 기법을 통해 이산적 결정으로 변환된다.
디코더의 선택에는 데이터 효율성과 구현 효율성 사이의 균형이 따릅니다. 자동회귀 디코더[Kool et al., 2019]는 TSP를 Seq2Seq 또는 언어 번역 작업으로 정렬되지 않은 도시 집합에서 정렬된 투어로 캐스팅합니다. 한 번에 하나의 노드를 단계별로 선택하여 라우팅 문제의 순차적 귀납 편향을 명시적으로 모델링합니다. 반면에 비자동회귀 디코더[Joshi et al., 2019]는 TSP를 에지 확률 히트맵을 생성하는 작업으로 캐스팅합니다. NAR 접근 방식은 단계별이 아닌 한 번에 예측을 생성하므로 훨씬 빠르고 실시간 추론에 더 적합합니다. 그러나 TSP의 순차적 특성을 무시하고 AR 디코딩과 비교했을 때 훈련 효율이 떨어질 수 있습니다[Joshi et al., 2021].
(5) 모델의 훈련
마지막으로, 전체 인코더-디코더 모델은 비전 또는 자연어 처리와 같은 딥러닝 모델처럼 훈련된다. 가장 단순한 경우 최적 해결사의 모방을 통해(지도 학습) 최적 솔루션에 근접한 솔루션을 만들도록 훈련시킨다. TSP의 경우 Concrode 해결사를 훈련 집합을 만들어내는데 사용한다. AR 디코더가 있는 모델은 teacher-forcing을 통해 훈련하여 투어 노드의 최적 순서[Vinyals et al., 2015]를 출력하도록 한다.
강화학습은 아직 연구중인 문제와 같이 정답이 없는 경우에는 탁월한 대안이다. 경로 문제는 일반적으로 비용 함수(예상시간과 같이)룰 최소화하기 위한 순차적 의사결정아 필요하다. 이는 보상을 최대화하는 에이전트를 훈련하는 강화학습 프레임워크로 만들 수 있다. AR 디코더를 가진 모델은 표준 정책 그라디언트 알고리즘[Kool et al., 2019] 또는 Q러닝[Khalil et al., 2017]으로 훈련할 수 있다.
3. 파이프라인을 통해 뛰어난 논문들의 분류
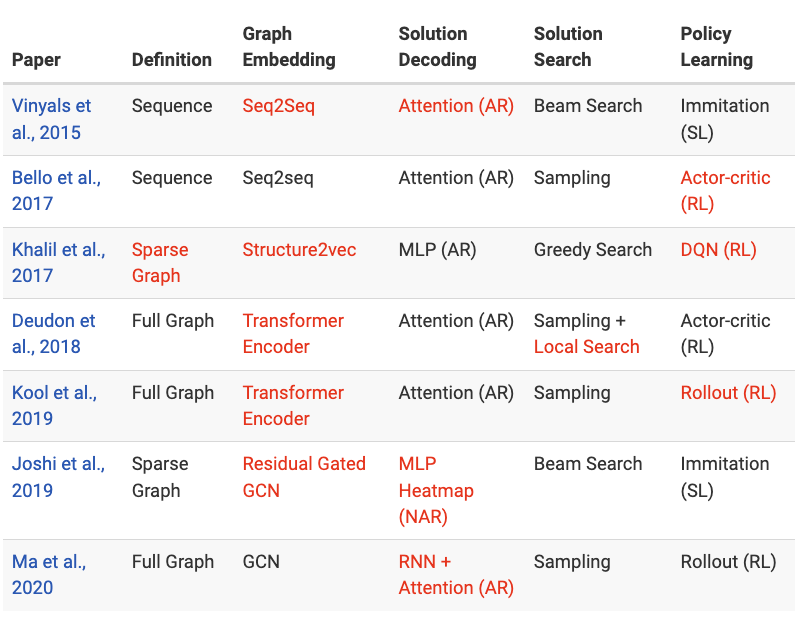
5단계 파이프라인을 통해 TSP를 위한 딥러닝에서 두드러진 작업을 특성화할 수 있다. 파이프라인은 (1) 문제 정의 → (2) 그래프 임베딩 → (3) 솔루션 디코딩 → (4) 솔루션 탐색 → (5) 정책 학습으로 구성된다.
4. 향후 작업을 위한 최근의 발전 및 방법
라우팅 문제에 대한 딥러닝의 최근의 진화와 트렌드를 5단계 파이프라인으로 알아보았다. 그리고 대규모와 실제 현장의 케이스의 일반화를 개선하는데 초점을 둔 몇가지 미래의 연구 방향을 보여준다.
등가와 대칭을 활용하기
가장 영향력 있는 초기 작업 중 하나인 자동재귀적 어텐션 모델[Kool et al., 2019]은 TSP를 Seq2Seq 언어 번역 문제로 간주하고 TSP 투어를 도시의 순열로 순차적으로 구성한다. 이 공식의 한 가지 즉각적인 단점은 라우팅 문제의 기본 대칭을 고려하지 않는다는 것이다.
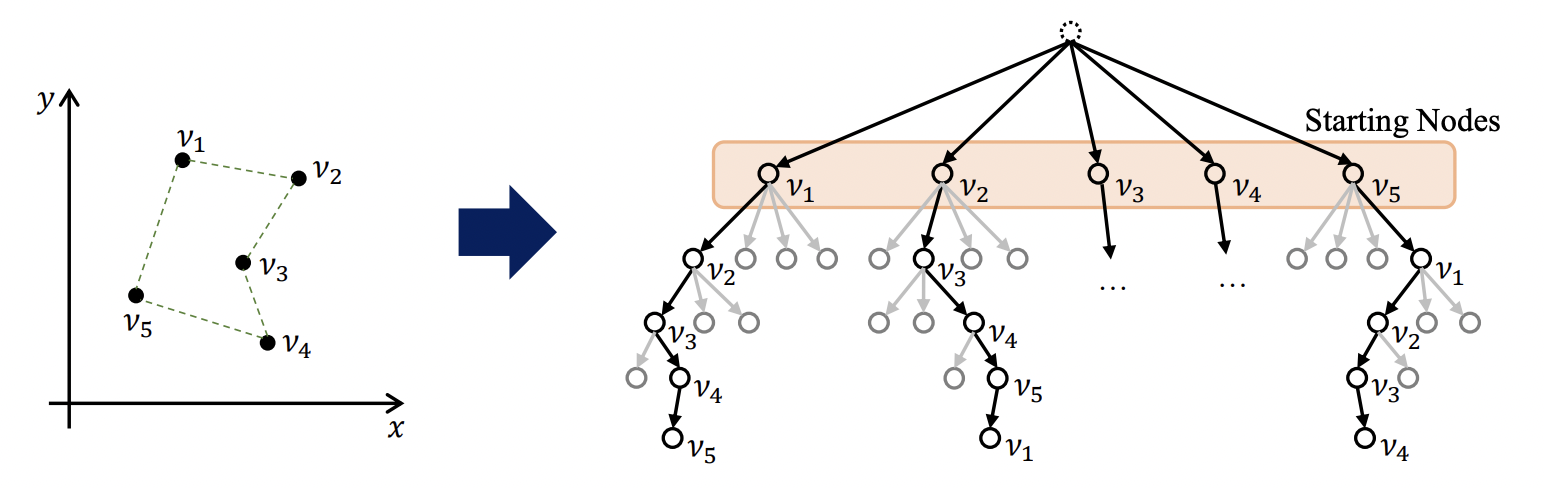
Figure 6: In general, a TSP has one unique optimal solution (L). However, under the autoregressive formulation when a solution is represented as a sequence of nodes, multiple optimal permutations exist (R). (Source: Kwon et al., 2020)
POMO: Policy Optimization with Multiple Optima [Kwon et al., 2020] proposes to leverage invariance to the starting city in the constructive autoregressive formulation. 동일한 어텐션 모델을 훈련하지만 다중의 최적 투어 조합의 존재를 탐색하는 새로운 강화학습을 사용한다(step 5)
Techtonic 2020 - POMO: 강화학습을 이용한 조합최적화 - 권영대 프로
Techtonic 2021 - AI를 사용해 기업의 조합최적화 작업을 처리할 수 있을까? (NeurIPS 2021) - 권영대 프로
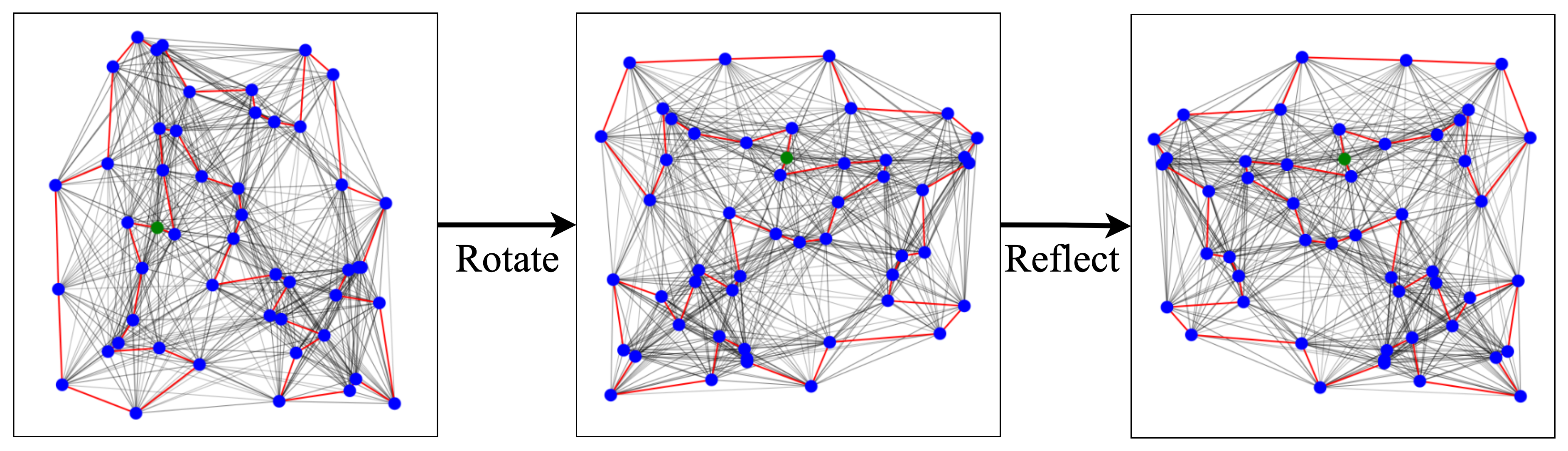
Figure 7: TSP solutions remain unchanged under the Euclidean symmtery group of rotations, reflections, and translations to the city coordinates. Incorporating these symetries into the model may be a principled approach to tackling large-scale TSPs.
Similarly, a very recent ugrade of the Attention model by Ouyang et al., 2021 considers invariance with respect to rotations, reflections, and translations (i.e. the Euclidean symmetry group) of the input city coordinates. They propose an autoregressive approach while ensuring invariance by performing data augmentation during the problem definition stage (pipeline step 1) and using relative coordinates during graph encoding (pipeline step 2). Their approach shows particularly strong results on zero-shot generalization from random instances to the real-world TSPLib benchmark suite.
Future work may follow the Geometric Deep Learning (GDL) blueprint for architecture design. GDL tells us to explicitly think about and incorporate the symmetries and inductive biases that govern the data or problem at hand. As routing problems are embedded in euclidean coordinates and the routes are cyclical, incorporating these contraints directly into the model architectures or learning paradigms may be a principled approach to improving generalization to large-scale instances greater than those seen during training.
개선된 그래프 탐색 알고리즘
Another influential research direction has been the one-shot non-autoregressive Graph ConvNet approach [Joshi et al., 2019]. Several recent papers have proposed to retain the same Gated GCN encoder (pipeline step 2) while replacing the beam search component (pipeline step 4) with more powerful and flexible graph search algorithms, e.g. Dynamic Programming [Kool et al., 2021] or Monte-Carlo Tree Search (MCTS) [Fu et al., 2020].
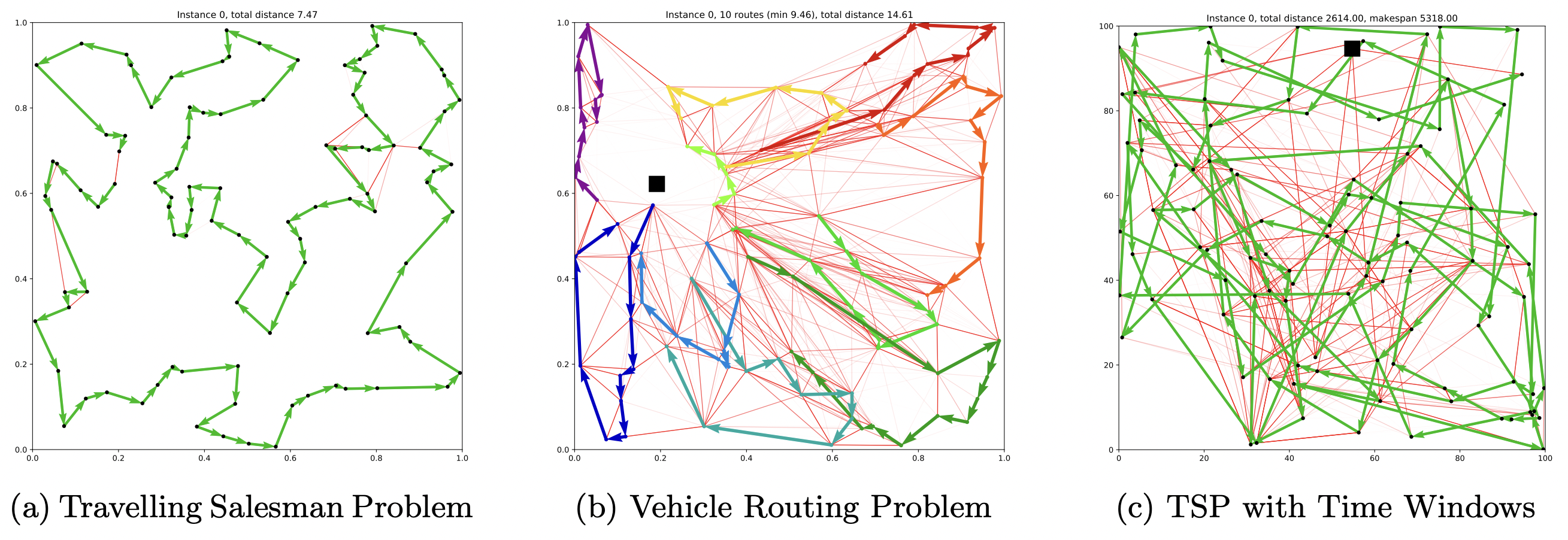
Figure 8: The Gated GCN encoder [Joshi et al., 2019] can be used to produce edge prediction 'heatmaps' (in transparent red color) for TSP, CVRP, and TSPTW. These can be further processed by DP or MCTS to output routes (in solid colors). The GCN essentially reduces the solution search space for sophisticated search algorithms which may have been intractable when searching over all possible routes. (Source: Kool et al., 2021)
The GCN + MCTS framework by Fu et al. in particular has a very interesting approach to training models efficiently on trivially small TSP and successfully transferring the learnt policy to larger graphs in a zero-shot fashion (something that the original GCN + Beam Search by Joshi et al. struggled with). They ensure that the predictions of the GCN encoder generalize from small to large TSP by updating the problem definition (pipeline step 1): large problem instances are represented as many smaller sub-graphs which are of the same size as the training graphs for the GCN, and then merge the GCN edge predictions before performing MCTS.
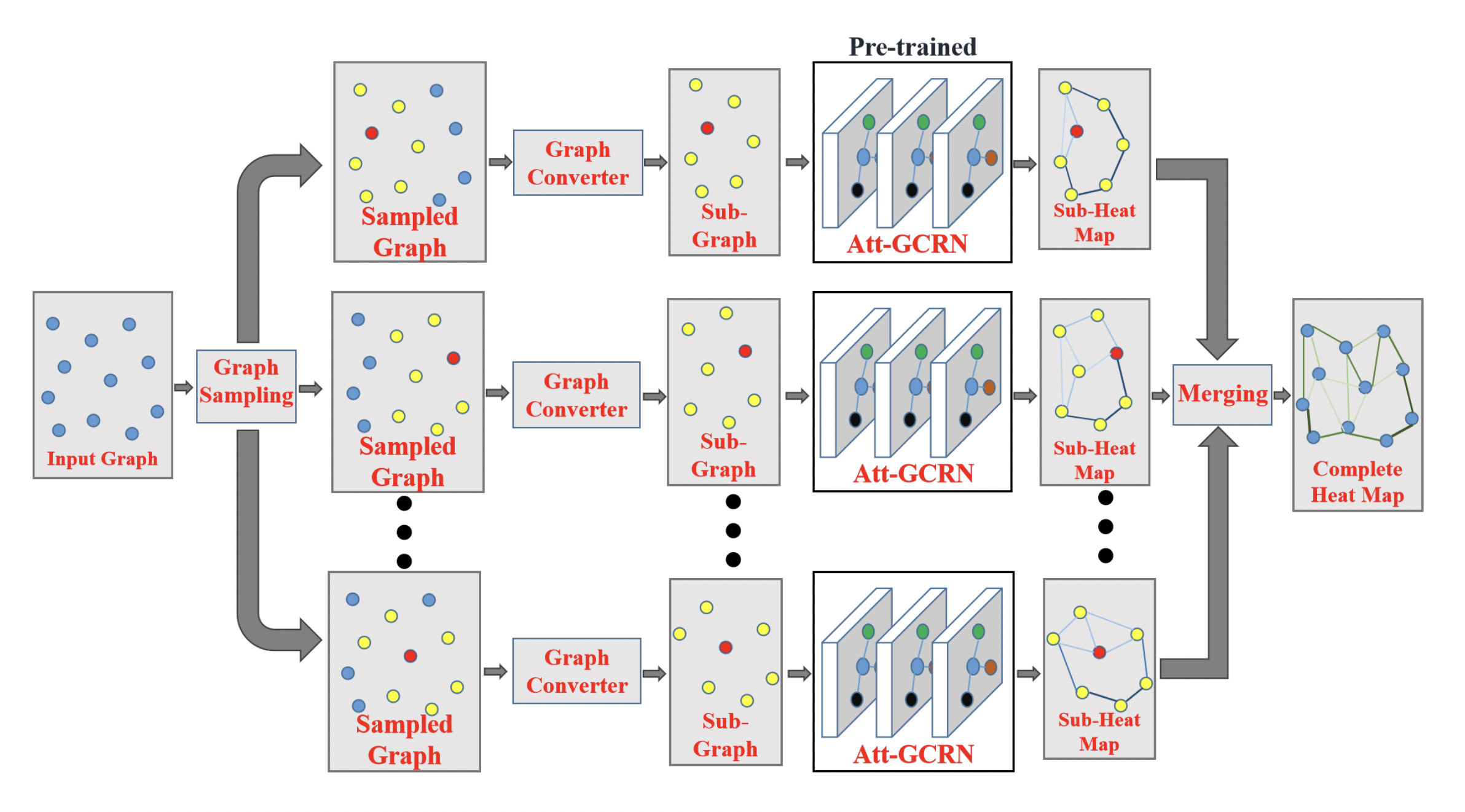
Figure 9: The GCN + MCTS framework [Fu et al., 2020] represents large TSPs as a set of small sub-graphs which are of the same size as the graphs used for training the GCN. Sub-graph edge heatmaps predicted by the GCN are merged together to obtain the heatmap for the full graph. This divide-and-conquer approach ensures that the embeddings and predictions made by the GCN generalize well from smaller to larger instances. (Source: Fu et al., 2020)
Originally proposed by Nowak et al., 2018, this divide-and-conquer strategy ensures that the embeddings and predictions made by GNNs generalize well from smaller to larger TSP instances up to 10,000 nodes. Fusing GNNs, divide-and-conquer, and search strategies has similarly shown promising results for tackling large-scale CVPRs up to 3000 nodes [Li et al., 2021].
Overall, this line of work suggests that stronger coupling between the design of both the neural and symbolic/search components of models is essential for out-of-distribution generalization [Lamb et al., 2020]. However, it is also worth noting that designing highly customized and parallelized implementations of graph search on GPUs may be challenging for each new problem.
부분적 최적화 솔루션을 학습하기
Recently, a number of papers have explored an alternative to constructive AR and NAR decoding schemes which involves learning to iteratively improve (sub-optimal) solutions or learning to perform local search, starting with Chen et al., 2019 and Wu et al., 2021. Other notable papers include the works of Cappart et al., 2021, da Costa et al., 2020, Ma et al., 2021, Xin et al., 2021, and Hudson et al., 2021.
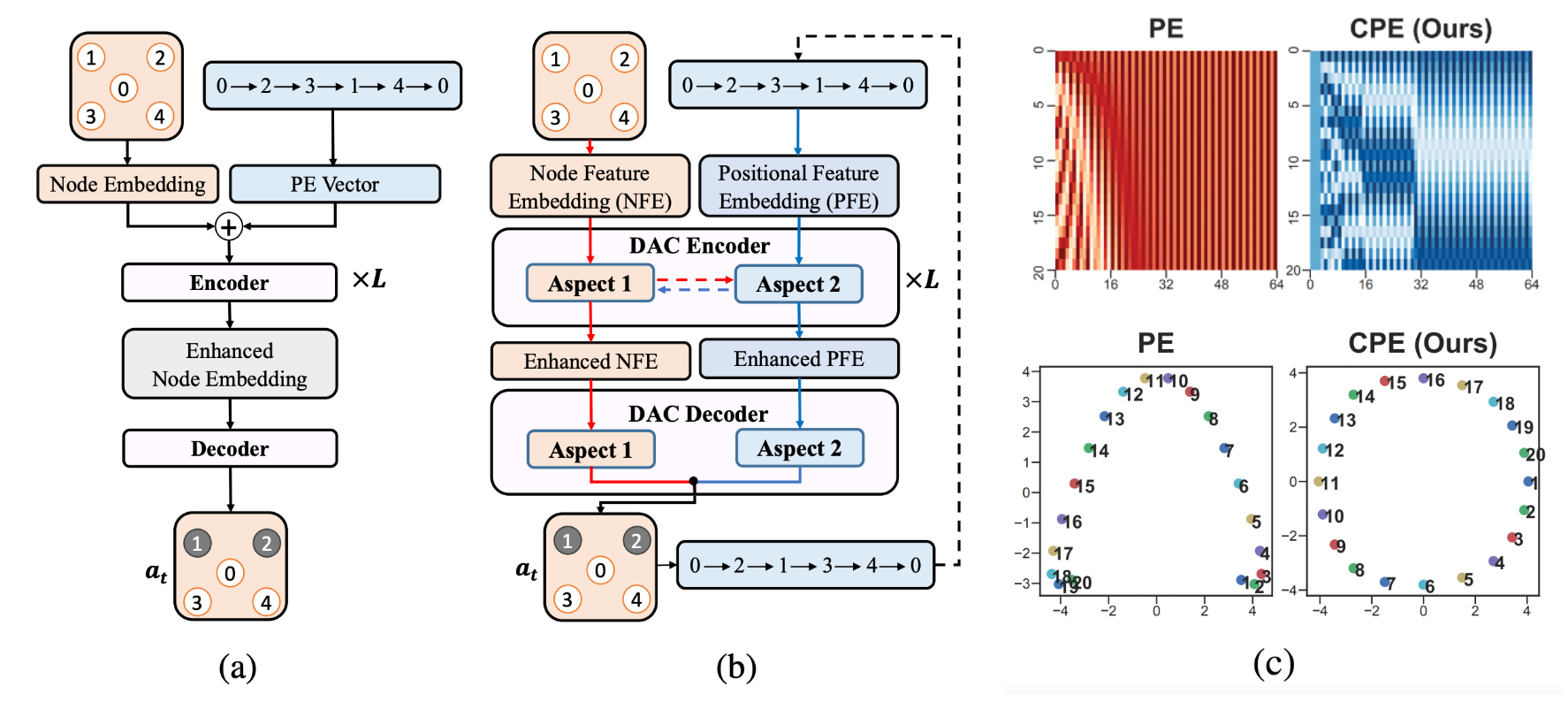
Figure 10: Architectures which learn to improve sub-optimal TSP solutions by guiding decisions within local search algorithms. (a) The original Transformer encoder-decoder architecture [Wu et al., 2021] which used sinusoidal positional encodings to represent the current sub-optimal tour permutation; (b) Ma et al., 2021's upgrade through the lens of symmetry: the Dual-aspect Transformer encoder-decoder with learnable positional encodings which capture the cyclic nature of TSP tours; (c) Visualizations of sinusoidal vs. cyclical positional encodings.
In all these works, since deep learning is used to guide decisions within classical local search algorithms (which are designed to work regardless of problem scale), this approach implicitly leads to better zero-shot generalization to larger problem instances compared to the constructive approaches. This is a very desirable property for practical implementations, as it may be intractable to train on very large or real-world TSP instances.
Notably, NeuroLKH [Xin et al., 2021] uses edge probability heatmaps produced via GNNs to improve the classical Lin-Kernighan-Helsgaun algorithm and demonstrates strong zero-shot generalization to TSP with 5000 nodes as well as across TSPLib instances.
For the interested reader, DeepMind’s Neural Algorithmic Reasoning research program offers a unique meta-perspective on the intersection of neural networks with classical algorithms.
A limitation of this line of work is the prior need for hand-designed local search algorithms, which may be missing for novel or understudied problems. On the other hand, constructive approaches are arguably easier to adapt to new problems by enforcing constraints during the solution decoding and search procedure.
Learning Paradigms that Promote Generalization
Future work could look at novel learning paradigms (pipeline step 5) which explicitly focus on generalization beyond supervised and reinforcement learning, e.g. Hottung et al., 2020 explored autoencoder objectives to learn a continuous space of routing problem solutions.
At present, most papers propose to train models efficiently on trivially small and random TSPs, then transfer the learnt policy to larger graphs and real-world instances in a zero-shot fashion. The logical next step is to fine-tune the model on a small number of specifc problem instances. Hottung et al., 2021 take a first step towards this by proposing to finetune a subset of model paramters for each specific problem instance via active search. In future work, it may be interesting to explore fine-tuning as a meta-learning problem, wherein the goal is to train model parameters specifically for fast adaptation to new data distributions and problems.
Another interesting direction could explore tackling understudied routing problems with challenging constraints via multi-task pre-training on popular routing problems such as TSP and CVPR, followed by problem-specific finetuning. Similar to language modelling as a pre-training objective in Natural Language Processing, the goal of pre-training for routing would be to learn generally useful latent representations that can transfer well to novel routing problems.
Improved Evaluation Protocols
Beyond algorithmic innovations, there have been repeated calls from the community for more realistic evaluation protocols which can lead to advances on real-world routing problems and adoption by industry [Francois et al., 2019, Yehuda et al., 2020]. Most recently, Accorsi et al., 2021 have provided an authoritative set of guidelines for experiment design and comparisons to classical Operations Research (OR) techniques. They hope that fair and rigorous comparisons on standardized benchmarks will be the first step towards the integration of deep learning techniques into industrial routing solvers.
In general, it is encouraging to see recent papers move beyond showing minor performance boosts on trivially small random TSP instances, and towards embracing real-world benchmarks such as TSPLib and CVPRLib. Such routing problem collections contain graphs from cities and road networks around the globe along with their exact solutions, and have become the standard testbed for new solvers in the OR community.
At the same time, we must be vary to not ‘overfit’ on the top n TSPLib or CVPRLib instances that every other paper is using. Thus, better synthetic datasets go hand-in-hand for benchmarking progress fairly, e.g. Queiroga et al., 2021 recently proposed a new libarary of synthetic 10,000 CVPR testing instances. Additionally, one can assess the robustness of neural solvers to small perturbations of problem instances with adversarial attacks, as proposed by Geisler et al., 2021.
Figure 11: Community contests such as ML4CO are a great initiative to track progress. (Source: ML4CO website).
Regular competitions on freshly curated real-world datasets, such as the ML4CO competition at NeurIPS 2021 and AI4TSP at IJCAI 2021, are another great initiative to track progress in the intersection of deep learning and routing problems.
We highly recommend the engaging panel discussion and talks from ML4CO, NeurIPS 2021, available on YouTube.
Summary
This blogpost presents a neural combinatorial optimization pipeline that unifies recent papers on deep learning for routing problems into a single framework. Through the lens of our framework, we then analyze and dissect recent advances, and speculate on directions for future research.
The following table highlights in Red the major innovations and contributions for recent papers covered in the previous sections
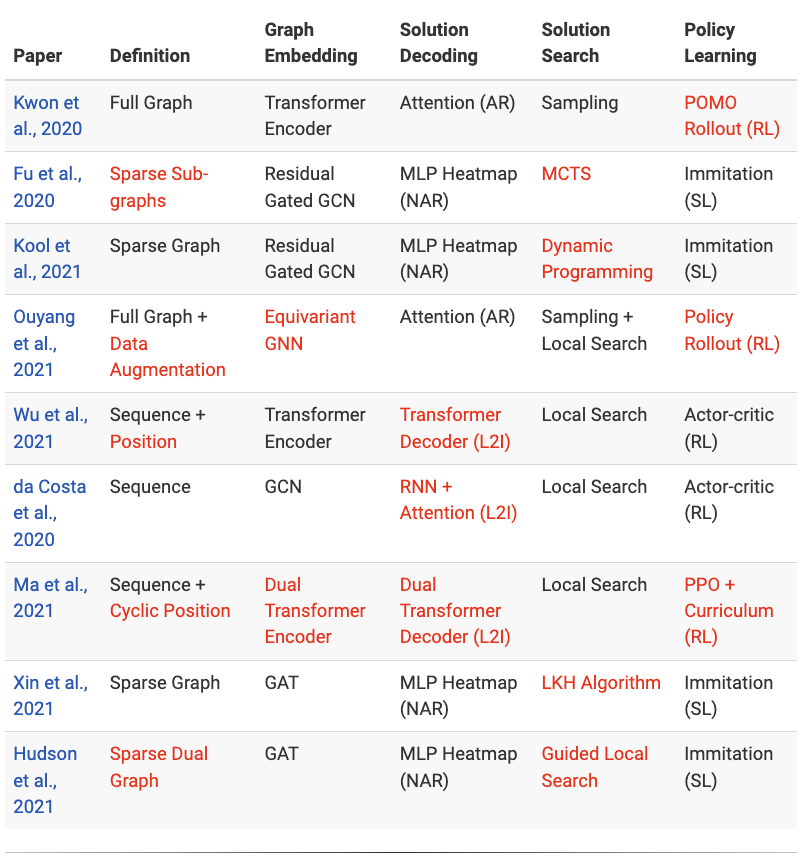
As a final note, we would like to say that the more profound motivation of neural combinatorial optimization may NOT be to outperform classical approaches on well-studied routing problems. Neural networks may be used as a general tool for tackling previously un-encountered NP-hard problems, especially those that are non-trivial to design heuristics for. We are excited about recent applications of neural combinatorial optimization for designing computer chips, optimizing communication networks, and genome reconstruction, and are looking forward to more in the future!
