##[Graph] Dijkstra
다익스트라 알고리즘은 음의 가중치가 없는 그래프에서 최단거리를 구하는 알고리즘이다.
초기에 다익스트라가 구현한 버전은 O(V^2)의 복잡도를 가진다.
원리는 아래와 같다.
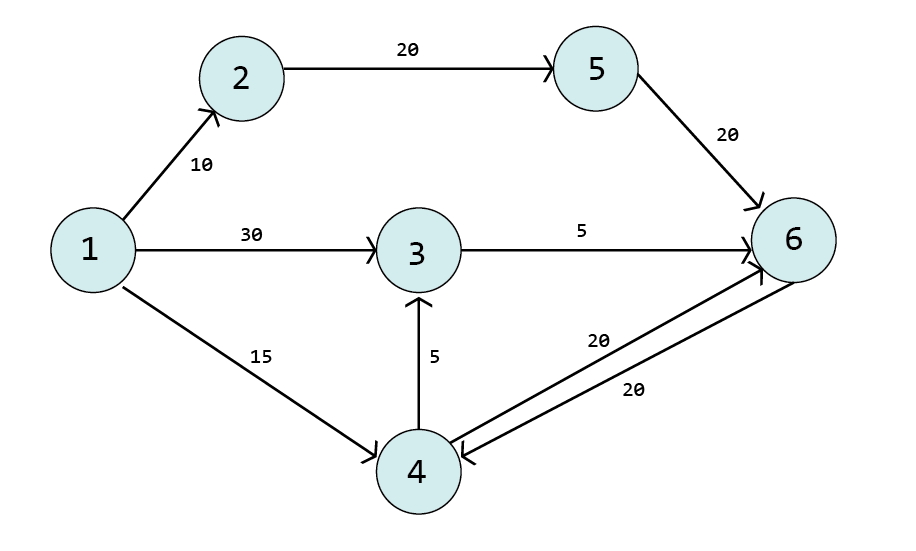
1번 vertex에서 나머지 vertex까지의 최단 비용을 구한다고 가정하자.
#####1.먼저 현재 정점에서 가장 가까운 정점을 선택한다.
#####2.해당 정점을 방문했다고 표시한다.
#####3.해당 정점의 거리를 갱신한다.
여기서 3번 정점을 갱신하는 방법은 1번에서 선택된 정점으로 부터 갈수있는 정점 모두를 갱신한다.
####==인접행렬의 구현 O(V^2)==
#include<iostream>
#include<vector>
using namespace std;
const int INF = 999999;
vector<int> dijkstra(vector<vector<int>>& v, int begin) {
vector<int> d;
vector<bool> visit;
visit.assign(v.size(), false); //모든 정점를 방문하지 않았다고 해야한다.
d.assign(v.size(), INF); //모든 거리를 무한대로 초기화한다.
d[begin] = 0; //시작정점 은 당연히 거리가 0이다.
while(true){
int min = INF;
int s = -1;
//방문하지 않은 정점중에 가장 비용이 적은 정점을 선택한다.
//처음에는 시작 정점이 선택된다.
for (size_t j = 1; j < v.size(); j++)
if (visit[j] == false && min > d[j]){
min = d[j];
s = j;
}
//만일 선택된 정점이 없다면 종료한다.
if (s == -1)break;
visit[s] = true;
//찾은 정점에서 갈수있는 모든정점을 갱신한다.
for (size_t j = 1; j < v.size(); j++)
if (v[s][j]!=-1 && d[j]>d[s] + v[s][j])
d[j] = d[s] + v[s][j];
}
return d;
}
int main() {
vector<vector<int>> v;
v.assign(7, vector<int>());
for (auto& e : v)
e.assign(7, -1);
v[1][2]= 10 ;
v[1][3]= 30 ;
v[1][4]= 15 ;
v[2][5]= 20 ;
v[3][6]= 5 ;
v[4][3]= 5 ;
v[4][6]= 20 ;
v[5][6]= 20 ;
v[6][4]= 20 ;
vector<int> d = dijkstra(v, 1);
for (auto& e : d)
cout << e << endl;
return 0;
}1번째 while 문은 반드시 V번 반복하고, 두번째 for문은 모든 정점을 확인해 보므로 V번 반복한다.
따라서 인접행렬의 경우 시간복잡도는 O(V^2) 다.
####==인접리스트의 구현 O(VE)==
인접 리스트로 구현하면 다중 그래프에서도 다익스트라가 적용된다.
#include<iostream>
#include<vector>
using namespace std;
const int INF = 999999;
struct Edge{
int to;
int cost;
Edge(int to, int cost) {
this->to = to;
this->cost = cost;
}
};
vector<int> dijkstra(vector<vector<Edge>>& v, int begin) {
vector<int> d;
vector<bool> visit;
visit.assign(v.size(), false); //모든 정점를 방문하지 않았다고 해야한다.
d.assign(v.size(), INF); //모든 거리를 무한대로 초기화한다.
d[begin] = 0; //시작정점 은 당연히 거리가 0이다.
while(true){
int min = INF;
int s = -1;
//방문하지 않은 정점중에 가장 비용이 적은 정점을 선택한다.
//처음에는 시작 정점이 선택된다.
for (size_t j = 1; j < v.size(); j++)
if (visit[j] == false && min > d[j]){
min = d[j];
s = j;
}
//만일 선택된 정점이 없다면 종료한다.
if (s == -1)break;
visit[s] = true;
//찾은 정점에서 갈수있는 모든정점을 갱신한다.
//인접 리스트는 이반복문을 더 적게 돌 수 있다.
for (size_t j = 0; j < v[s].size(); j++){
if (d[v[s][j].to]>d[s] + v[s][j].cost)
d[v[s][j].to] = d[s] + v[s][j].cost;
}
}
return d;
}
int main() {
vector<vector<Edge>> v;
v.assign(7, vector<Edge>());
v[1].push_back(Edge(2,10));
v[1].push_back(Edge(3,30));
v[1].push_back(Edge(4,15));
v[2].push_back(Edge(5,20));
v[3].push_back(Edge(6,5));
v[4].push_back(Edge(3,5));
v[4].push_back(Edge(6,20));
v[5].push_back(Edge(6,20));
v[6].push_back(Edge(4,20));
vector<int> d = dijkstra(v, 1);
for (auto& e : d){
cout << e << endl;
}
return 0;
}반면 인접리스트의 경우는 첫번째 while문은 V번 반복하고, 두번째 for문은 E번 반복하므로 시간 복잡도는 O(V*E) 가 된다.
이제 우선순위 큐를 이용하여 조금더 빠른 방법의 다익스트라를 알아보자.
위의 소스에서는 최소비용을 가진 정점을 찾는데 V의 복잡도가 필요했다.
그러나 최소정점을 찾는방식을 우선순위 큐를 사용하면 lgV 시간으로 해결이 가능하다.(삭제시간)
####==인접리스트 + 우선순위큐의 구현 O(ElgE)==
#include<iostream>
#include<vector>
#include<queue> //priority_queue
#include<functional> //greater
using namespace std;
const int INF = 999999;
typedef pair<int, int> pii;
struct Edge{
int to;
int cost;
Edge(int to, int cost) {
this->to = to;
this->cost = cost;
}
};
vector<int> dijkstra(vector<vector<Edge>>& v, int begin) {
vector<int> d;
//<현재거리,정점> 최소힙을 구성
priority_queue<pii,vector<pii>,greater<pii>> pq;
d.assign(v.size(), INF); //모든 거리를 무한대로 초기화한다.
d[begin] = 0; //시작정점 은 당연히 거리가 0이다.
pq.push(make_pair(0,begin));
while (pq.empty()==false){
pii e = pq.top();
pq.pop();
//선택된 최소비용의 정점의 모든 간선을 순회
for (int i = 0; i < v[e.second].size(); i++){
//만일 to의 거리가 현재거리+비용 보다 크다면 거리d 를 갱신
if (d[v[e.second][i].to]> d[e.second] + v[e.second][i].cost){
d[v[e.second][i].to] = d[e.second] + v[e.second][i].cost;
//갱신된 거리와 해당정점을 우선순위큐에 push
pq.push(make_pair(d[v[e.second][i].to], v[e.second][i].to));
}
}
}
return d;
}
int main() {
vector<vector<Edge>> v;
v.assign(7, vector<Edge>());
v[1].push_back(Edge(2,10));
v[1].push_back(Edge(3,30));
v[1].push_back(Edge(4,15));
v[2].push_back(Edge(5,20));
v[3].push_back(Edge(6,5));
v[4].push_back(Edge(3,5));
v[4].push_back(Edge(6,20));
v[5].push_back(Edge(6,20));
v[6].push_back(Edge(4,20));
vector<int> d = dijkstra(v, 1);
for (auto& e : d){
cout << e << endl;
}
return 0;
}우선순위큐를 사용하게 되면 각정점마다 인접한 간선들을 모두 검사하는데 O(E)
우선순위 큐에 원소를 넣고 삭제하는데 걸리는 시간 O(lg V) (정점들이 우선순위 큐에 들어가므로)
그러나 거리d를 갱신할때 중복되에 큐에 들어갈 수 있다. 따라서 정점의 개수 V보다 좀더 우선순위 큐에 들어갈 수 있다.
이때 정점이 갱신되는것은 간선마다 한번씩 만 갱신되므로 최대 E번 우선순위 큐에 들어갈 수 있다.
우선순위큐의 삽입과 삭제를 고려하면 복잡도는 O(E lgE) 가 된다.
앞서말한 간선검사 시간과 합하면 Tn(E + ElgE) 이므로 O(ElgE) 가 된다.
####명심하자, 우선순위큐를 사용하여 다익스트라를 구현하면 복잡도는 O(ElgE)가 된다.
그런데 보통 간선의 개수 E는 정점의 제곱 V^2 보다 작기 때문에 Tn(E 2lgV) 가되며 O(ElgV) 가 상한이 된다.
####왜 정점들중에 최소값을 먼저 찾는가?
그 이유는 아래의 그래프를 보면 알 수 있다.

비용이 큰 정점부터 계산하게되면, 비용의 갱신이 더 많이 발생하기 때문이다.
비용의 갱신은 곧, 새로운 큐에 삽입하는것을 의미하기 때문에, 작은 비용인 정점부터 찾는것이다.
####우선순위 큐의 단점. 중복
우선순위큐로 다익스트라를 구현하면, 중복된 정점이 삽입될 수 있다. 이때 기존의 정점은 제거를 해야하는데 우선순위큐의 자료구조 특성상 그럴수가 없다.
따라서 트리를 사용하게 되면 중복된 정점을 제거할 수 있어, 더 빠른 연산이 가능하다.
앞서 말한 큐에 정확하게 V의 개수가 삽입되기 때문에, 시간복잡도는 O(VlgV) 가 될 수 있다.
아래의 코드는 red/black을 기반을한 C++ std::set을 이용하여 다익스트라를 구현하였다.
####==인접리스트 + 레드블랙트리 구현 O(VlgV)==
#include<iostream>
#include<vector>
#include<set>
#include<functional> //greater
using namespace std;
const int INF = 999999;
typedef pair<int, int> pii;
struct Edge{
int to;
int cost;
Edge(int to, int cost) {
this->to = to;
this->cost = cost;
}
};
vector<int> dijkstra(vector<vector<Edge>>& v, int begin) {
vector<int> d;
set<pii> pq; //삭제가 가능한 트리로 구성
d.assign(v.size(), INF); //모든 거리를 무한대로 초기화한다.
d[begin] = 0; //시작정점 은 당연히 거리가 0이다.
pq.insert(make_pair(0,begin));
while (pq.empty()==false){
pii e = *pq.begin(); //트리의 제일 작은값을 가져옴
pq.erase(e);
//선택된 최소비용의 정점의 모든 간선을 순회
for (int i = 0; i < v[e.second].size(); i++){
//만일 to의 거리가 현재거리+비용 보다 크다면 거리d 를 갱신
if (d[v[e.second][i].to]> d[e.second] + v[e.second][i].cost){
//기존 정점을 제거하고 더 비용이낮은 정점으로 교체
pq.erase(make_pair(d[v[e.second][i].to], v[e.second][i].to));
d[v[e.second][i].to] = d[e.second] + v[e.second][i].cost;
pq.insert(make_pair(d[v[e.second][i].to], v[e.second][i].to));
}
}
}
return d;
}
int main() {
vector<vector<Edge>> v;
v.assign(7, vector<Edge>());
v[1].push_back(Edge(2,10));
v[1].push_back(Edge(3,30));
v[1].push_back(Edge(4,15));
v[2].push_back(Edge(5,20));
v[3].push_back(Edge(6,5));
v[4].push_back(Edge(3,5));
v[4].push_back(Edge(6,20));
v[5].push_back(Edge(6,20));
v[6].push_back(Edge(4,20));
vector<int> d = dijkstra(v, 1);
for (auto& e : d){
cout << e << endl;
}
return 0;
}