[PS] [DP] weighted interval scheduling

WIS 라 불리는 가중치를 가진 구간 문제이다.

n개의 구간이 있고

각 구간마다 가중치(weight)를 갖는다.

겹치지 않게 구간을 선택하는데 , 가중치의 합이 가장큰 구간들을 고르는 문제이다.

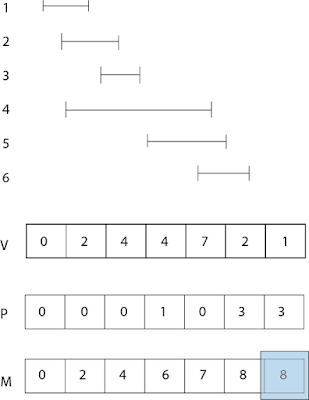
1~6의 6개의 구간이 있다.

먼저 끝 구간을 기준으로 정렬을 한다.

V는 각 구간의 가중치이다. V,P,M 모두 0번째는 0으로 초기화를 한후 1부터 시작한다.

간단하게 V 배열을 채울 수 있다.

P는 non overlapping interval (right most value) 이다.

겹치지 않는 앞의 구간중 가장 오른쪽에 있는 구간 을 뜻한다.

P[3] 은 1인데, 3번 구간은 1번구간과 겹치지 않기 때문에 1이다.

P를 다르게 말하면, P[i]는 i 번째 구간까지 있을때,

i번째 구간과 겹치지 않는 가장 마지막 구간을 뜻한다.

설명이 어려운데, 잘 알아먹길 바란다.

M은 이제 위에서 구한 V와 P를 가지고 정답을 계산하는 배열이다.

공식 부터 보자
for i is 1 to N+1
do M[i]=max( V[i] + M[ P[i] ] , M[i-1]);

M[i] 는 현재 구간의 가중치 + 현재 구간이전 구간중 현재 구간과 겹치지 않는 구간까지의

선택중 가장 최상의 선택의 가중치

와

이전 구간까지의 최상의 선택 가중치

중

큰 값이다.

그림을 그려서 보면 이해가 잘 될 것이다.

가장 마지막에 계산한 M[n] 이 답이된다.

복잡도는 정렬시 nlogn

V계산에 n

P계산에 nlogn ( 이진탐색으로 P[i] 를 찾음)

M계산에 n

으로 nlogn에 답을 구할 수 있다.