[PS] Daejeon 4846 Mines

본 문제는 지뢰를 터트리는데, 최소한 으로 터트려야하는 개수를 출력하면된다.

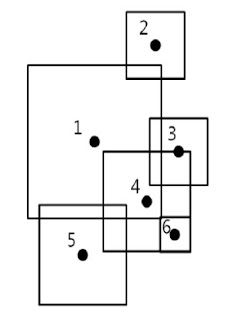
다음과 같이 지뢰가 있을때, (1) 을 터트리면 (4)도 터지게 되고 (3),(6)도 터지게 된다.

그리고 (2)와 (5)를 각각 터트려야한다. 따라서 위 예시의 답은 3이다.

처음에는 DFS를 이용하여 연결된 정점들을 모두 찾아 하나로 묶어 묶어진 개수를 출력

하게 짰으나 Wrong Answer가 나오게 되었다.

그 예시가 하나의 정점 V1 에 대해 그 정점을 가르키는 정점이 2개 이상일 경우이다.

따라서 본문제는 SCC를 모두 구하고 각 SCC의 시작점의 개수를 출력하면된다.

위 예시에서 SCC는 6개이고 각 SCC의 루트는
1->1
2->2
3->1
4->1
5->5
6->1

으로 시작점의 개수가 1,2,5 이렇게 3개가 된다.

단순히 scc알고리즘으로 푸는것 보다는 tarjan 알고리즘을 이용해 푸는것이 더 효율적이다.

방문한 순서를 저장하고, 각 scc의 root를 저장하고, 방문하였는지를 체크하도록 하여

DFS를 구현하면된다.

또한 그래프를 인접행렬로 만들시, 단순히 N^2으로 그래프를 생성하지않고

x축 기준으로 정렬한뒤, lower_bound와 upper_bound를 찾아 미세조정을 한뒤

그 구간만 검사하면, C*nlogn 으로 그래프생성을 할수있다.

따라서 본 문제의 복잡도는 O(nlogn + V + E) 이다.