02/14~
게임에서의 벡터, 행렬, 내적, 외적의 활용, 회전 잘 모르는데,
최대한 배워보기두 사각형 영역 AABB의 겹침을 판정하는 함수의 작성
(구조체의 멤버함수)
늘 작업한 코드를 빌드하고 게임을 실행했는데,
어제까지 정상적이던 프레임율(Frame Rate)이 떨어지는 상황이 발생했다.
이의 원인을 찾고 해결하기 위한 자신만의 대처법게임 제작에서 이동, 크기, 회전으로 구성된 트랜스폼을 사용해 물체를 변환할 때
변환 순서를 올바로 기술한 것을 고르시오.
위의 내용들이 오늘 해야할 것들이다.
수포자를 위한 게임 수학
수포자는 아니지만, 위의 강의를 보고 대략적인 개념을 파악하고,
심화학습을 하려고 한다.
선형대수학
선형적인 공간에서 일어나는 대수를 다루는 학문
숫자가 아닌 숫자를 대신하는 수를 대수라고 한다.
3 * 5 = 15 이런건 대수를 사용한 식이 아니고,
PlayerMoveSpeed = OrignSpeed * Accel
이런게 대수들이라고 한다.
선형은 y=x같은 그래프의 선형적인 공간이고,
선형공간은 각 원소를 서로 더하거나, 늘리거나 할 수 있는 공간이다.
유클리드공간이라는 개념도 나오는데,
유클리드의 거리길이각도에 대한 좌표계를 도입하여
평면과 공간을 일반화한 것이다.
직교하는 x,y,z축으로 구성된 공간이고, 선형공간이다.
이 공간에서 벡터 등등 사용된다.
벡터
벡터는 크기와 방향이 존재한다.
크기는 속도의 의미로 다르게 해석될 수도 있다.
벡터는 (x,y) 좌표로 하나로 표시되는데,
벡터는 시작과 끝이 존재하지 않지만, 암묵적으로 0,0에서
해당 x,y로 이어지는 화살표의 형태로 본다.
그래서 크기와 방향을 표시한다.
x,y,z라면, 3차원 벡터
유니티의 transform에서 position은 3차원 벡터를 의미한다.
덧셈
벡터에 덧셈이 존재.
각 요소끼리 더해주면 된다. (3,4) + (8,9)라면
(11,13)으로 계산하면 된다.
그림으로 그린다면, 2개의 벡터 각각을 평행으로 이동시킨 평행사변형모양을 그리면 된다.
뼬셈도 똑같다. 요소끼리 빼면 된다.
사실 덧셈과 같다. A-B벡터라는 것은, A+(-B)벡터라는 것과 같기에,
B의 요소를 -한 -B벡터와 A벡터의 합연산을 한 평행사변형을 그리면 된다.
크기
벡터는 크기와 방향이 존재한다고 했다.
크기는 피타고라스 정리를 사용하여 쉽게 구하면 되고,
||V||이런식으로 작대기를 2개씩 그어서 표현한다.
그냥 작대기 하나로 표기하기도 한다.
(a^2+b^2)^1/2 = ||V||
단위화
벡터를 단위화한다는 것은, 벡터의 크기를 1로 만들어서
방향만을 사용하고 싶은 경우 사용한다.
방법은, 원래 벡터 x,y의 크기를 구하고,
(x/||V||, y/||V||) 각 요소를 크기로 나누는 연산을 취하면 된다.
위 기능들은 자주쓰여서
- Vector2, Vector3 이런식으로 벡터의 자료형
- 덧셈 뺄셈의 구현
- v.normalize - 단위화
- v.magnitude - 벡터의 크기
유니티에선 위처럼 기본적으로 구현이 되어있다.
Me에서 Target의 위치로 이동하려면 어떤 연산을 해야할까

먼저 Target벡터에서 Me벡터를 빼면된다.
Target-Me이므로, Me의 -Me벡터인 핑크색 벡터를 구하고,
해당 핑크벡터와 하늘색 Target벡터의 합연산을 하면,
초록색 벡터가 나오는데,
해당 Me에서 해당 초록색 벡터를 더하면, Target이 된다.
즉,
Me+(Target-Me)를 하면 Me에서 Target으로 이동이 가능하다.
void Update(){
Vector2 green = target.position - me.position;
green.Normalize();
green *= speed * Time.deltaTime;
me.position += green;
}위와 같은 식을 사용하여, me에서 green벡터의 방향으로 speed만큼
천천히 이동하는 식을 만든 것이다.
여태까지 당연하게 쓰던 positon이 벡터를 의미했던게 소름돋았다.
PI
PI를 알아야, 라디안을 이해할 수 있고, 삼각함수를 이해할 수 있고, 내적을 이해할 수 있게 된다고 한다.
내적을 이해해야만 벡터를 이해할 수 있다.
PI란 뭔가?
원주율 - 원의 지름에 대한 원의 둘레의 비로,
원에 내적하는 도형을(6각형과 12각형) 그린다음, 피타고라스 정리로 계산을 하다보면,
점점 해당 직선의 길이를 곡선과 비슷하게 보일정도로 세분화하면서
계산해서 나온것이 3.14
간단히 원주/지름을 PI라고 본다.
라디안
실생활에서 각도는 360도까지 사용을 하는데, (넘어갈 순 있다 의미가 없을뿐)
이런 방법을 60분법이라고 하고,
유니티에서도 Rotation은 같은 방법을 사용한다.
수학에선 호도법을 사용하기도 하고, 라디안이라고도 불리운다.
호도는 원의 호를 통해서 나타내는 각도를 의미한다.
호의 길이가 길수록 큰 각도, 짧을수록 작은각도를 의미한다.
세타는,
반지름이 1이고, 호의 길이가 1인 해당 각도를 1라디안이라고 부르고,
세타라는 표준으로 잡았다.
1라디안 == 1세타 애매한 개념 일단 스킵
PI를 원주/지름 = PI라고 했었는데,
1라디안을 표현하기 위해선, 반지름을 기준으로 판단을 해야하는데,
이를 위해서 분모분자에 각각 1/2를 곱해주면,
PI = 반원주/반지름으로 식을 응용할 수 있겠고,
반지름이 1인 원의 기준으로는, 그냥 PI = 반원주가 되는 것이다.
라디안 각도 표기 방식에서,
각도는 원의 호로 표시한다고 했는데,
반원주라는 것도 호기 때문에,
해당 반원주가 표현하는 각도는 180도 일 것이다.
그렇기에 PI는 라디안에서 180도를 의미한다.
그렇다면 자동으로 2PI는 360도가 된다.
그렇다면 자동으로 1/2PI는 90도가 된다.
1도라는 것은, PI/180일 것이다.
더 나아가서, 호의 길이가 1인 해당 각도를 1라디안으로 보았는데,
호의 길이가 PI인 것을 180도로 보았으므로,
1 : 1rad = PI : 180이고, 1rad x PI = 180에서
1rad = 180도/PI로 식이 만들어진다.
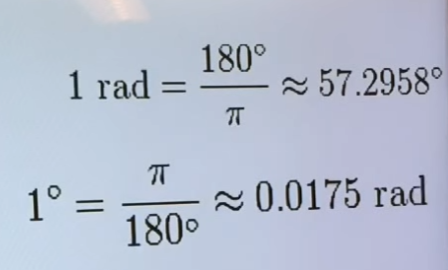
위처럼 라디안을 60분법으로,
60분법을 라디안으로 변환할 수 있다.
이것도 워낙 많이 쓰이기 때문에, 유니티에서 지원한다.
60분법을한 각도를 Degree라고 한다, 호도법은 Radian
- Mathf.Rad2Deg - R to D
- Mathf.Deg2Rad - D to R
SIN / COS
반지름 1인 원을 그리고, 세타라는 일정 각만큼 각도를 정하고,
해당 반지름을 빗변으로 하는 직각삼각형을 그렸을 때,
각 변은 cos, sin 세타로 표기할 수 있게 된다.
해당 세타의 값의 변환에 따른 그래프를 만들 수 있게 된다.
sin을 y축으로, cos를 x축으로 하면
원이 그려진다고 한다.
반지름 1인 원에서 그린 직각삼각형의
각 변은 cos, sin 세타로 표기할 수 있게 된다라는 말에서,
해당 원 위에서의 꼭짓점의 좌표는 (cosT, sinT)로 표현할 수 있을 것이다.
세타를 T로 본다.
같은 원리로 tanT = sinT / cosT로 본다.
플레이어 객체의 velocity를 얻어와,
방향만 추출하고, 해당 방향에 따른 atan(아크탄젠트) 연산을 통해,
해당 값만큼 rotation한 예제이다.
벡터의 내적
벡터의 곱셈은 내적과 외적이라는 2가지 방식이 있다.
벡터의 내적은 벡터의 곱셈이고,
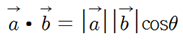
위처럼 내적임을 표시하기 위해서 점을 표시한다.
그리고 각 요소끼리 곱한다.
AxBx + AyBy 2차원벡터
벡터의 내적은, 벡터간의 투영 길이를 나타낸다.
벡터의 내적은 두 벡터간의 각도를 얻어올 수 있는 방법이 되기도 한다.
쉐이더에서 빛을 보는면, 빛을 등진면 같은 두 효과에서도 사용된다.
벡터의 내적은 교환법칙이 성립한다. 계산하는 두 벡터 요소가 두 식이 동일하다면 값도 그냥 같다. cos도 같을거니깐
제1코사인법칙
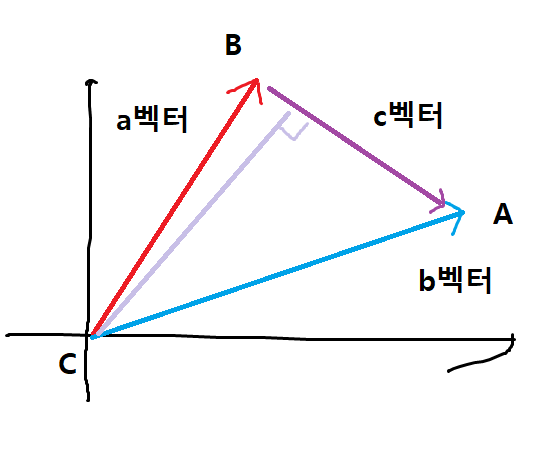
변 AB의 길이(c벡터의 크기)는 어떻게 되는가이다.
c = a cosB + b cosA일 것이다. c는 벡터가 아니고 벡터의 크기이다.
c벡터를 해당 직교를 기준으로 2개의 직각삼각형으로 나눠서 보았을 때,
cosB는, c벡터의 짧은 부분 / a벡터의 크기일 것이고,
여기에 a벡터의 크기를 곱한다면, 해당 부분만 남게 된다.
이런식으로 나머지도 더해서 계산.
제2코사인법칙
1법칙에서 c = a cosB + b cosA였다.
그렇다면 같은 원리로,
a = b cosC + c cosB
b = a cosC + c CosA로 표시할 수 있다.
그리고 각각을 c,a,b를 양변에 곱해서 제곱의 형태로 만들고
식을 가지고 이것저것 조리하면,
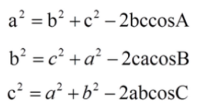
위와 같은 식이 나온다.
벡터의 내적의 공식은 제2코사인법칙을 활용하여 만든다.
내적은 벡터끼리의 곱셈이지만, 값은 스칼라값이 나온다.

a,b의 길이가 1인 벡터라면,
해당 세타의 값이 0이면 1이 나오고,
90이면 0,
180이면 -1이라는 값이 나오게 된다.
그 이유는 그냥 cosT의 값만 남기 때문이다.
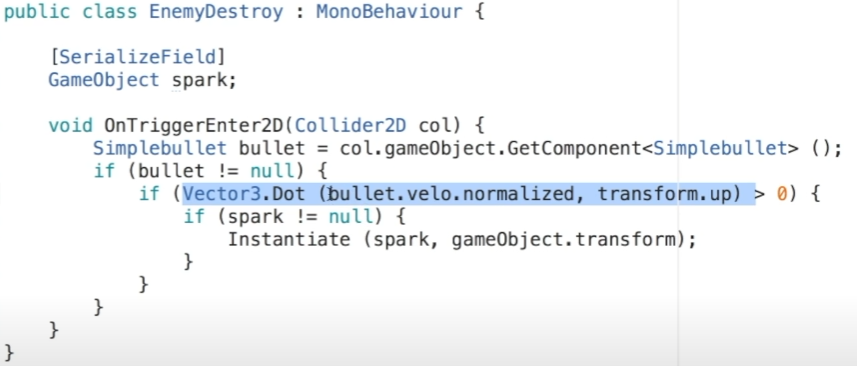
실제 예제
적의 앞부분에는 싈드가 있어서 총알로 때리지 못하는 예제
위에서 Dot이 벡터의 내적연산인데,
총알이 바라보는 방향(단위벡터)와 적이 바라보는 방향을 내적을 해서,
이 값이 0보다 크면 코드를 진행하는 것인데,
두 단위벡터의 내적이 0보다 크다는 말은, 방향이 90도거나, 같은 방향을 보는 그 사이의 각도를 의미한다.
같은 방향을 본다는 것은, 총알의 입장에선 적의 뒤를 보고있다는 의미이므로,
spark라는 게임 오브젝트를 띄워주는 예제이다.
벡터의 내적2 - 이게 핵심
벡터의 내적에는 2개의 공식이 있었다.
 위같은 식과,
위같은 식과,
AxBx + AyBy
위같은 식이 있었다.
그래서 a와 b의 크기가 1이라면,
1번째 공식에 의해서 cosT가 내적의 결과인 스칼라 값이 될 것이다.
내적이 쉐이더에서 빛처리에 주로 쓰인다고 했었다.
그리고, 벡터의 내적은 다른 벡터에 투영을 하는 것이라는 개념도 있다고 했다.
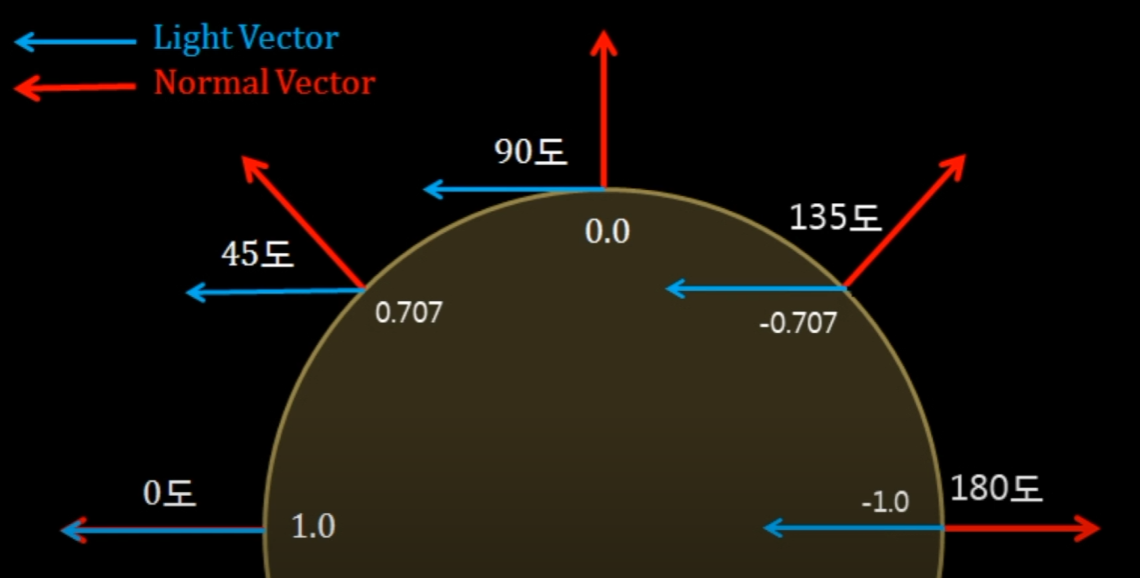
위의 그림을 보았을 때,
파란색 light벡터와,
구체의 면에 수직으로 대응되는 빨간색 normal벡터가 존재할 때,
내적한 값을 표시한 것이고, 1이면 밝고, -1이면 어두운 명암을 의미한다.
램버트쉐이딩 방식이고, -1~1까지의 범위이고,
half램버트쉐이딩이라는 1~0까지의 범위를 가진 쉐이딩도 있다고 한다.
아무리봐도 그림이 이해가 되지 않는다.
light벡터가 우에서 좌로 가는 방향벡터라는 의미가 맞다면..
가장 오른쪽의 180도의 벡터는 가장 밝은 면이지만, 가장 어두워야 할 것이다
[이걸보고 드디어 해결했다]
당연히 실제 조명light의 방향과, normal의 방향이 반대여야
가장 최고의 밝기를 가질 수 있을 것이다.
그런데 내적도 빛의 방향대로 하면 내가 원래 생각했던 것과 같이 반대의 결과가 나오므로,
그냥 내적만해도 편하게 결과를 내기 위해서,
암묵적으로 빛의 방향을 반대로 생각하여 계산한다.
그러면 위처럼 1, -1까지의 값이 자연스레 나오게 된다.
그리고, 해당 각도에 따라 에너지보존법칙에 따라,
각도가 기울어지면 빛을 받는 면이 넓어지고, 그만큼 빛도 분산되어야하는데,
그냥 cosT로 계산하면 된다고 한다.
행렬
행 ㅡ
렬 ㅣ

A라는 행렬은, m개의 행과, n개의 열로 이루어져 있다.

transform은 보면 SRP가 따로따로된 것처럼 보이지만,
내부적으로는 한 묶음의 행렬로 표현한다.
다른 3D엔진도 마찬가지이다.

S R T 모두 다 행렬의 곱연산으로 변환이 이루어지는데,
상당히 복잡해보이지만, 각 연산은 벡터의 내적이다.
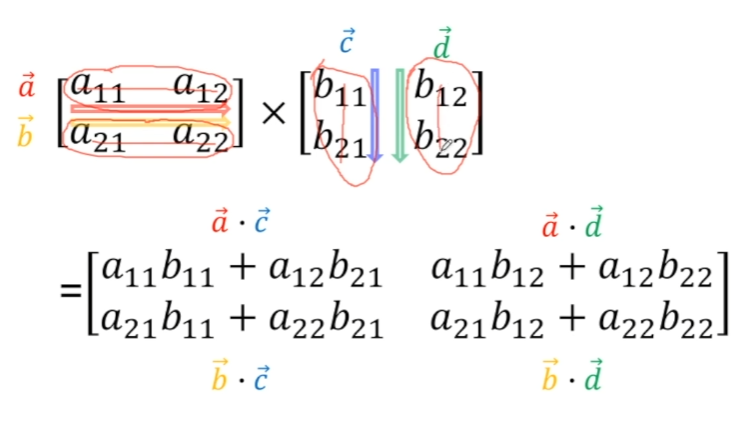
첫 행렬의 2행을 각 벡터로보고, 두번째 행렬의 2열을 각 벡터로 본다음,
해당 방법대로 내적계산을 하면 된다.
각 원소를 x,y라고 보고, AxBx + AyBy 이 연산처럼 수행하면 되는 것이다.
행렬과 벡터
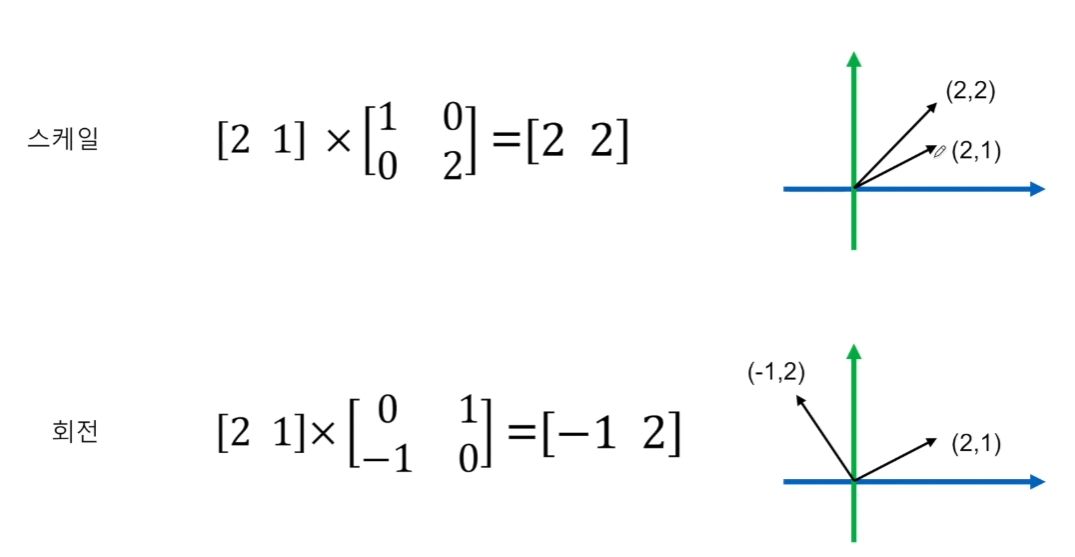
벡터 2,1을 행렬로 표현할 수 있다.
1행 2열의 [2 1]로 표현이 가능했고,
벡터의 크기를 [2 2]로 크기를 키우기 위해서
뭔가를 곱연산을 해야하는데,
(S R T 모두 다 행렬의 곱연산으로 변환이 이루어진다.)
2x2행렬이 와야한다는 것을 본능적으로 알 수 있을 것이다.
회전도 마찬가지로 같은 방식으로 계산한다.
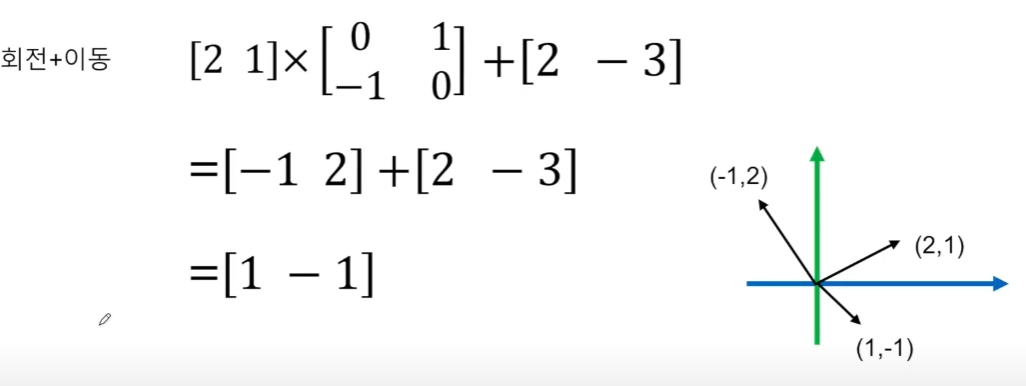
회전과 이동인데, 이동은 +연산이다.
각 원소를 더하기만 하면 된다. 벡터의 연산과 같다.

회전과 이동을 한 번에 처리하기 위해 위처럼 행렬이 보이는데,
한번에 하기 위해선, 해당 벡터의 차원에 +1을 해줘야 한다.
그러면 4열이 최대겠다
그래서 2D벡터이므로 3열로 늘렸고,
뒤 행렬도 계산하려면 3x3으로 늘려야했고,
나머지 부분은 그냥 001로 처리해서 1로 강제적으로 나오도록 표기를 했다.
회전 부분에 스케일도 포함이 되게 할 수 있다
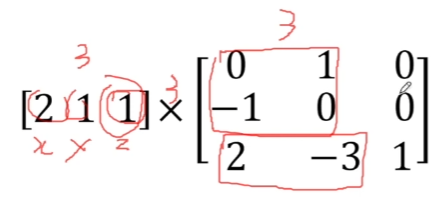
위의 2x2가 회전을 담당했던 부분이고,
아래 1x2가 이동을 담당했던 부분이고,
결과가 1,-1,1로 나오는데, 앞의 2개의 요소로 값을 판단한다.
행렬과 벡터2

위의 transform을 표현하기 위해서 한묶음의 행렬로 구성되어있다고 했다.
그 크기는 3차원벡터기에 4x4임을 이제는 알 수 있다.
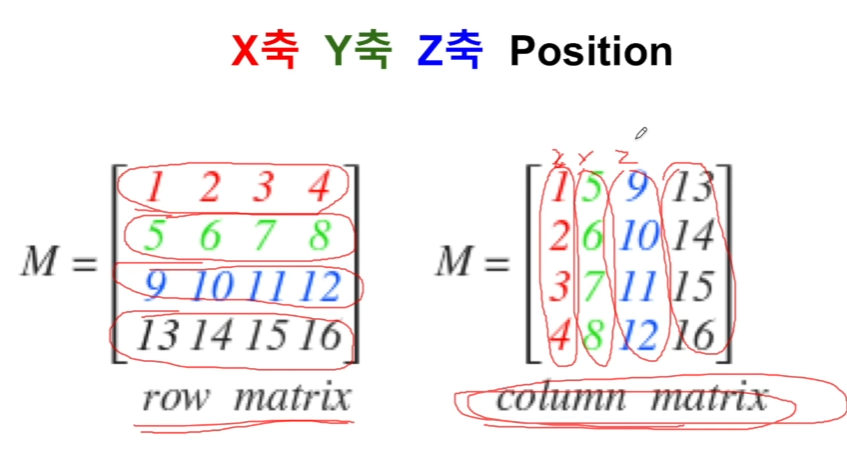
행렬을 표현하는 방식이 하나는 아니다.
15913을 하나의 벡터로 보는 엔진이 있기도 하다.
유니티는 열기준이지만,
언리얼은 행기준행렬이다.
각 방식에 맞게 순서대로 x,y,z축을 의미한다.
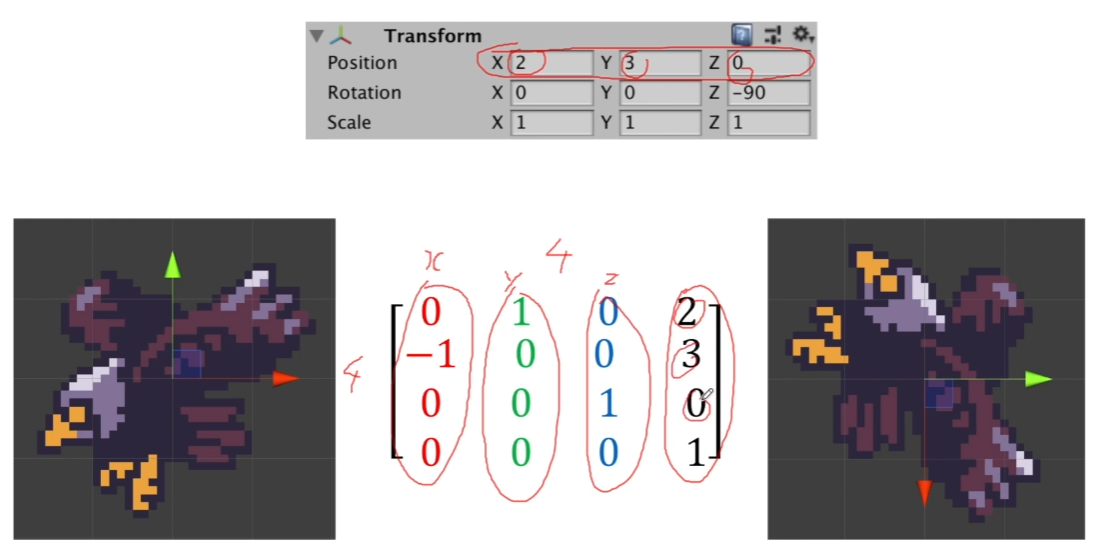
유니티 기준 설명이다.
각 세로 열들이 x,y,z축 그리고 position을 의미하고,
각 축들의 행들은 또다시 x,y,z축으로의 값을 의미한다.
각 축들의 마지막은 그냥 0으로 채운 것이다.
Rotation과 Position을 위주로 보자.
회전한 독수리에 대한 행렬인데,
x축의 y부분에 -1 ,y축의 x부분에 1, z축의 z부분에 1로 표시되어있다.
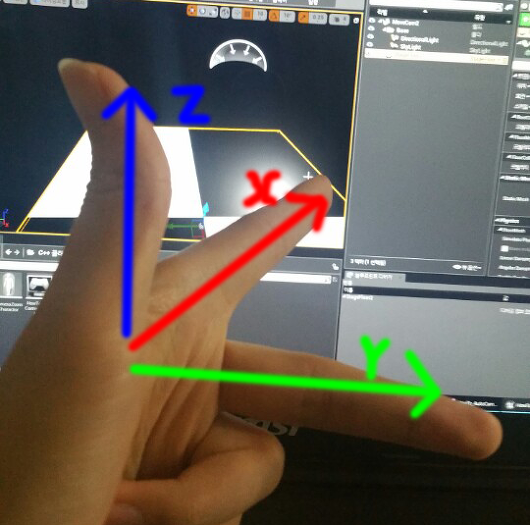
그림에서 초록화살표가 y축이고, 빨강화살표가 x축인데,
-90만큼 즉, 오른쪽으로 돌렸다는 것은,
x축이 y축위에서 -1을 가리키고,
y축이 x축위에서 1을 가리킬 것이므로 위처럼 표시가 된다.
position은 2,3,0 그대로 가져오고
마지막 1은 국룰인듯 하다.
이를 언리얼의 행기준 행렬로 변환한다면,
원래의 독수리는
x 1 0 0 0
y 0 1 0 0
z 0 0 0 1
p 2 3 0 1회전후의 독수리는
x 0 -1 0 0
y 1 0 0 0
z 0 0 1 0
p 2 3 0 1 위처럼 될 것이다.
3x3의 행렬에서 R과 S를 담당할 것이고,
마지막 P의 행 혹은 열에서 위치를 담당하게 되는 것이다.
행렬과 벡터3
행기준 행렬에서의 곱연산을 해봤었다.
행기준에서는 V라는 1행짜리 벡터와 해당 열에맞는 nxn의 M 행렬과의 곱을 했다.
열기준 행렬에서의 연산은 다르다고 한다.
행렬의 곱에 있어서, A*B와 B*A의 결과는 다르다고 한다.
행기준이 VM으로 곱했다면,
열기준은 MV 방식으로 곱한다.
행렬과 벡터4

z축으로 세타만큼 회전시키는 행렬에 대해서 본다.
우선

위의 공식을 외워두어야 한다.
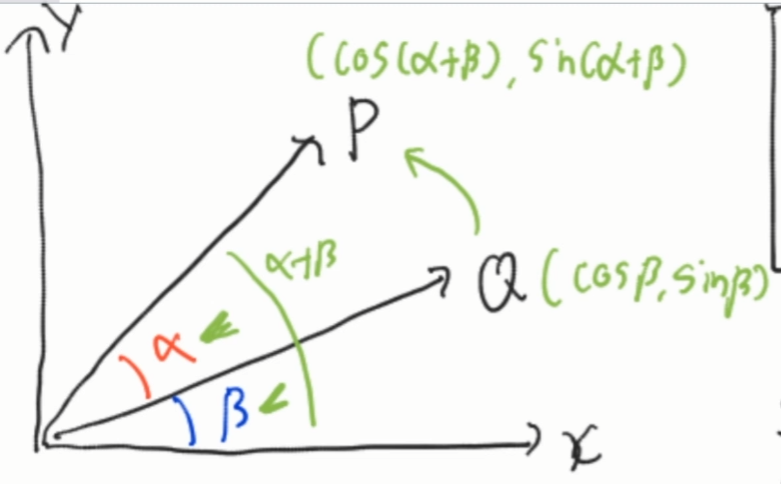
Q에서 Q만큼 회전하고 싶다고 할 때,
이건 Z축의 회전이다.
각각 사잇각을 알파, 베타라고 본다면,
P와 Q의 좌표를 위처럼 표현할 수 있을 것이다.
P를 덧셈정리에 의해 세부적으로 다시 분해해볼 수 있게 된다.
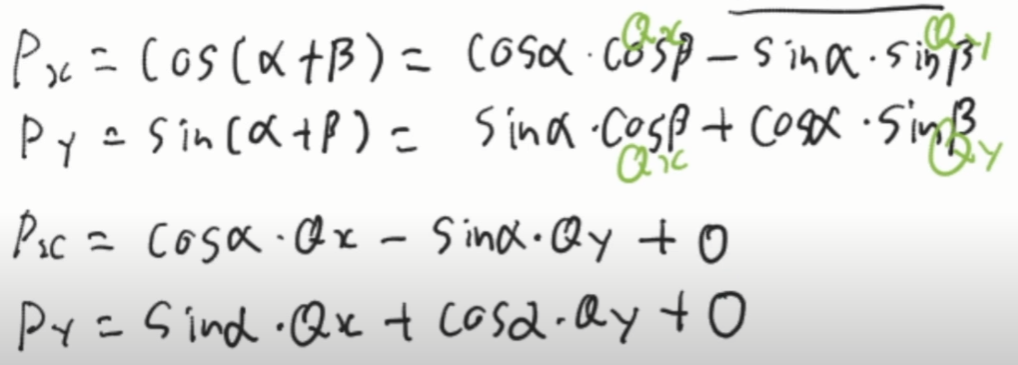
위처럼 표현이 가능하고, 이를 행렬과 벡터의 곱셈식처럼 본다면,
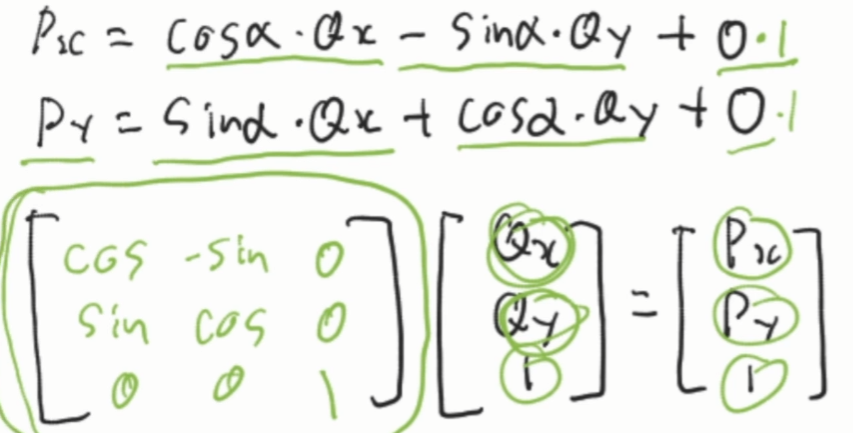
이렇게 볼 수 있을 것이다.
2차원을 기준으로 한 것이라 3차원 행렬을 곱하는 것이다.
3차원은 4차원 행렬이고 훨씬 복잡해진다.
좌표계
유니티와 언리얼 모두 왼손좌표계를 사용한다.
하지만 같은 왼손좌표계라도 위처럼 다르게 해석할 수 있다.
유니티에서의 x,y는 세로로된 평면 상에서의 x,y이고,
마인크래프트 같다, y가 -54부근 높이에서 다이아가 잘 나온다.
언리얼에서의 x,y는 가로로된 평면 상에서의 x,y이다.
언리얼에서의 높이는 z축으로 담당하게 되는 것이다.
행렬의 형태
[ 행렬의 종류 ]
1. 전치행렬
2. 직교행렬
3. 단위행렬
4. 정방행렬
5. 역행렬
위의 각 행렬마다 쓰임새가 있어서 이름도 붙여지고 네임드화된 행렬이다.
- 전치행렬 - 행렬

행기준인 언리얼엔진의 경우, 행렬이 M처럼 표시가 되는데,
이런 행렬을 전치행렬했다는 것의 의미는,
행기준을 열기준처럼 바꿨다는 의미가 된다.
열기준을 행기준처럼 바꾼것도 성립
- 직교행렬
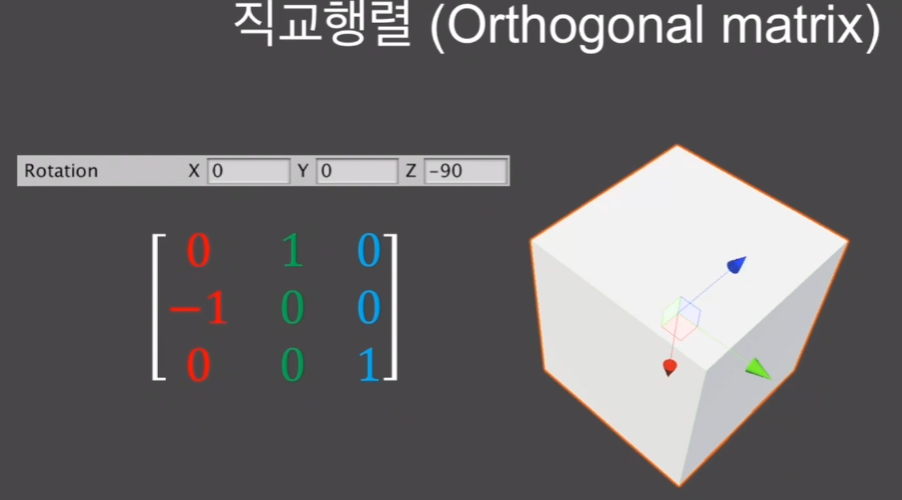
행렬에서 x,y,z축 부분을 보았을 때,
각각 다른 축에 위치해있으면, 그대로 90도 위치에 서로 있는 것이므로
각 열끼리 90도를 유지하고 있는 행렬을 직교행렬으로 본다.
행기준이면 각 행끼리
- 단위행렬 / 항등행렬
단위행렬이라고 많이 말하고,

위처럼 대각선 부분만 1인상태를 단위행렬이라고 하는데,
처음 유니티에서 3D객체를 만들면 transform의 상태와 같다.
각 열은 각 축을 의미할 것이고, 마지막 1은 그냥 있는 1이겠다.
- 정방행렬
행과 열의 개수가 같은 행렬을 의미
그냥 2x2, 3x3, 4x4, 5x5 이런 큰 범위의 정의이다.
- 역행렬
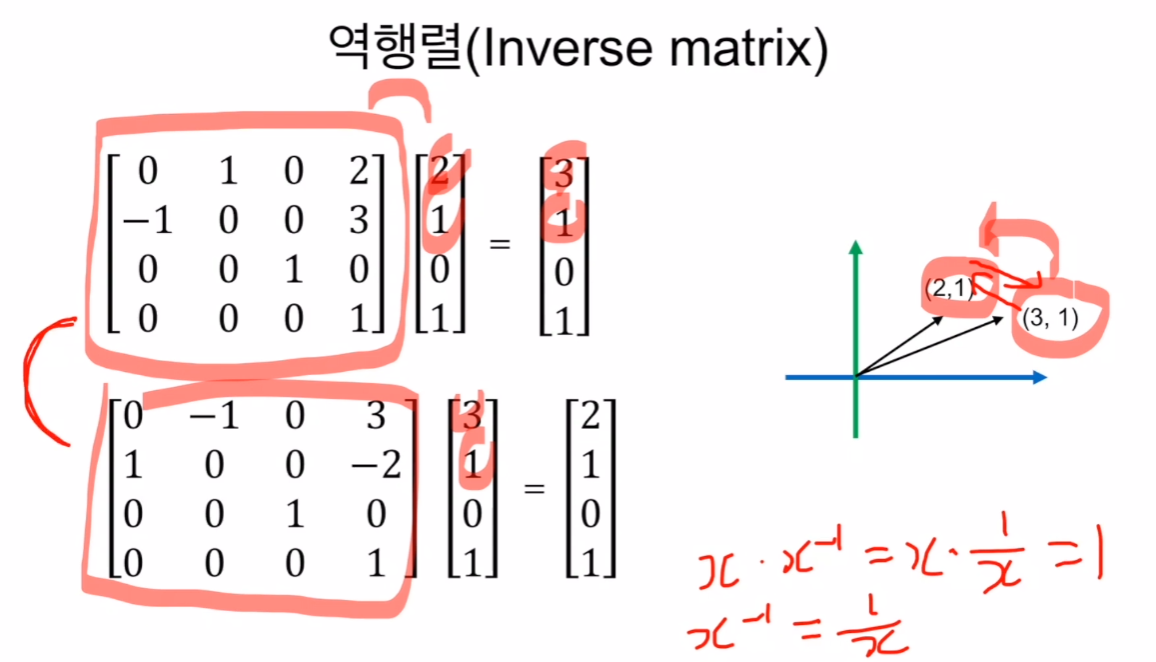
2,1에서 3,1을 가기위해 곱한 행렬과,
3,1에서 2,1에 가기위해 곱한 행렬
그 2개의 행렬을 서로의 역행렬이라고 부른다.
그 둘끼리 곱하면 단위행렬이 된다.
그 순서를 바꿔도 같다.
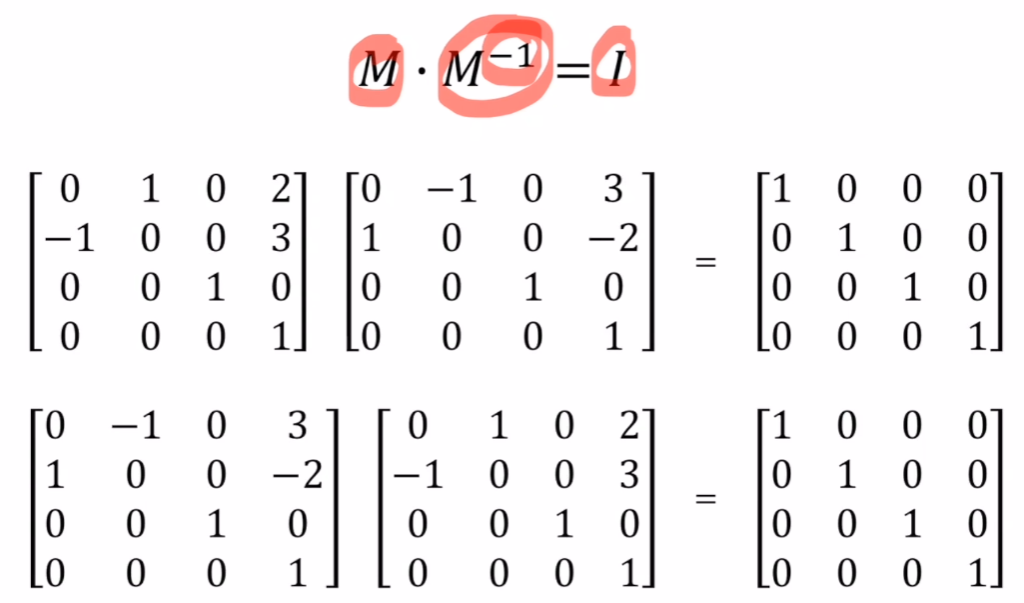
의미상으로는,
M이라는 행렬이 transform을 의미한다면,
M-1은 해당 transform을 원래대로 돌려놓는 반대의 transform을 의미한다.
좌표변환
투영의 종류에는 원근투영, 직교투영이 존재한다
perspective
원근투영 - 3D에서 주로 사용하고 원근법이 적용된다. 실제와 가깝다.
ortgigraogic
직교투영 - 2D에서 주로 사용하고 원근법이 배제된 채로 투영시킨다.
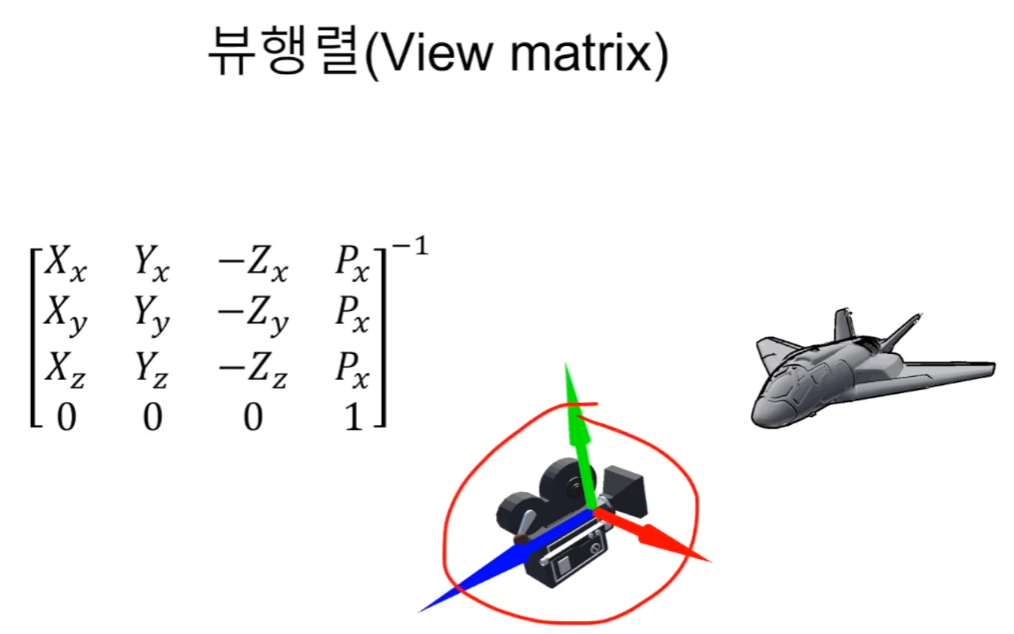
뷰공간의 행렬은 카메라의 transform의 역행렬이다
그 이유는 카메라를 기준으로 다른 오브젝트들이 상대적으로 변환되어야 한다.
카메라를 위로 올린다면,
상대적으로 다른 물체는 아래로 내려가는 형태가 될 것이다.
유니티 기준으로는 카메라가 -z 방향으로 행렬이 존재해야 한다.
z축이 카메라의 뒤쪽을 가리켜야한다고 한다.
원근 투영을 자세히 보면,
네모로부터 시작해서 네모로 끝난다.

카메라기준으로 네모난 단면이 2개가 존재하고,
가까운 작은 네모를 near를 줄여서 n으로 표현하고,
먼 것을 far을 줄여서 f로 표기하곤 한다.
ltn은, left, top, 뭐 이런 느낌이고,
n은 특정 상수인데, -라고 음수가 붙은 이유는,
z가 음의 방향이라 그렇다고 한다.
왼손좌표계랑 다른가?
그래서 카메라로부터 생긴 꼭다리 잘린 피라미드 속 공간을
NDC라는 정육면체공간으로 바꿔주는 것이 원근 투영 행렬이라고 한다.
NDC는 normalized 답게 좌표공간이 1기준으로 맞춰져 있다.
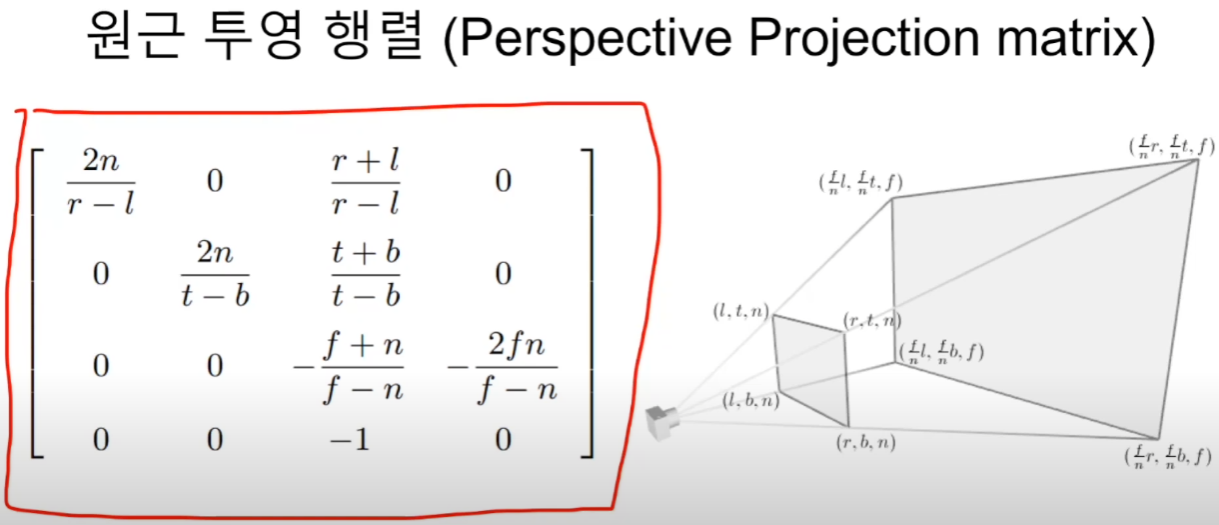
피라미드에서 NDC로 바꿔주는 행렬이다.
일단 스킵
행렬식

행렬 M에 대한 행렬식은 위의 3가지 방식으로 구현이 된다.
그래서 ad-bc라는 값이 무슨 의미가 있는가
이전에 벡터의 크기를 |V|이런 표시를 한다고 했다.
행렬식도 |M|과 같이 표시하고, 행렬을 통해 변화량의 크기를 나타낼 수 있다고 한다.
det M determinant가 행렬식이라는 의미이다.
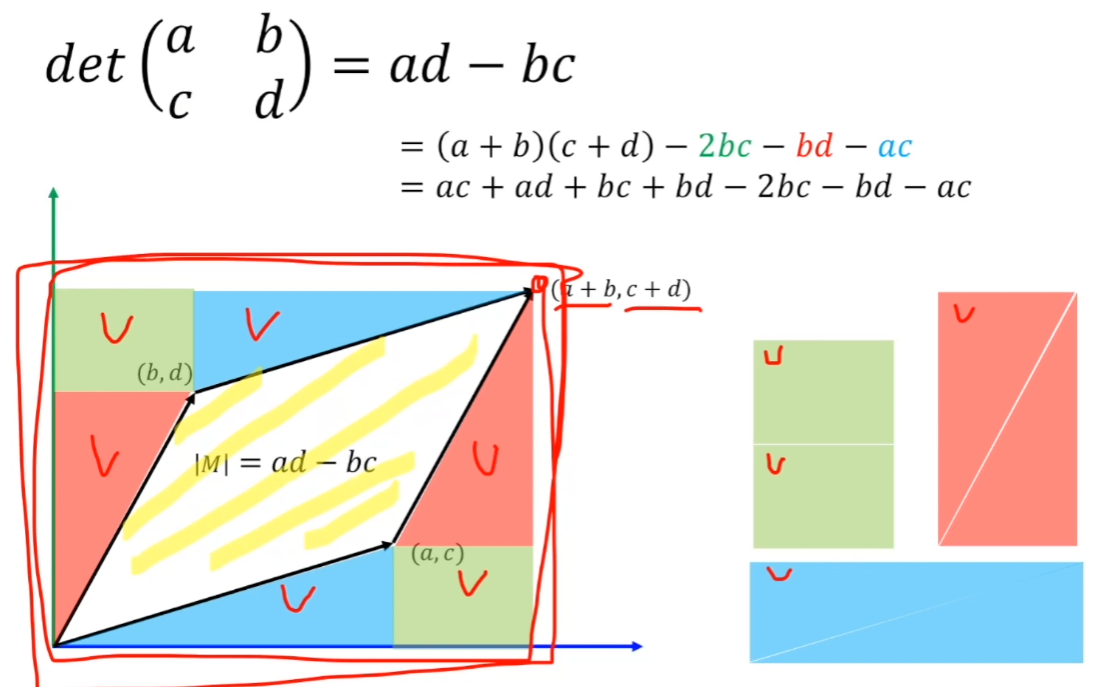
ac, bd라는 행렬로 본다면, 전체 직사각형에서 해당 마름모를 제외한
나머지를 계산하는데에 ad-bc라는 식이 유추되게 된다.
이는 열 행렬이기 떄문에 이렇고, 행기준 행렬은 같은 방식으로 하면 된다
그냥 똑같이 대각선곱하고 빼면 된다

예전에 구현해본 것들인데,
행기준 행렬인 2,1을 M을 곱하여 2,2가 되었는데,
얼마나 커지는지 계산하기 위해 |M|을 구한다면,
1x2 - 0x0 = 2가 된다.
즉 해당 벡터를 2배 스케일 했다는 것이다.
아래 회전에 대한 식은, 0 + 1 = 1으로,
회전만했지, 벡터 크기의 스케일연산은 없으므로, 1로 나온다.

3차원 벡터는 엄청나게 복잡하게 나오는데,
보면 나름의 규칙이 존재한다.
각 규칙에 따라 3가지 요소를 빼내고, (x - y + z) 식에 넣으면 된다
첫번째 변환식까지만 보면 된다.
첫번쨰 변환식에서 해당 aM에서 M을 |M|계산을 취하여 풀어주면 된다.
벡터의 외적
외적은 직교하는 뭔가가 나온다.
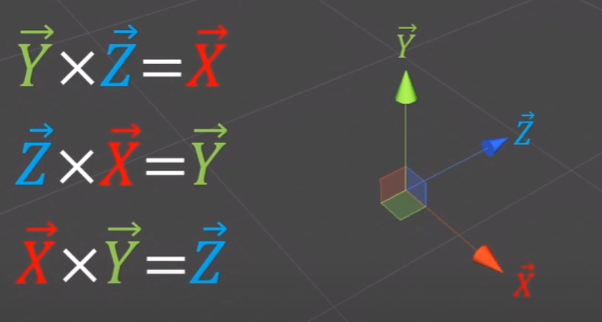
X라는 기호가 벡터의 외적을 의미한다.
벡터의 내적은 계산 순서가 바뀌어도 값이 같다.
내적을 이루는 요소는 같고 순서만 바뀌어서.
하지만 외적은 다르다.
순서가 바뀌면, 외적은 달라진다.
외적의 교환법칙은 성립하지 않는다.

이것도 외워야하는데,
위처럼 행기준 행렬처럼 만들고,
23 32 - 13 31 + 12 21을 하면 된다.
벡터 A,B의 외적은,
벡터 A와 벡터 B를 동시에 직교하는 벡터를 의미한다.
내적처럼 스칼라 값이 아닌, 벡터가 나오게 된다.
특징은 서로 직교하는 경우, 내적의 결과가 0이 나온다고 했다.
즉, A와 AXB를 내적하면 0, B와 AXB를 내적해도 0이 나올 것이다.
이를 식으로 만들고, 양변에 a1과 b1을 곱하고 이것저것하면
외적에 대한 식이 나오게 된다.
AXB인 외적을 |AXB|로 크기를 구한다면
해당 식은 |A||B|sinT이다.
내적은 |A||B|cosT이다.

A와 B의 외적의 크기는 A와 B가 이루는 평행사변형의 크기와 같다.
벡터의 내적은 한 벡터에(순서상관없음) 투영한(수직으로 내린) 다른 벡터값을 해당 기준이 된 벡터와 곱하는 것이다
그리고 벡터의 외적의 결과가 1인 단위벡터 나오기 위해서는,
A벡터와 B벡터끼리도 직교하고 있어야 하고,
해당 A벡터와 B벡터의 크기도 1이어야 한다는 특수한 상황이어야만 한다.
쉐이더에서 주로 내적을 많이 사용하지만,
노말맵을 다룰 때, 행렬을 다루는데, 외적으로 해당 행렬을 만들어야한다.
그때 해당 외적을 통한 벡터들이 정규화되지 않는다면, 공간이 왜곡되는 현상이 발생한다고 한다.