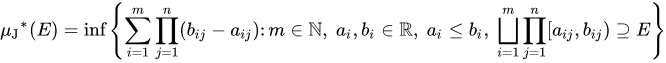[나만 보는 정리노트][르베그 적분 시리즈] 01. 조르당 측도

조르당 측도는 리만 적분을 정의하기 위해 필요한 측도이다.

특정 영역의 넓이를 측정하고 싶다고 할 때,
영역을 포함하는 단위 사각형들의 넓이의 합의 하한이 조르당 외측도이고,
영역에 포함되는 단위 사각형들의 넓이의 합의 상한이 조르당 내측도이다.

하한은 $\inf$으로 나타내며, 인파이멈(infimum)이라고 읽는다. 하한을 알기 위해선 하계에 대해 알아야 하는데, 집합 $S$의 하계는 $\{M\,|\,M\leq s\quad \forall s \in S\}$로 정의되며, 하계의 최댓값이 하한이다.

상한은 $\sup$으로 나타내며, 슈프리멈(supremum)이라고 읽는다. 상한은 마찬가지로 상계의 최솟값으로 정의된다. 집합 $S$의 상계는 $\{m\,|\,m\geq s\quad \forall s \in S\}$로 정의될 것이다.

$\quad$
상한과 하한이 최댓값, 최솟값 대신 쓰이는 이유는 $(0, 1)$같은 경우에 최댓값이나 최솟값은 없지만 상한과 하한은 각각 $0$과 $1$로 존재하기 때문이다.

조르당 외측도와 내측도는 이렇게 개념적으로 이해하면 된다. 수식은 쓰기 귀찮으니 위키백과 문서를 참고하는 게 좋다.

https://ko.wikipedia.org/wiki/%EC%A1%B0%EB%A5%B4%EB%8B%B9_%EC%B8%A1%EB%8F%84

유클리드 공간 $\R^n$ 위의 유계 집합 $E\subseteq \R^n$에서 조르당 외측도$(\mu_J^*)$와 조르당 내측도$(\mu _{J*})$가 서로 같을 때, 집합 $E$를 조르당 가측 집합이라고 한다.
즉 조르당 가측 집합 $E$에서 조르당 측도 $\mu_J(E)=\mu_J^*(E)=\mu_{J*}(E)$이다.

유클리드 공간 $\R^n$은 실수 집합 $\R$의 곱집합이다. 즉 우리가 아는 $n$개의 축이 있는 $n$차원 개념이 유클리드 공간이다.

유계란 유한한 영역을 가지는 것을 의미한다. 상계를 가지고 있으면 위로 유계, 하계를 가지고 있으면 아래로 유계라고 표현하며, 둘 모두 가지고 있는 집합을 유계 집합이라고 부른다.

조르당 측도는 유한 가법성이 성립한다. 어떤 함수 $f(x)$가 $f(a+b)=f(a)+f(b)$를 만족할 때 $f(x)$에서 가법성이 성립한다고 한다. 조르당 측도에서 유한 가법성이 성립한다는 것은 유한 개의 집합 $S_1, S_2, \cdots, S_n$ 에 대해서 $\mu_J(\displaystyle\bigcup_{i=1}^{n}{S_i})=\sum_{i=1}^{n}{\mu_J(S_i)}$가 성립한다는 것이다.

조르당 측도는 가산무한집합에 대해서는 가법성이 성립하지 않기 때문에, 가산 가법성이 성립하는 새로운 측도인 르베그 측도가 발명되게 된다.