
🧭 DFS (Depth-First Search) - 깊이 우선 탐색 완전 정리
✅ DFS란?
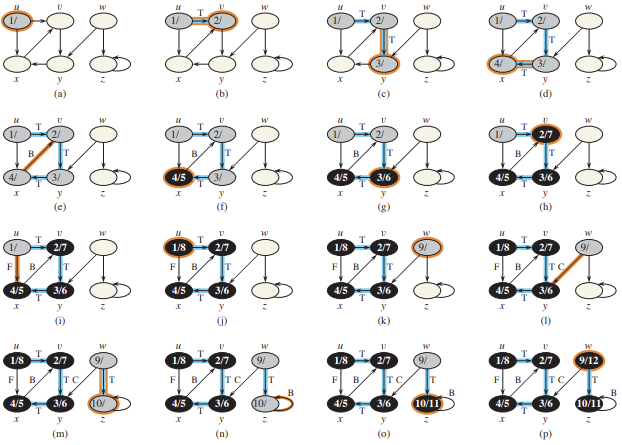
DFS(Depth-First Search, 깊이 우선 탐색)는 한 방향으로 가능한 한 깊게 탐색하고,
더 이상 갈 곳이 없으면 되돌아와 다른 경로를 탐색하는 알고리즘이다.
- 시작 노드를 방문하고, 방문 처리를 한다.
- 인접한 정점들 중 아직 방문하지 않은 노드를 재귀적으로 계속 방문한다.
- 더 이상 갈 곳이 없으면 한 단계 이전으로 되돌아간다 (backtracking)
→ 스택 구조로 동작하거나, 재귀 호출을 통해 자연스럽게 스택처럼 구현할 수 있다.
탐색의 흐름이 스택 구조를 따르며, 재귀 호출로 자연스럽게 구현할 수 있다.

✅ DFS는 어디에 쓰이나?
DFS는 다음 두 가지 경우에 사용된다.
| 대상 | 설명 | 방문 방식 |
|---|---|---|
| 트리(Tree) | 루트가 있고 사이클이 없는 구조 | 방문 순서로 전위 / 중위 / 후위 순회로 구분됨 |
| 그래프(Graph) | 일반적인 방향/무방향 구조 | 방문 배열이 필수, 경로가 여러 갈래일 수 있음 |
📌 DFS in Tree - 트리에서의 DFS
✅ DFS = 순회 (Traversal)
트리에서는 DFS 탐색이 곧 전위 / 중위 / 후위 순회로 나뉘며,
방문 시점(루트를 언제 출력하느냐)에 따라 구분된다.
| 순회 방식 | 순서 | 예시 활용 |
|---|---|---|
| 전위 순회 | 루트 → 왼쪽 → 오른쪽 | 트리 직렬화, 구조 출력 |
| 중위 순회 | 왼쪽 → 루트 → 오른쪽 | BST 정렬 결과 |
| 후위 순회 | 왼쪽 → 오른쪽 → 루트 | 트리 삭제, DP, 백트래킹 |
✅ 예시 트리
A
/ \
B C
/ \
D E
🔹 전위 순회 (Preorder) : A → B → D → E → C
🔹 중위 순회 (Inorder) : D → B → E → A → C
🔹 후위 순회 (Postorder) : D → E → B → C → A✅ 재귀 구현
class Node:
def __init__(self, key):
self.key = key
self.left = None
self.right = None
# 전위 순회
def preorder(node):
if node:
print(node.key, end=' ')
preorder(node.left)
preorder(node.right)
# 중위 순회
def inorder(node):
if node:
inorder(node.left)
print(node.key, end=' ')
inorder(node.right)
# 후위 순회
def postorder(node):
if node:
postorder(node.left)
postorder(node.right)
print(node.key, end=' ')
# 예시 트리 구성
root = Node('A')
root.left = Node('B')
root.right = Node('C')
root.left.left = Node('D')
root.left.right = Node('E')
preorder(root) # A B D E C
inorder(root) # D B E A C
postorder(root) # D E B C A✅ 반복 구현
전위 순회는 스택을 이용해 반복적으로도 구현 가능하다.
중위/후위 반복 구현은 복잡도가 조금 더 높기 때문에 보통 재귀가 선호된다.
def preorder_iterative(root):
if not root:
return
stack = [root]
while stack:
node = stack.pop()
print(node.key, end=' ')
if node.right:
stack.append(node.right)
if node.left:
stack.append(node.left)📌 DFS in Graph - 그래프에서의 DFS
✅ 핵심 개념
그래프에서는 DFS가 모든 연결된 노드를 깊게 탐색 하기 위해 사용된다.
하지만 사이클이 존재할 수 있기 때문에 반드시 방문 체크 배열이 필요 하다.
✅ 인접 리스트 + 재귀 구현
def dfs(graph, v, visited):
visited[v] = True
print(v, end=' ') # 방문 시 출력
for neighbor in graph[v]:
if not visited[neighbor]:
dfs(graph, neighbor, visited)
# 예시 그래프 (0부터 시작하는 무방향 그래프)
graph = {
0: [1, 2],
1: [0, 3, 4],
2: [0],
3: [1],
4: [1]
}
visited = [False] * 5
dfs(graph, 0, visited) # 출력: 0 1 3 4 2✅ 스택 구현
def dfs_stack(graph, start):
visited = set()
stack = [start]
while stack:
node = stack.pop()
if node not in visited:
print(node, end=' ')
visited.add(node)
# 인접 노드를 역순으로 넣어야 왼쪽부터 방문됨
for neighbor in reversed(graph[node]):
if neighbor not in visited:
stack.append(neighbor)
# 같은 그래프 사용
dfs_stack(graph, 0) # 출력: 0 1 3 4 2🔄 트리 DFS vs 그래프 DFS
| 항목 | 트리 DFS | 그래프 DFS |
|---|---|---|
| 구조 | 루트가 있고 사이클 없음 | 방향/무방향 가능, 사이클 존재 가능 |
| 순회 방식 | 전위 / 중위 / 후위로 명확히 구분 | 방문 순서는 경로에 따라 달라짐 |
| 방문 체크 | ❌ 필요 없음 | ✅ 반드시 필요함 |
| 구현 복잡도 | 단순 (재귀 구현이 쉬움) | 방문 배열, 분기 경로 고려 필요 |
| 대표 용도 | 트리 직렬화, DP, 순회 출력 | 경로 탐색, 사이클 탐지, 연결 요소 분석 |
| 재귀 깊이 | 트리의 높이만큼 제한적 | 연결 구조에 따라 깊어질 수 있음 |
| 출력 일관성 | 루트 기준 항상 동일 | 시작 노드, 연결 상태에 따라 유동적 |
| 시간 복잡도 | O(N) (노드 수) | (인접 리스트): O(V + E) |
- 트리 DFS는 구조가 단순하고 사이클이 없어서 구현이 간단하며, 순회 방식(전/중/후위)이 명확히 구분된다.
- 그래프 DFS는 구조가 복잡하고 분기/사이클이 존재할 수 있으므로 방문 처리가 필수이며, 경로에 따라 결과가 달라진다.
✅ DFS 응용
| 분야 | 활용 예시 |
|---|---|
| 트리 | 구조 출력, 순회, 서브트리 DP, 백트래킹 |
| 그래프 | 경로 탐색, 사이클 검출, 연결 요소, 위상 정렬 |
| 퍼즐/게임 | 조합 탐색, 미로 찾기 |
| 기타 | 재귀 기반 로직 구현, 구조 분석 |
🌐 DFS vs BFS
| 항목 | DFS | BFS |
|---|---|---|
| 방식 | 깊이 우선 | 너비 우선 |
| 자료구조 | 스택 (or 재귀) | 큐 |
| 경로 우선순위 | 한 방향으로 깊게 | 가까운 정점부터 |
| 구현 난이도 | 상대적으로 간단 | 방문 처리 주의 필요 |
| 응용 | 경로 탐색, 백트래킹 | 최단 경로, 레벨 탐색 |
🌐 DFS vs BFS 시간복잡도 - 자료구조 & 표현 방식
| 탐색 | 자료구조 | 표현 방식 | 시간 복잡도 | 설명 |
|---|---|---|---|---|
| DFS | 트리 | 인접 리스트 | O(N) | 트리는 간선 N-1개, 각 노드 1회 방문 |
| DFS | 트리 | 인접 행렬 | O(N²) | 모든 노드마다 N개 확인 (불필요한 검사 포함) |
| DFS | 그래프 | 인접 리스트 | O(V + E) | 각 정점 + 인접한 간선만 순회 |
| DFS | 그래프 | 인접 행렬 | O(V²) | 정점마다 전체 정점 검사 (간선 유무 확인) |
| BFS | 트리 | 인접 리스트 | O(N) | 트리는 레벨 순회여도 정점과 간선 수가 제한됨 |
| BFS | 트리 | 인접 행렬 | O(N²) | 자식 찾을 때 매번 N개 검사 |
| BFS | 그래프 | 인접 리스트 | O(V + E) | 큐로 정점과 간선 모두 한 번씩 확인 |
| BFS | 그래프 | 인접 행렬 | O(V²) | 각 정점마다 전체 정점 확인 필요 |
🎯 마무리 요약
- DFS는 트리와 그래프 모두에서 사용되는 기본 탐색 알고리즘이다.
- 트리에서는 전위 / 중위 / 후위 순회로 DFS가 구분되며, 방문 배열이 필요 없다.
- 그래프에서는 방문 배열이 반드시 필요하며, 경로가 여러 갈래로 뻗어나갈 수 있다.
- DFS는 백트래킹, 경로 탐색, 위상 정렬 등 다양한 알고리즘의 기반이 된다.
