🌐 그래프(Graph) 기초 완벽 정리 - 구조, 표현, 방향성

---

✅ 그래프란?

그래프는 정점(Vertex)과 간선(Edge)으로 이루어진 자료구조로,
현실 세계의 복잡한 관계를 모델링하는 데 자주 사용된다.
예를 들어, 지도, SNS 관계, 컴퓨터 네트워크, 웹 페이지 링크 구조 등이 그래프로 표현된다.

---

✅ 기본 용어

용어	설명
정점(Vertex)	노드라고도 부르며, 하나의 개체를 의미
간선(Edge)	두 정점을 연결하는 선
아크(arc)	단방향 간선
방향 그래프	간선에 방향이 있는 그래프 (A → B)
무방향 그래프	간선에 방향이 없는 그래프 (A — B)
가중치(Weight)	간선에 부여된 비용 또는 거리
인접 정점	간선으로 직접 연결된 두 정점
인접 리스트	각 정점에 연결된 정점 목록으로 표현
인접 행렬	정점을 행과 열로 표현한 2차원 배열

---

✅ 그래프의 종류

그래프는 구조에 따라 다양한 기준으로 분류된다.
또한 알고리즘 관점에서 의미 있는 특수 그래프도 존재하며, 이는 이후 문제 풀이에서 자주 등장한다.

---

🟢 1. 구조적 분류 (기초 그래프 종류)

분류	설명
무방향 그래프	간선에 방향이 없는 그래프 (A — B)
방향 그래프	간선에 방향이 있는 그래프 (A → B)
가중치 그래프	간선에 거리나 비용이 존재하는 그래프
비가중치 그래프	모든 간선의 가중치가 동일 (보통 1)
연결 그래프	모든 정점 간에 경로가 존재하는 그래프
비연결 그래프	어떤 정점 쌍 간에 경로가 없는 그래프
순환 그래프 (Cyclic)	사이클이 존재하는 그래프
비순환 그래프 (Acyclic)	사이클이 존재하지 않는 그래프

---

🔵 2. 알고리즘적 특수 그래프

그래프	설명	주요 알고리즘
DAG (Directed Acyclic Graph)	방향 그래프이면서 사이클이 없음	위상 정렬, DP 최적화, 경로 그래프
MST 그래프 (Minimum Spanning Tree)	모든 정점을 최소 비용으로 연결한 트리 구조 (무방향 가중치 그래프에서)	크루스칼, 프림
트리(Tree)	사이클이 없는 연결 그래프, 사실상 DAG의 일종	DFS/BFS, LCA, DP on tree
완전 그래프 (Complete Graph)	모든 정점이 서로 직접 연결됨 (n(n-1)/2개의 간선)	조합적 분석, 그래프 밀도 계산
양방향 DAG	논리적으로는 방향 그래프지만 실질적으로는 트리처럼 동작하는 구조	위상 정렬, 백트래킹 최적화
이분 그래프 (Bipartite Graph)	정점을 두 그룹으로 나눌 수 있으며, 그룹 내 연결 없음	매칭 문제, 색칠 문제, 네트워크 플로우

여기에서 DAG는 위상 정렬(Topological Sort)의 대상이 된다.
사이클이 없기 때문에 선후 관계를 표현하는 데 적합하며,
컴파일러의 빌드 순서, 강의 수강 순서, 의존성 그래프 등 현실 문제에 자주 등장한다.

---

✅ 그래프 표현 방법

그래프는 컴퓨터 메모리에 다양한 방식으로 표현할 수 있으며,
대표적으로 인접 리스트(Adjacency List)와 인접 행렬(Adjacency Matrix)이 사용된다.
각 방식은 시간/공간 효율성과 구현 목적에 따라 선택해야 한다.

---

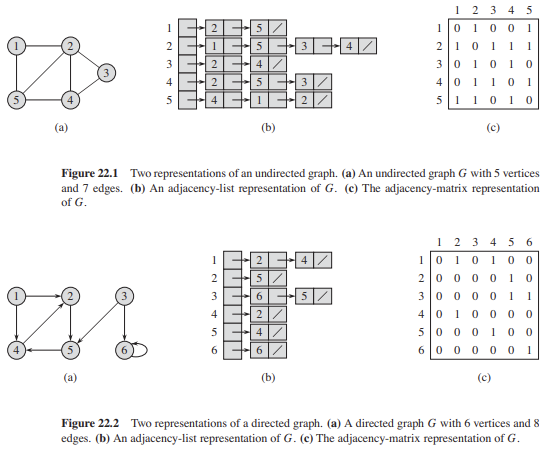
인접 리스트 (Adjacency List)

• 각 정점마다 연결된 정점들의 리스트를 저장하는 방식
• 연결 정보만 저장하므로 공간 효율성이 뛰어남

인접 행렬 (Adjacency Matrix)

• 그래프를 2차원 배열로 표현하는 방식
• 정점 간의 연결 여부를 배열의 값으로 표시 (1 or 0, 또는 가중치 값)

---

시간 복잡도 비교

연산	인접 리스트	인접 행렬
정점 간 연결 여부 확인	O(k) (k: 연결된 정점 수)	O(1)
모든 인접 정점 순회	O(k)	O(V)
간선 추가/삭제	O(1) 또는 O(k)	O(1)

공간 복잡도 비교

표현 방식	공간 복잡도
인접 리스트	O(V + E)
인접 행렬	O(V²)

정리

기준	인접 리스트	인접 행렬
그래프 밀도	희소 그래프에 적합	밀집 그래프에 적합
공간 효율성	뛰어남	낮음
연결 여부 확인	느림 (O(k))	빠름 (O(1))
구현 복잡도	다소 복잡	단순

---

✅ 그래프를 트리와 비교하면?

항목	트리	그래프
순환	없음	가능함
간선 수	n - 1	제한 없음
계층 구조	존재	없음 (복잡한 연결 가능)
루트 존재	있음	없음 (아무 노드에서 시작 가능)
대표 탐색법	DFS, BFS, 순회 등	DFS, BFS, 최단경로, MST 등

---

✅ 파이썬에서 그래프 선언 팁

dict + list 조합** 으로 인접 리스트를 표현하는 게 가장 보편적
방향/무방향 여부에 따라 간선 양방향 추가 여부를 결정

from collections import defaultdict

graph = defaultdict(list)
# import 없이 graph = {i: [] for i in range(1, N + 1)} 로도 가능하다

# 무방향 그래프
graph[0].append(1)
graph[1].append(0)

# 방향 그래프
graph[2].append(3)  # 2 → 3

# 만약 key당 value가 여러 개인 형태의 인접리스트가 되었고, 작은 번호를 먼저 방문해야 한다면 써주자
for node in graph:
    graph[node].sort()

---

🎯 마무리 요약

• 그래프는 복잡한 관계 구조를 표현하는 핵심 자료구조다.
• 정점과 간선으로 구성되며, 방향/가중치 여부에 따라 다양한 형태를 가진다.
• 인접 리스트는 메모리 효율이 좋고, 알고리즘 적용이 쉽다.
• 트리보다 범용성이 높아, 이후 DFS, BFS, 다익스트라, 위상 정렬 등으로 확장된다.