[자료구조] AVL 트리

100·2025년 3월 28일

자료구조 & 알고리즘

목록 보기

3/20

⚖️ AVL 트리 완벽 정리 - 균형 잡힌 이진 탐색 트리

✅ AVL 트리란?

AVL 트리는 이진 탐색 트리(BST)의 일종으로, 모든 노드에 대해 왼쪽과 오른쪽 서브트리의 높이 차이가 1 이하가 되도록 유지하는 균형 이진 트리이다.
1959년에 Adelson-Velsky와 Landis가 처음 제안해서 이름이 붙었다.

BST는 데이터가 한쪽으로 편향되면 선형 구조가 되어 탐색 성능이 O(n)까지 떨어질 수 있는데,
AVL 트리는 자기 균형(Self-Balancing) 기능을 통해 항상 O(log n)의 탐색 성능을 유지한다.

✅ AVL 트리의 핵심 개념

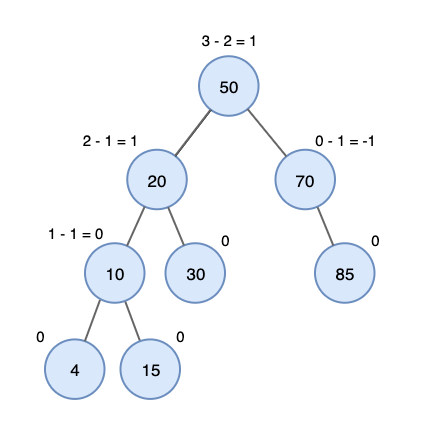
🔹 균형 인수(Balance Factor)

각 노드는 왼쪽 서브트리 높이 - 오른쪽 서브트리 높이 값을 가지며, 이를 균형 인수(Balance Factor)라고 한다.

Balance Factor = -1, 0, 1 → 균형 상태 유지
Balance Factor가 ±2 이상이 되면 불균형 → 회전 필요

🔄 회전(Rotation) 패턴

균형이 깨졌을 때, 구조를 회전시켜서 트리를 재구성한다.
불균형 발생 패턴은 총 4가지가 있다.

✅ LL 회전 (단순 오른쪽 회전)
- 왼쪽 자식의 왼쪽에서 삽입된 경우

    Before:                After:
        30                   20
       /                    /  \
      20         →         10   30
     /
    10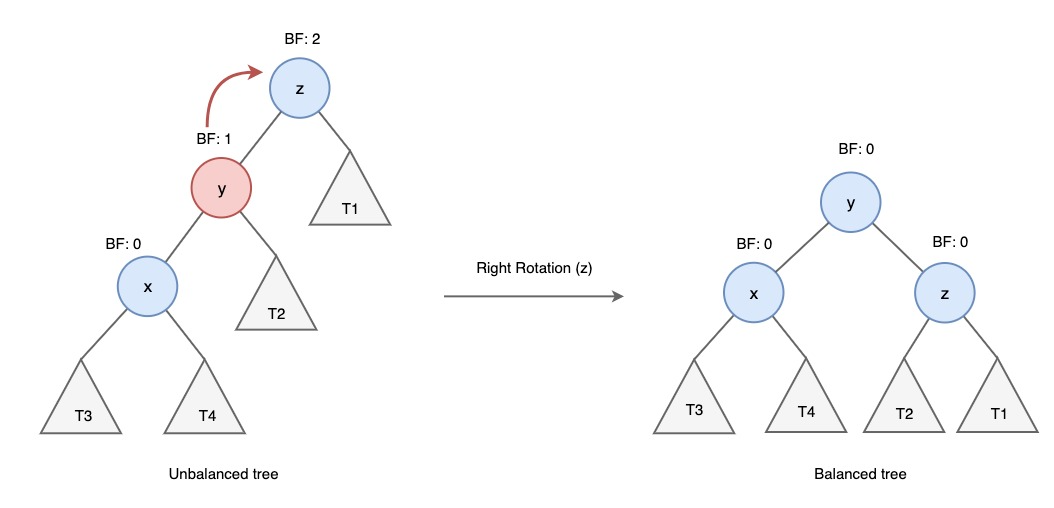

✅ RR 회전 (단순 왼쪽 회전)
- 오른쪽 자식의 오른쪽에서 삽입된 경우

    Before:                After:
      10                     20
        \                  /   \
         20     →         10    30
           \
            30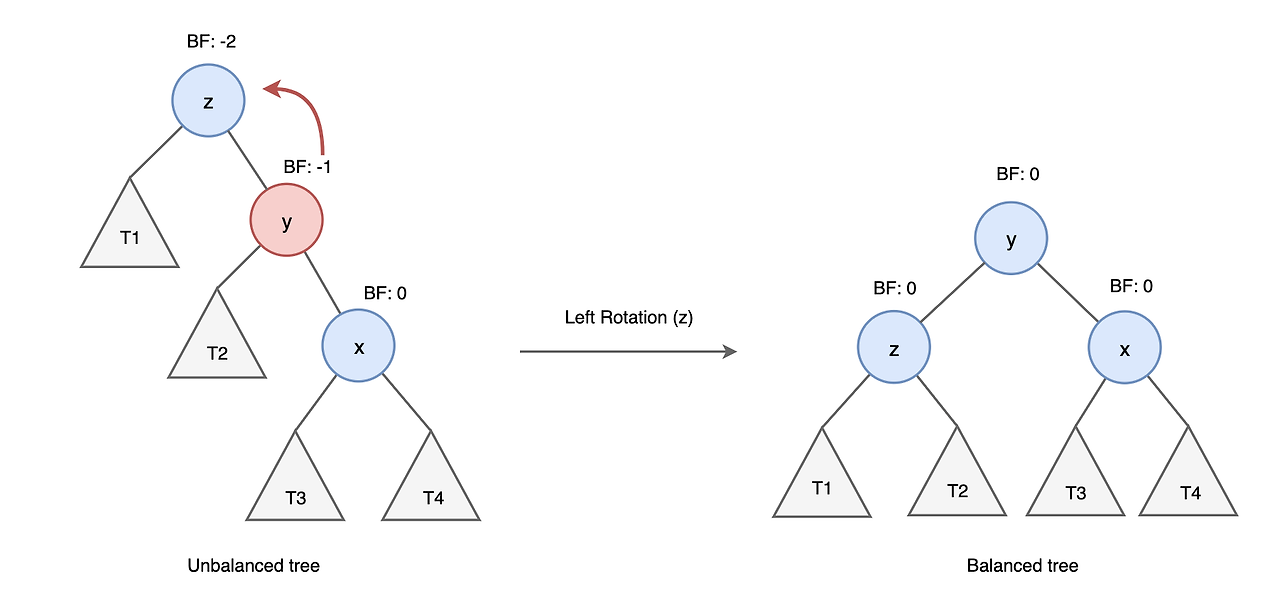

✅ LR 회전 (왼쪽-오른쪽 이중 회전)
- 왼쪽 자식의 오른쪽에서 삽입된 경우

    Before:                  Step 1 (Left Rotate):         Step 2 (Right Rotate):
        30                         30                              20
       /                          /                              /   \
      10             →          20               →            10      30
        \                      /
         20                 10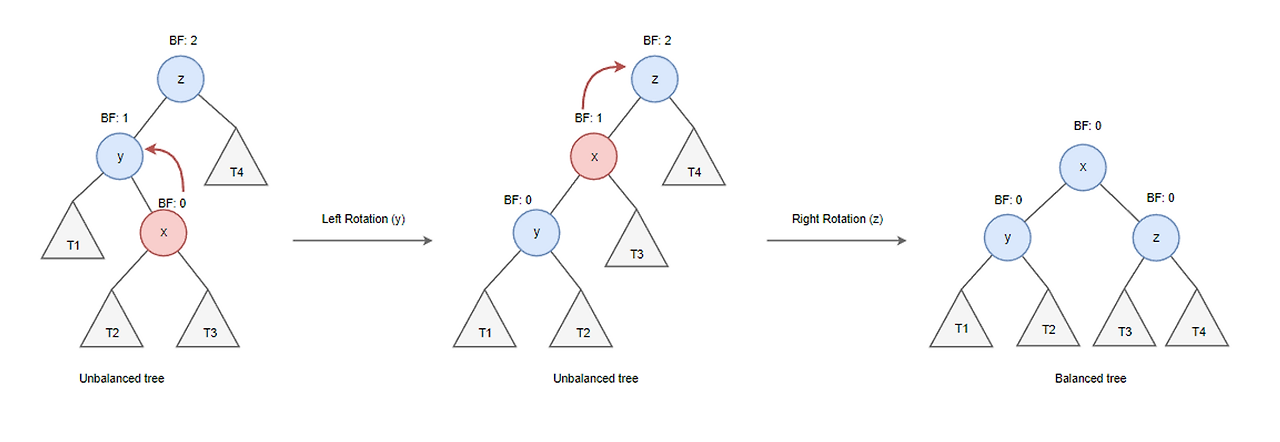

✅ RL 회전 (오른쪽-왼쪽 이중 회전)
- 오른쪽 자식의 왼쪽에서 삽입된 경우

    Before:                  Step 1 (Right Rotate):        Step 2 (Left Rotate):
      10                          10                             20
        \                           \                          /   \
         30            →            20            →         10       30
        /                              \
       20                              30

업로드중..

✅ 파이썬 구현 예제 (삽입만 포함)

class Node:
    def __init__(self, key):
        self.key = key
        self.left = None
        self.right = None
        self.height = 1  # 노드의 높이 정보

def get_height(node):
    return node.height if node else 0

def get_balance(node):
    return get_height(node.left) - get_height(node.right) if node else 0

def rotate_right(y):
    x = y.left
    T2 = x.right

    x.right = y
    y.left = T2

    y.height = 1 + max(get_height(y.left), get_height(y.right))
    x.height = 1 + max(get_height(x.left), get_height(x.right))

    return x

def rotate_left(x):
    y = x.right
    T2 = y.left

    y.left = x
    x.right = T2

    x.height = 1 + max(get_height(x.left), get_height(x.right))
    y.height = 1 + max(get_height(y.left), get_height(y.right))

    return y

def insert(node, key):
    if not node:
        return Node(key)

    if key < node.key:
        node.left = insert(node.left, key)
    elif key > node.key:
        node.right = insert(node.right, key)
    else:
        return node  # 중복은 허용하지 않음

    node.height = 1 + max(get_height(node.left), get_height(node.right))
    balance = get_balance(node)

    # LL
    if balance > 1 and key < node.left.key:
        return rotate_right(node)
    # RR
    if balance < -1 and key > node.right.key:
        return rotate_left(node)
    # LR
    if balance > 1 and key > node.left.key:
        node.left = rotate_left(node.left)
        return rotate_right(node)
    # RL
    if balance < -1 and key < node.right.key:
        node.right = rotate_right(node.right)
        return rotate_left(node)

    return node

# 중위 순회
def inorder(node):
    if node:
        inorder(node.left)
        print(node.key, end=' ')
        inorder(node.right)

# 테스트
root = None
for key in [30, 20, 10, 25, 40, 50, 5]:
    root = insert(root, key)

print("Inorder Traversal (오름차순 출력):")
inorder(root)