
🟥⬛ Red-Black Tree 완벽 정리 - 느슨한 균형, 강력한 성능
✅ Red-Black Tree란?
Red-Black Tree(레드블랙 트리)는 이진 탐색 트리(BST)의 일종으로, 삽입과 삭제 연산 시 트리의 균형을 유지하기 위해 노드에 색상 속성을 부여한 구조이다.
AVL 트리보다 리밸런싱이 느슨하지만, 삽입/삭제 성능이 더 우수해 실전에서 더 자주 사용된다.
대표적인 예로 Java의 TreeMap, C++ STL의 map, 리눅스 커널의 스케줄링 큐 등에서 사용된다.
✅ 핵심 속성 5가지
Red-Black Tree는 다음 다섯 가지 규칙을 항상 만족해야 한다.
- 모든 노드는 빨강 또는 검정이다.
- 루트 노드는 항상 검정이다.
- 모든 리프(NIL) 노드는 검정이다.
- 빨강 노드의 자식은 항상 검정이다.
- 즉, 빨강 노드가 연속으로 등장할 수 없다.
- 어떤 노드에서 리프 노드까지 가는 모든 경로에는 같은 수의 검정 노드가 존재한다.
이러한 규칙들을 통해 트리의 높이를 제한하여 O(log n) 탐색 성능을 보장한다.
✅ 왜 필요한가?
- AVL 트리는 삽입/삭제마다 빈번하게 회전이 발생한다.
- Red-Black Tree는 균형이 다소 깨지더라도 트리 높이가 log n 내에서 유지되도록 조정한다.
- 그 결과, 삽입/삭제가 자주 일어나는 환경에서 뛰어난 성능을 보장한다.
🔁 삽입 시 균형 유지 방식
Red-Black Tree에서 새로운 노드는 항상 빨강(Red)으로 삽입된다.
이후 부모와 삼촌 노드의 색상을 확인하고, 3가지 케이스에 따라 처리한다.
🔹 Case 1: 부모와 삼촌이 모두 빨강
- 부모와 삼촌을 검정으로 바꾸고, 할아버지를 빨강으로 바꾼 후 루트까지 반복
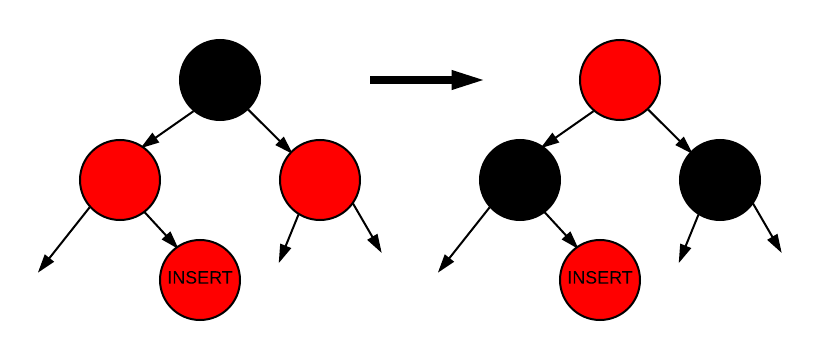
🔹 Case 2: 부모는 빨강, 삼촌은 검정, 현재 노드가 부모의 "반대 방향" 자식
- 부모 방향으로 회전하여 Case 3으로 변형
- Red-Black Tree 규칙상, 리프 노드는 모두 검정으로 간주되기 때문에, 삼촌이 없다는 건 검정 삼촌이 있는 것과 같은 의미
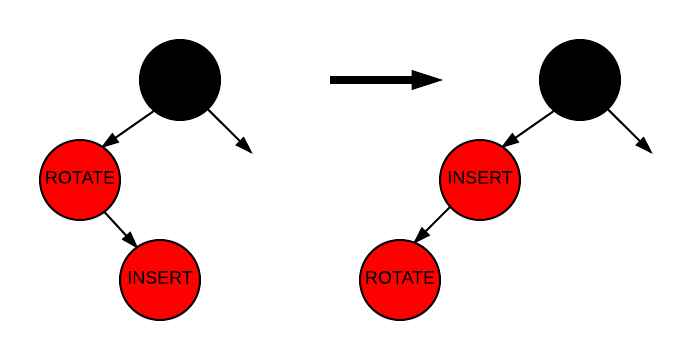
🔹 Case 3: 부모는 빨강, 삼촌은 검정, 현재 노드가 부모의 "일치 방향" 자식
- 할아버지 노드 기준으로 반대 방향으로 회전
- 부모와 할아버지의 색을 서로 바꾼다
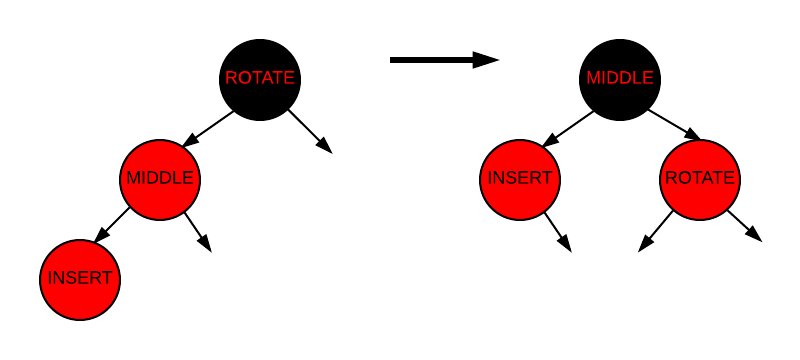
🔁 삭제 시 균형 유지 방식
Red-Black Tree에서 삭제는 BST처럼 노드를 제거한 뒤, 트리의 균형과 색상 규칙을 복구하는 과정이 추가된다.
특히 검정 노드를 삭제하면 "이중검정(Double Black)" 상태가 발생할 수 있으며, 이를 처리하기 위해 색상 변경과 회전이 사용된다.
복구는 형제(sibling) 노드의 색상과 자식 노드의 상태에 따라 다음 네 가지 케이스 중 하나로 분기된다.
-
형제가 RED
→ 부모와 색 교환 후 회전 → BLACK 형제 케이스로 전환 -
형제가 BLACK + 자식들이 모두 BLACK
→ 형제를 RED로 만들고 이중검정을 부모로 전파 -
형제가 BLACK + 가까운 자식만 RED
→ 형제와 자식 색 교환 + 형제 기준 회전 → Case 4로 전환 -
형제가 BLACK + 먼 자식이 RED
→ 부모와 색 교환 후 부모 기준 회전 → 이중검정 제거
Red-Black Tree 삭제는 구현이 복잡하지만, 이러한 규칙을 따라가면 항상 균형이 유지되며 O(log n) 성능을 보장한다.
✅ 시간 복잡도
- 탐색, 삽입, 삭제: O(log n)
- 트리 높이가 최대 2 * log(n)이므로 성능이 안정적으로 유지된다.
✅ 파이썬 구현 라이브러리
Red-Black Tree는 구현이 복잡하므로, 보통 직접 구현하지 않고 라이브러리를 활용한다.
rbtree(외부 모듈)bintrees모듈의RBTree- C++ STL:
map,set - Java:
TreeMap,TreeSet
🎯 마무리 요약
- Red-Black Tree는 색상 속성을 이용해 트리의 균형을 느슨하게 유지하는 이진 탐색 트리다.
- AVL보다 삽입/삭제에 효율적이며, 실제 시스템에서 널리 쓰인다.
- 모든 노드가 빨강 또는 검정이라는 특성과 5가지 규칙을 통해 높이를 제한하고 O(log n) 성능을 보장한다.
- 회전과 색상 변경을 적절히 조합하여 균형을 복구한다.
- 복잡한 구현보다는 원리를 이해하고, 실전에서는 라이브러리를 사용하는 것이 일반적이다.
