---

Box Plot

박스 플롯을 이용하면 데이터들의 중앙값과 이상치들을 빠르게 확인할 수 있다.
그럼 이러한 박스 플롯을 그리기 위한 개념들과 방법을 살펴보자.

이상치

이상치란 데이터들의 분포를 확인하였을 때, 일반적인 범위 내에서 벗어나, 평균과 같이 통계처리를 할 때 결과를 왜곡시킬 수 있는 값을 의미한다.

사분위수

사분위수는 데이터를 크기에 따라 4등분을 했다고 생각하면 된다.
이때, 4등분을 하면 그 나누어진 데이터 범위들의 경계는 3 곳이 될 것이다.
따라서 사분위수는 제 1 사분위수 (Q1), 제 2 사분위수 (Q2), 제 3 사분위수(Q3)로 3개가 된다.

👉 사분위수를 구하는 방법

1. 데이터들의 중앙값을 구한다. => Q2
2. Q2를 기준으로 왼쪽 데이터들만 고려할 때, 중앙값을 구한다. => Q1
3. Q2를 기준으로 오른쪽 데이터들만 고려할 때, 중앙값을 구한다. => Q3

다섯 숫자 요약

다섯 숫자 요약 (Five number summary)은 위의 사분위수들에 최소값과 최대값을 추가하여 표현하는 것이다.

[min, Q1, Q2, Q3, max]

Box Plot 그리는 법

1. 데이터들의 사분위수를 구한다.

2. Q1과 Q3을 상자로 연결한 후, Q2, 즉 중앙값의 위치에 선을 그어 표시한다.

3. Q3 - Q1을 계산하여 Q1과 Q3의 바깥쪽(각각 왼쪽, 오른쪽)으로 '1.5 (Q3 - Q1) 크기의 범위 내의 인접값'을 실선으로 연결하여 표시한다.

   1.5 (Q3 - Q1) 크기의 범위 내의 인접값? 데이터 값들 중 Q1 - 1.5 (Q3 - Q1) 와 가장 비슷한 값 / Q3 - 1.5 (Q3 - Q1) 와 가장 비슷한 값

   만약 이 값들이 데이터들의 최소, 최대값을 벗어나면 최소값과 최대값으로 라인을 표시한다.

4. 3번에서 표시한 라인을 벗어나는 데이터들을 동그라미로 표시한다. 이때 동그라미들을 극단값이라고 본다.

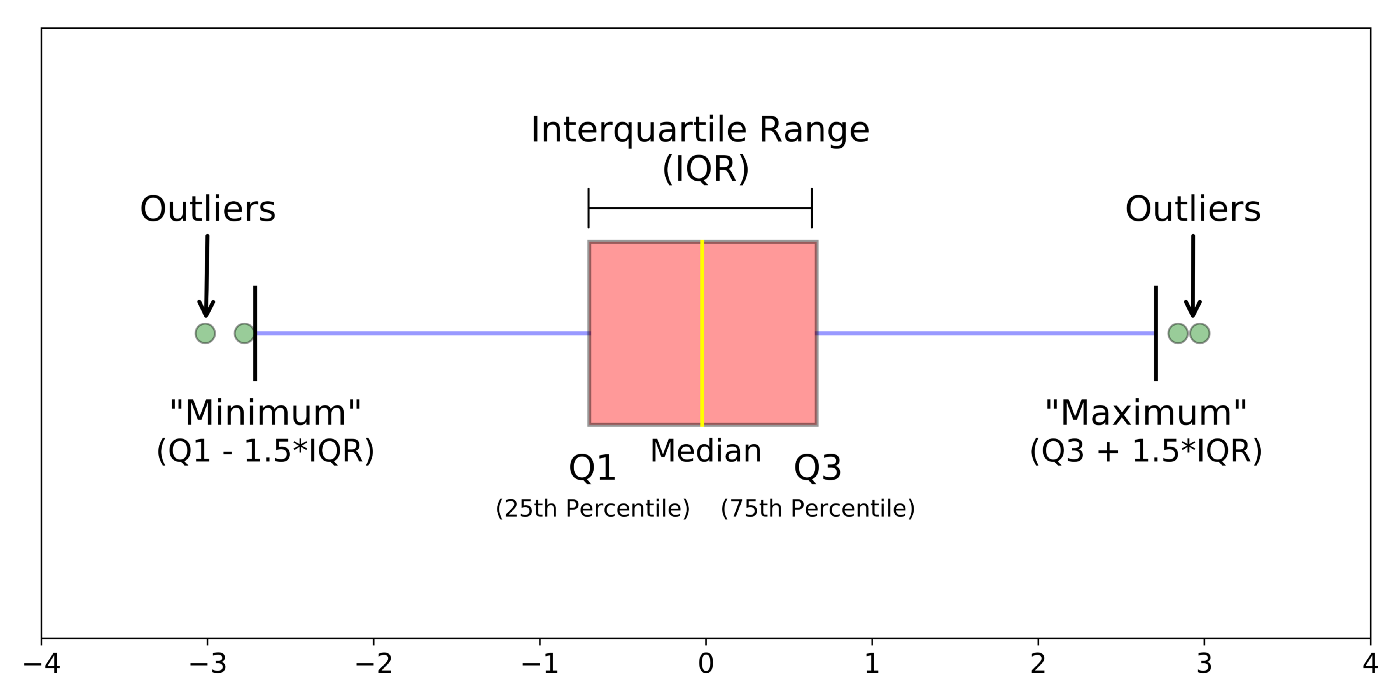
참고

https://towardsdatascience.com/understanding-boxplots-5e2df7bcbd51