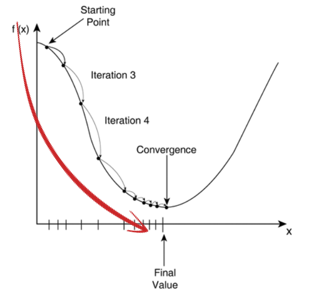
경사하강법이란?

• 경사 ⇒ 기울기
• 하강법 ⇒ 내려가는 방법
• 경사하강법 ⇒ 기울기를 따라 내려가는 방법

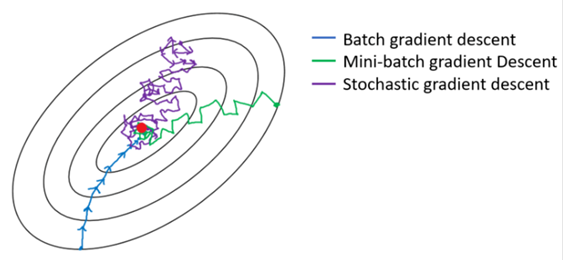
배치 경사하강법(Batch Gradient Descent)?

모든 학습 데이터를 사용하여 비용함수의 기울기를 계산한다. 일반적인 경사하강법은 이 배치 경사하강법을 의미한다. 전체 데이터를 사용하기 때문에 안정적이지만, 효율적이지 않다.

확률적 경사하강법(Stochastic Gradient Descent; SGD)?

하나의 샘플을 랜덤하게 골라 해당 데이터의 기울기를 따라 조금 내려간다. 이렇게 하나의 샘플씩 랜덤하게 선택하여 경사하강법을 취하는 것이 확률적 경사하강법이다. 만족할만한 최소값 위치에 도달할 때까지 계속 이를 반복적으로 시행한다.

그러나 이 방법은 랜덤한 하나의 샘플의 기울기를 기반으로 업데이트 되므로 잘못된 곳으로 업데이트가 될 수 있다.

미니배치 경사하강법(Minibatch Gradient Descent; Mini batch SGD)?

하나의 데이터가 아닌 여러개의 샘플을 랜덤으로 선택하여 그 데이터들의 비용함수의 기울기를 계산한다. SGD 보다 안정적이면서, BGD보다 효율적이므로 일반적으로 사용되는 기법이다.

Q. 미분계수가 0인 지점을 찾는 방식이 아닌 gradient descent를 이용해 함수의 최소값을 찾는 이유?

실제 미분계수를 계산하는 과정을 컴퓨터로 구현하는 것에 비해 gradient descent는 컴퓨터로 비교적 쉽게 구현할 수 있다. 데이터 양이 매우 큰 경우 한번에 모든 데이터에 대한 기울기를 구하는 것보다, 경사하강법과 같은 iterative한 방법을 통해 해를 구하는 것이 계산량 측면에서 더 효율적이다.