사전 수학 개념들

• 기저?

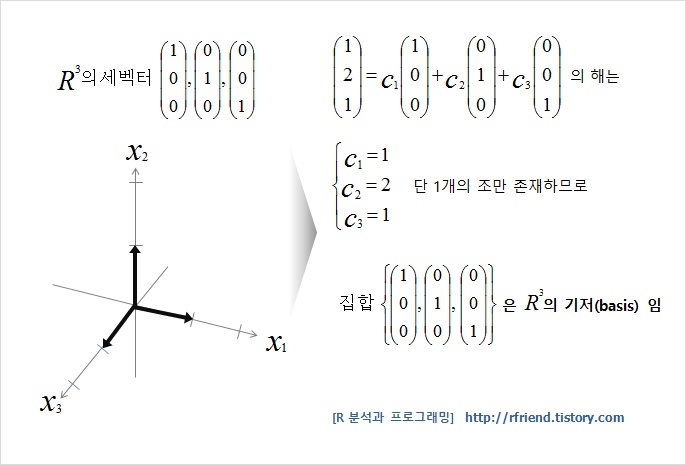
  백터공간 V에 대하여 임의의 벡터집합 S가

  ① 서로 1차 독립이면서

  ② 벡터공간 V를 생성하면

  S는 V의 기저이다.

  
  

  즉, 기저라 함은 특정 벡터 공간을 선형 생성하는 선형 독립인 벡터들로, S가 N 차원의 기저이면 N개의 벡터로 이루어져 있다.

  이때 기저의 크기는 일반적으로 길이가 1인 단위벡터로 표시한다. (크기보다는 방향이 중요하기 때문이다.)

• 고유값, 고유벡터

  행렬 A에 대해 다음 식을 만족한다고 가정하자.

  $Ax = λx$

  이때, λ는 고유값으로 스칼라라고도 한다.

  또한 이때 x를 고유벡터라고 한다.

  
  

  위 식을 기하하적인 입장에서 보면 고유값 λ는 변화되는 크기를 의미하며, x는 변화되는 방향을 의미한다.

  즉, 행렬 A에 대해 변환된 벡터 x가 λ배 만큼 확장 또는 축소가 된 것이다.

  
  

  선형대수학의 입장에서 고유값과 고유벡터 개념들을 다시 살펴보면 다음과 같다.

  고유값? det(λIn-A)=0 또는 det(A-λIn)=0 이 되게하는 λ이다.

  (이때 λIn는 λ1, λ2, … , λn을 주대각선으로 하는 대각행렬이다.)

  *det는 행렬식을 의미한다.

  고유벡터? (λIn-A)x=0 또는 (A-λIn)x=0 이 되는 x 전체의 집합이다. (단, x=0을 제외한다.)

물론 수학적으로 이를 풀이할 수 있어야 하지만, 기하학적인 입장에서 왜, 어떻게 이러한 과정들이 진행되는지 이해하는 것이 더 중요하다.

다시 기하학적인 관점에서 고유벡터와 고유값에 대해 생각해보자.

행렬 A의 고유벡터가 v1, v2이고 고유값을 λ1, λ2라고 할 때, 벡터 x에 행렬 A 변환을 가한다는 말은 v1, v2로 이루어진 고유벡터 공간에서 v1방향으로 λ1배, v2방향으로 λ2배 했다는 의미이다.

고유벡터는 변화되는 방향, 고유값은 변화되는 비율이라는 점을 기억하자.

고유값 분해(EVD)

N x N 크기의 정방행렬 A를 PDPT로 표현할 수 있다.

이때 P는 고유벡터 vi로 이루어진 행렬로 변화되는 방향을 의미한다.

이때 D는 고유값 λi로 이루어진 대각행렬로 변화되는 비율을 의미한다.

따라서 고유값 분해를 기하학적인 의미로 살펴보면 P 방향으로 돌리고, D만큼 확대 또는 축소를 한 후, 다시 원래 방향으로 복구하는 것을 의미한다.

SVD(Singular Value Decomposition)

정방행렬이 아닌, M x N 크기의 직사각행렬 A를 3단계로 나누어 분해할 수 있다. (m차원을 n차원으로 바꾸는 것이라고 볼 수 있다.)

A = U∑VT

이때 U는 A x AT로 m x m 직교 행렬이다.

이때 V는 AT x A 로 n x n 직교 행렬이다.

이때 ∑는 주대각 성분이 고유값 λ에 루트를 씌운 값인 m x n 직사각 대각행렬이다.

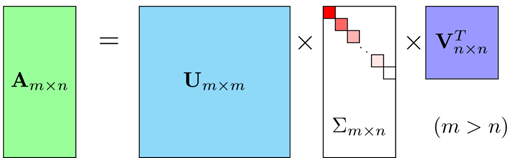
이미지 출처: https://www.pikpng.com/transpng/hxRRmbR/

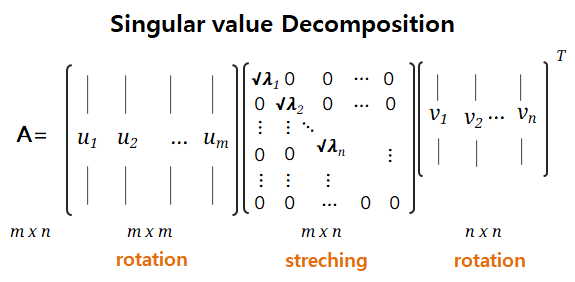
특이값 분해인 SVD는 고유값 분해 EVD와 기하학적인 해석으로는 의미가 비슷하다.

그러나 SVD는 A가 직사각 행렬일 때를 의미한다는 차이가 있다.

이로 인해, 고유값 분해에서는 고유벡터로 이루어진 행렬들이었던 P와 PT가, 특이값 분해에서는 U와 VT 를 정사각행렬로 변환해준 뒤 계산해진다는 것을 확인할 수 있다.

이렇게 제곱으로 계산이 된 고유벡터 값들에 대응되는 고유값을 구한 것이므로, 직사각 대각행렬 ∑에 주대각 성분으로 들어오는 고유값들에는 루트를 씌워주는 것이다.

SVD 종류

• full SVD

  

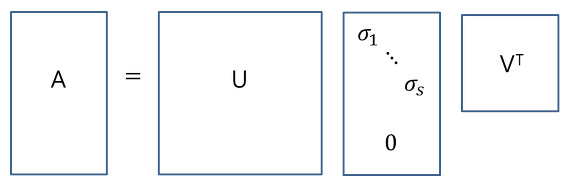
• thin SVD: Σ에서 마지막 주대각성분이 있던 값까지 해서 정방행렬로 바꾸어준 뒤, U에서도 이에 대응되는 열들을 지워준 것이다. 원본 복구가 가능하다.

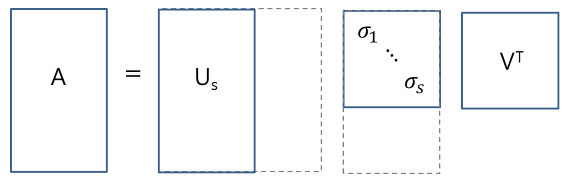
• compact SVD: 주대각 성분인 λ가 0인 것까지 다 지운다. 원본 복구가 가능하다.

  

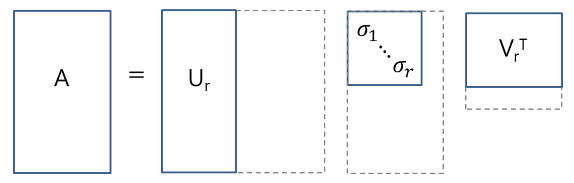
• truncated SVD: 주대각 성분인 λ가 0이 아닌 것까지 다 지운다. 원본 복구가 불가능하다.

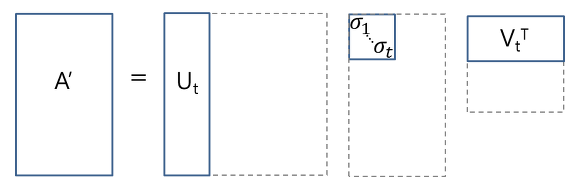
참고로 저주파는 왼쪽 상단에 해당되는 행렬로 중요한 정보들 밀집되어 있는 것이고, 고주파는 오른쪽 하단에 해당되는 행렬 디테일한 세부 정보들에 해당된다.

따라서 왼쪽 상단을 기준으로 데이터를 압축함으로써 정보들을 가능한 보존하는 것이다.

PCA(Princpal Component Analysis)

데이터 분포에 대한 주성분(Principal Component)을 찾는 것이다.

PCA의 목적은 최적의 feature 조합을 찾는 것으로, feature selection과 feature dimension reduction을 하기 위해 쓰인다.

• PCA 알고리즘 순서

1. 데이터의 평균으로 원점을 옮긴다.
2. 데이터의 공분산행렬, 고유값, 고유벡터를 구한다.
3. 고유벡터를 기저라고 가정하고 데이터를 보면, 가장 큰 분산을 관점으로 보게 된다.

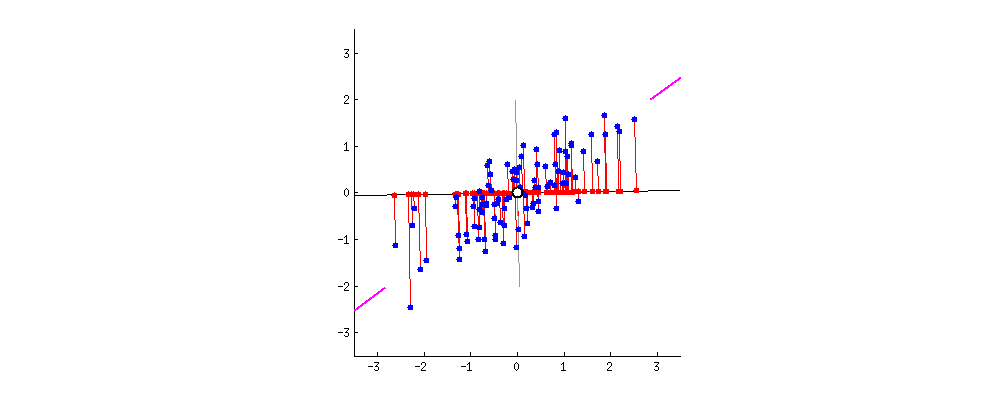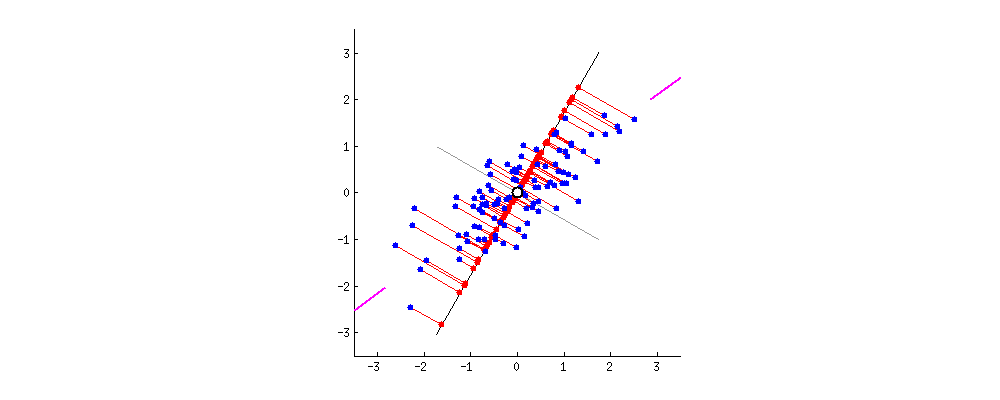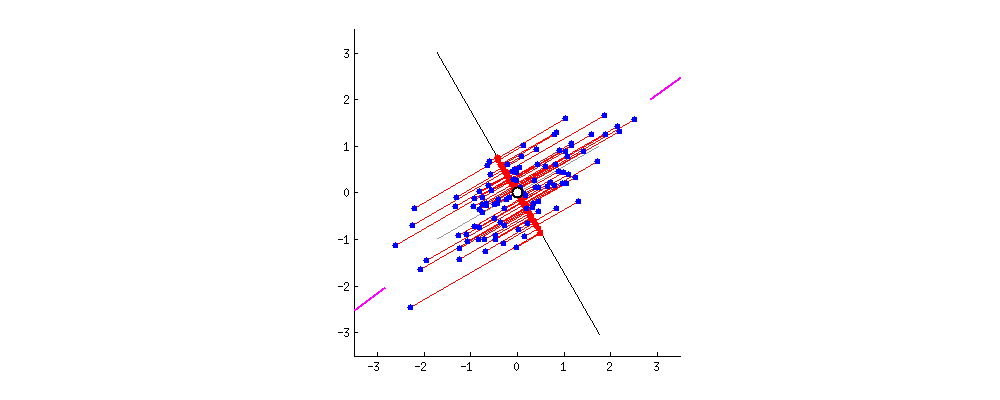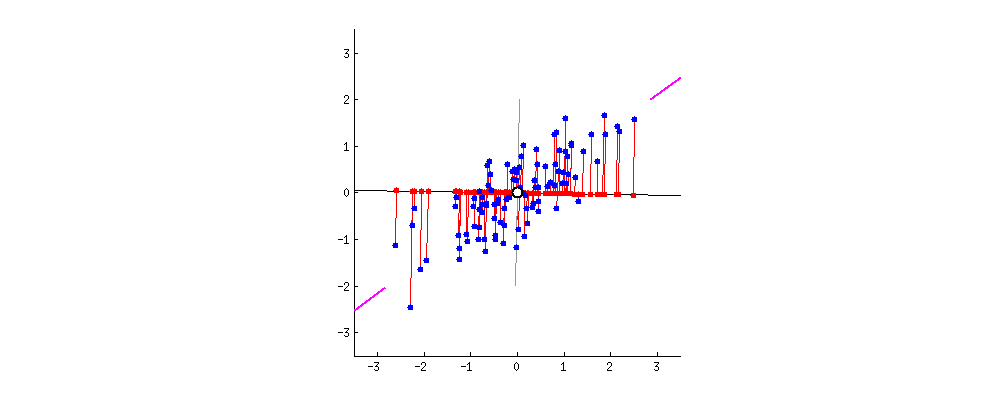
일반적으로 가장 분산(고유벡터; Eigenvalue)이 큰 축 하나만 사용 or 축 2개 사용

• 공분산? 두 feature가 얼마나 동시에 같은 방향으로 변하는가.

• 고유벡터를 얻는다? == 연관있는 피쳐쌍의 기저를 얻는다.

• 공분산(cov) 행렬은 원본 데이터 feature의 개수가 n이면 n X n 크기의 cov행렬이 생기게 된다.

PCA는 피쳐선택, 피쳐수감소에 주로 쓰이지만, 이미지 압축에도 사용된다.

• PCA 장점

​ 데이터 feature차원이 크면 데이터 직관하기 힘든데, PCA를 사용하면 도움이 된다.

• PCA 단점

1. 공분산이 중요하기 때문에, 분산이 작은게 좋은 데이터에 사용하기에 부적합하다.

2. 데이터의 분산이 직교하지 않으면 적합하지 않다.

LDA(Linear Discriminant Analysis)

클래스 간 중심거리(분산)는 크고, 클래스 내 분산은 작게 학습시킨다

분자는 클래스 중심간의 거리이며, 분모는 동일 클래스 내의 분산이다.

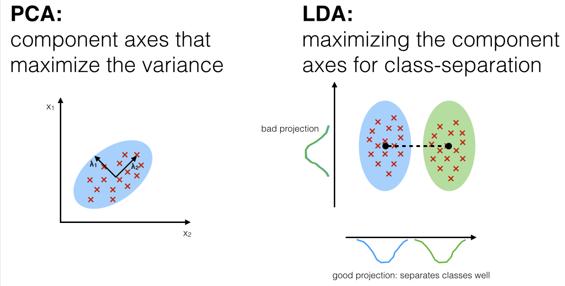
LDA에 의해 생성되는 vector로 projection(사영)하면, 클래스 판별이 잘 된다.

• LDA 용도

1. class 3개 이상도 가능
2. feature selection도 가능
3. 분류도 가능 (그렇지만 classifier은 아니다.)

• LDA 한계점

​ 비선형분포인 데이터에서는 적합하지 않다.

• PCA과 LDA차이점

​ PCA는 종합적인 전체 데이터를 잘 설명하는 축을 찾는게 목표
(클래스 레이블을 고려하지 않는다.)

​ LDA는 클래스 레이블을 고려하여 분류를 잘해주는 축을 찾는 것이 목표이다.

참고한 사이트

https://m.blog.naver.com/kiakass/222200041769

https://darkpgmr.tistory.com/106