03-03. 정밀도와 재현율

위키북스의 파이썬 머신러닝 완벽 가이드 책을 토대로 공부한 내용입니다.

---

1. 정밀도와 재현율

---

정밀도와 재현율은 Positive dataset의 예측 성능에 좀 더 초점을 맞춘 평가 지표이다.

정밀도 = ${TP \over (FP\ +\ TP)}$

재현율 = ${TP \over (FN\ +\ TP)}$

정밀도는 예측을 Positive로 한 대상중에 예측값과 실제값이 Positive로 일치한 데이터의 비율을 뜻한다. Positive 예측 성능을 더욱 정밀하게 측정하기 위한 평가 지표로 양성 예측도라고도 불린다.

재현율은 실제값이 Positive인 대상중에 예측값과 실제값이 Positive로 일치한 데이터의 비율을 뜻한다. 민감도(Sensitivity) 또는 TPR(True Positive Rate)라고도 불린다.

재현율이 중요 지표인 경우는 암 판단 모델이나 금융 사기 적발 모델과 같이 실제 Positive 양성 데이터를 Negative로 잘못 판단하게 되면 업무상 큰 영향이 발생하는 경우이다. 따라서 보통 재현율이 정밀도보다 상대적으로 중요한 업무가 많지만, 스팸메일 여부를 판단하는 모델과 같은 경우는 정밀도가 더 중요한 지표이다.

• 재현율이 상대적으로 더 중요한 지표인 경우는 실제 Positive 양성인 데이터 예측을 Negative 음성으로 잘못 판단하게 되면 업무상 큰 영향이 발생하는 경우
• 정밀도가 상대적으로 더 중요한 지표인 경우는 실제 Negative 음성인 데이터 예측을 Positive 양성으로 잘못 판단하게 되면 업무상 큰 영향이 발생하는 경우

재현율과 정밀도는 둘 다 TP를 높이는데 초점을 맞추고 있는 점이 같지만, 재현율은 FN을 낮추는 데, 정밀도는 FP를 낮추는 데 초점을 맞춘다는 점이 다르다. 이 특성때문에 재현율과 정밀도는 서로 보완적인 지표로 분류 모델의 성능을 평가하는데 적용되며, 둘 다 높은 수치를 얻는 것이 가장 좋은 성능을 의미한다. 반면 둘 중 어느 한 평가 지표만 매우 높고, 다른 하나는 매우 낮은 결과를 보이는 것은 바람직하지않다.

사이킷런은 정밀도 계산을 위해 precision_score()를, 재현율 계산을 위해 recall_score()를 API로 제공한다. 평가를 간편하게 적용하기 위해 confusion matrix, accuracy, precision, recall 등의 평가를 한번에 호출하는 get_clf_eval() 함수를 만들었다.

from sklearn.metrics import accuracy_score, precision_score , recall_score , confusion_matrix

def get_clf_eval(y_test , pred):
    confusion = confusion_matrix( y_test, pred)
    accuracy = accuracy_score(y_test , pred)
    precision = precision_score(y_test , pred)
    recall = recall_score(y_test , pred)
    print('오차 행렬')
    print(f'TN {confusion[0][0]}\t/ FP {confusion[0][1]}')
    print(f'FN {confusion[1][0]}\t/ TP {confusion[1][1]}')
    print('정확도: {0:.4f}, 정밀도: {1:.4f}, 재현율: {2:.4f}'.format(accuracy , precision ,recall))

그리고 로지스틱 회귀 기반으로 타이타닉 생존자 예측을 수행한 후 위의 함수로 평가하였다.

import numpy as np
import pandas as pd

from sklearn.model_selection import train_test_split 
from sklearn.linear_model import LogisticRegression

# 원본 데이터를 재로딩, 데이터 가공, 학습데이터/테스트 데이터 분할. 
titanic_df = pd.read_csv('/content/drive/MyDrive/pymldg-rev/2장/titanic_train.csv')
y_titanic_df = titanic_df['Survived']
X_titanic_df= titanic_df.drop('Survived', axis=1)
X_titanic_df = transform_features(X_titanic_df)

X_train, X_test, y_train, y_test = train_test_split(X_titanic_df, y_titanic_df, test_size=0.20, random_state=11)

lr_clf = LogisticRegression()

lr_clf.fit(X_train , y_train)
pred = lr_clf.predict(X_test)
get_clf_eval(y_test , pred)

[output]

---

2. 정밀도/재현율 Trade-off

---

분류 모델이 사용될 업무의 특성을 고려하여 정밀도와 재현율 중 더 강조돼야 할 부분을 결정하기 위한 임계값(Threshold)를 조정해 정밀도나 재현율의 수치를 높일 수 있다. 하지만 정밀도와 재현율은 상호 보완적인 평가 지표이기 때문에 이 두 지표에는 트레이드오프(Trade-off)가 존재하며, 이를 정밀도/재현율의 트레이드오프라고 부른다.

사이킷런의 분류 알고리즘은 예측 데이터가 특정 label에 속하는지를 계산하디 위해 먼저 각각의 label별 결정 확률을 구한 후, 더 높은 확률의 label로 예측한다. 일반적으로 이진 분류에서는 결정 확률의 임계값이 0.5로 정해지고 확률이 크면 Positive, 낮으면 Negative로 결정한다. 사이킷런은 각각의 데이터 별 예측 확률을 반환하는 method로 predict_proba()를 제공한다. 학습이 완료된 Classifier 객체에서 호출이 가능하며 test feature dataset을 parameter로 입력하면 test faeture에 대한 개별 class의 예측 확률을 반환한다.

• 입력 파라미터
  • predict() method와 동일하게 보통 test feature dataset을 입력
• 반환 값
  • 개별 class의 예측 확률을 ndarray m x n (m:입력 값의 레코드 수, n:class 값 유형) 형태로 반환
  • 입력 test dataset의 표본 개수가 100개이고, 예측 class 값 유형이 2개(이진 분류)라면 반환값은 100 x 2 ndarray
  • 각 row는 개별 class의 예측 확률이고, 이진 분류에서 첫번째 column은 0 Negative의 확률, 두번째 column은 1 Positive의 확률이다.

predict_proba() method를 사용하여 타이타닉 생존자 예측 모델의 예측 확률을 확인하였다.

pred_proba = lr_clf.predict_proba(X_test)
pred  = lr_clf.predict(X_test)
print('pred_proba() 결과 Shape : {0}'.format(pred_proba.shape))
print('='*60)
print('pred_proba array에서 앞 3개만 샘플로 추출 :')
print('-'*60)
print('Negative (0)\t\tPositive (1)')
print('-'*60)
for i in range(3):
    print(f'{pred_proba[i][0]}\t{pred_proba[i][1]}')
print('='*60)

# 예측 확률 array 와 예측 결과값 array 를 concatenate 하여 예측 확률과 결과값을 한눈에 확인
pred_proba_result = np.concatenate([pred_proba , pred.reshape(-1,1)],axis=1)
print('두개의 class 중에서 더 큰 확률을 클래스 값으로 예측 :')
print('-'*60)
print('Negative (0)\t\tPositive (1)\t\tPrediction')
print('-'*60)
for i in range(3):
    print(f'{pred_proba_result[i][0]}\t{pred_proba_result[i][1]}\t{pred_proba_result[i][2]}')
print('='*60)

[output] 사실 predict method는 predict_proba() method에 기반하여 생성된 API이다. predict_proba() method의 결과로 반환된 배열에서 더 높은 확률을 가진 column의 위치를 받아서 최종적으로 예측 class를 결정하는 API이다.

---

3. Binarizer의 threshold 조절

---

사이킷런의 predict()는 predict_proba() method가 반환하는 확률값을 가진 ndarray에서 정해진 임계값(default=0.5)을 만족하는 column 위치를 최종 예측 class로 결정한다. 이러한 로직을 구현하기 위해 Binarizer 클래스를 이용하였다. 특정 threshold 값을 변수로 설정하여 Binarizer 클래스를 객체로 생성하고 fit_transform method를 사용하여 threshold 보다 크면 1, 작으면 0으로 반환한다.

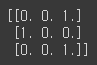
from sklearn.preprocessing import Binarizer

X = [[ 1, -1,  2],
     [ 2,  0,  0],
     [ 0,  1.1, 1.2]]

# threshold 기준값보다 같거나 작으면 0을, 크면 1을 반환
binarizer = Binarizer(threshold=1.1)                     
print(binarizer.fit_transform(X))

[output]
이제 Binarizer를 이용하여 사이킷런 predict()의 의사(pseudo) 코드를 만들 수 있다.

• threshold = 0.5

from sklearn.preprocessing import Binarizer

# Binarizer의 threshold 설정값. 분류 결정 임곗값임.  
custom_threshold = 0.5

# predict_proba( ) 반환값의 두번째 컬럼 , 즉 Positive 클래스 컬럼 하나만 추출하여 Binarizer를 적용
pred_proba_1 = pred_proba[:,1].reshape(-1,1)

binarizer = Binarizer(threshold=custom_threshold).fit(pred_proba_1) 
custom_predict = binarizer.transform(pred_proba_1)

get_clf_eval(y_test, custom_predict)

[output]

• threshold = 0.4

# Binarizer의 threshold 설정값을 0.4로 설정. 즉 분류 결정 임곗값을 0.5에서 0.4로 낮춤 

custom_threshold = 0.4
pred_proba_1 = pred_proba[:,1].reshape(-1,1)
binarizer = Binarizer(threshold=custom_threshold).fit(pred_proba_1) 
custom_predict = binarizer.transform(pred_proba_1)

get_clf_eval(y_test , custom_predict)

[output] threshold가 0.4로 낮아지니까 재현율이 올라가고, 정밀도가 떨어졌다. 그 이유는 분류 결정의 threshold는 Positive 예측값을 결정하는 확률의 기준이 되기 때문이다. 확률이 0.5가 아닌 0.4부터 Positive로 예측하기 때문에 threshold를 낮출수록 True 값이 많아지게 되고, Positive로 예측하는 경우가 많아지기 때문에 실제 Positive를 Negative로 예측하는 횟수가 감소하게 되어 재현율이 높아진다.

• threshold = 0.4 ~ 0.6 (in steps of 0.05)

# 테스트를 수행할 모든 임곗값을 리스트 객체로 저장. 
thresholds = [0.4, 0.45, 0.50, 0.55, 0.60]

def get_eval_by_threshold(y_test , pred_proba_c1, thresholds):
    # thresholds list객체내의 값을 차례로 iteration하면서 Evaluation 수행.
    for custom_threshold in thresholds:
        binarizer = Binarizer(threshold=custom_threshold).fit(pred_proba_c1) 
        custom_predict = binarizer.transform(pred_proba_c1)
        print('임곗값:',custom_threshold)
        print('-'*60)
        get_clf_eval(y_test , custom_predict)
        print('='*60)
      
get_eval_by_threshold(y_test ,pred_proba[:,1].reshape(-1,1), thresholds )

[output] 위의 결과에 따르면 threshold가 0.45인 경우가 default(threshold=0.5)인 경우와 비교해서 정확도는 동일하고, 정밀도는 약간 떨어졌으며 재현율이 올랐다. 만약 재현율을 향상시키면서 다른 수치를 약간 감소시켜야 하는 경우라면 threshold 값은 0.45가 가장 적당할 것이다.

---

4. precision_recall_curve()

---

사이킷런은 threshold 변화에 따른 정밀도와 재현율을 구할 수 있게 해주는 precision_recall_curve() API를 제공한다.

• 입력 파라미터
  • y_true : 실제 class 값 배열 (배열 크기 = [데이터 건수])
  • probas_pred : Positive column의 예측 확률 배열 (배열 크기=[데이터 건수])
• 반환 값
  • 정밀도 : 임계값별 정밀도 값을 배열로 반환
  • 재현율 : 임계값별 재현율 값을 배열로 반환
  • 일반적으로 0.11 ~ 0.95 정도의 threshold 값을 담은 ndarray와 이 threshold에 해당하는 정밀도와 재현율 값을 담은 ndarray를 반환

from sklearn.metrics import precision_recall_curve

# 레이블 값이 1일때의 예측 확률을 추출 
pred_proba_class1 = lr_clf.predict_proba(X_test)[:, 1] 

# 실제값 데이터 셋과 레이블 값이 1일 때의 예측 확률을 precision_recall_curve 인자로 입력 
precisions, recalls, thresholds = precision_recall_curve(y_test, pred_proba_class1 )
print('반환된 분류 결정 임곗값 배열의 Shape:', thresholds.shape)
print('반환된 precisions 배열의 Shape:', precisions.shape)
print('반환된 recalls 배열의 Shape:', recalls.shape)

print("thresholds 5 sample:", thresholds[:5])
print("precisions 5 sample:", precisions[:5])
print("recalls 5 sample:", recalls[:5])

# 반환된 임계값 배열 로우가 147건이므로 샘플로 10건만 추출하되, 임곗값을 15 Step으로 추출. 
thr_index = np.arange(0, thresholds.shape[0], 15)
print('샘플 추출을 위한 임계값 배열의 index 10개:', thr_index)
print('샘플용 10개의 임곗값: ', np.round(thresholds[thr_index], 2))

# 15 step 단위로 추출된 임계값에 따른 정밀도와 재현율 값 
print('샘플 임계값별 정밀도: ', np.round(precisions[thr_index], 3))
print('샘플 임계값별 재현율: ', np.round(recalls[thr_index], 3))

[output] 결과를 보면 threshold가 증가할수록 정밀도는 높아지면서 재현율은 동시에 낮아지는 것을 알 수 있다. precision_recall_curve() API는 이 결과를 시각화하는데 이용할 수 있다.

import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
%matplotlib inline

def precision_recall_curve_plot(y_test , pred_proba_c1):
    # threshold ndarray와 이 threshold에 따른 정밀도, 재현율 ndarray 추출. 
    precisions, recalls, thresholds = precision_recall_curve( y_test, pred_proba_c1)
  
    # X축을 threshold값으로, Y축은 정밀도, 재현율 값으로 각각 Plot 수행. 정밀도는 점선으로 표시
    plt.figure(figsize=(8,6))
    threshold_boundary = thresholds.shape[0]
    plt.plot(thresholds, precisions[0:threshold_boundary], linestyle='--', label='precision')
    plt.plot(thresholds, recalls[0:threshold_boundary],label='recall')
  
    # threshold 값 X 축의 Scale을 0.1 단위로 변경
    start, end = plt.xlim()
    plt.xticks(np.round(np.arange(start, end, 0.1),2))
  
    # x축, y축 label과 legend, 그리고 grid 설정
    plt.xlabel('Threshold value'); plt.ylabel('Precision and Recall value')
    plt.legend(); plt.grid()
    plt.show()
  
precision_recall_curve_plot( y_test, lr_clf.predict_proba(X_test)[:, 1] )

[output] 그래프에서 볼 수 있듯이 정밀도와 재현율에 trede-off가 존재하며 이 모델의 경우 약 0.45 정도의 threshold에서 재현율과 정밀도가 비슷해지는 것을 볼 수 있다.

---

5. 정밀도와 재현율의 맹점

---

threshold의 변경은 업무 환경에 맞게 2개의 수치를 상호 보완할 수 있는 수준에서 적용돼야 한다. 단순히 하나의 성능 지표 수치를 높이기 위한 수단으로 사용돼서는 안된다. 다음 방법들은 2개의 수치 중 하나를 극단적으로 높이는 방법이지만 사실 단순한 숫자 놀음에 불과하다.

• 정밀도가 100%가 되는 방법
  : 확실한 기준이 되는 경우만 Positive로 예측하고, 나머지는 Negative로 예측한다. 정밀도 = TP / (TP + FP) 이기 때문에 FP를 0으로만 만들면 정밀도는 100%가 되기 때문에 확실한 경우만 Positive로 예측하고 나머지는 무조건 Negative로 예측하는 방법이다.
• 재현율이 100%가 되는 방법
  : 재현율 = TP / (TP + FN) 이기 때문에 FN을 0으로 만들면 재현율은 100%로 얻을 수 있다. 따라서 모든 결과값을 Positive로 예측하면 된다.

위 방법들과 같이 정밀도와 재현율은 어느 한쪽만을 극단적으로 높이는 수치 조작이 가능하기 때문에 하나의 수치만 높고 다른 하나의 수치는 낮은 경우는 성능이 좋지 않은 분류로 평가해야한다.