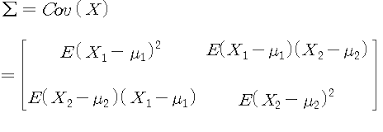위키북스의 파이썬 머신러닝 완벽 가이드 책을 토대로 공부한 내용입니다.
1. PCA 개요
PCA(Principal Component Analysis)는 가장 대표적인 차원 축소 방법이다. PCA는 여러 변수 간에 존재하는 상관관계를 이용하여 이 변수들의 상관관계를 대표하는 주성분(Principal Component)을 추출해 차원을 축소하는 방법이다. 차원이 축소할 때 기존의 정보가 유실되지만 PCA를 이용할 때 유실되는 정보가 최소화된다. PCA는 데이터가 주어져 있을 경우 그 데이터 각각의 값들에 대한 정보를 파악하는 것이 아니라 데이터의 분포에 대한 정보를 파악하는 것으로 가장 높은 분산을 가지는 데이터의 축을 찾아 이 축이 차원을 축소하게 되는 PCA의 주성분이 된다. 즉, 분산이 데이터의 특성을 가장 잘 나타내는 것으로 간주하고 있다.
PCA는 먼저 가장 큰 데이터 변동성(Variance)을 기반으로 첫번째 벡터 축을 생성하고, 두 번째 축은 이 벡터 축에 직각이 되는 벡터(직교 벡터)를 축으로 한다. 세번째 축은 다시 첫번째와 두번째 축에 직각이 되는 벡터를 축으로 설정하며 이러한 방식으로 축을 생성한다. 이렇게 생성된 벡터 축에 원본 데이터를 투영하면 벡터 축 개수만큼의 차원으로 차원 축소가 이루어진다. 즉, PCA는 이처럼 원본 데이터의 feature 개수에 비해 작은 주성분으로 원본 데이터의 총 변동성을 대부분 설명할 수 있는 분석법이다. 이론상으로 주성분은 최대 feature 개수만큼의 차원을 가질 수 있지만 차원 축소를 목적으로 실행하며 벡터 축이 점점 생성될수록 의미가 크지 않기 때문에 사용자가 적당히 축소할 차원 수를 설정한다.
PCA를 선형대수 관점에서 해석해보면, 입력 데이터의 공분산 행렬(Covariance Matrix)을 고유값 분해하고, 이렇게 구한 고유벡터에 입력 데이터를 선형 변환하는 것이다. 이 고유벡터가 PCA의 주성분 벡터로서 입력 데이터의 분산이 큰 방향을 나타낸다. 고유값(eigenvalue)은 이 고유벡터(eigenvector)의 크기를 나타내며, 동시에 입력 데이터의 분산을 나타낸다. 일반적으로 선형 변환은 특정 벡터에 션형 변환 행렬 A를 곱해 새로운 벡터로 변환하는 것을 의미하며, 특정 벡터를 한 공간에서 다른 공간으로 투영하는 개념으로도 볼 수 있다. 보통 분산은 한 개의 특정 변수에 대해 데이터의 변동을 의미하지만, 공분산은 두 변수 간의 변동을 의미한다.
공분산 행렬은 위 이미지와 같이 구할 수 있으며, 정방 행렬(Diagonal Matrix)이면서 대칭 행렬(Symmetric Matrix)이다. 이렇게 정방 행렬이면서 대칭 행렬이면 고유값 분해를 통해 교유 벡터를 직교 행렬(othogonal metrix)로, 고유값을 정방 행렬로 대각화할 수 있다. 따라서 공분산 행렬도 고유값 분해를 통해 나타낼 수 있다. 여기서 고유 벡터를 으로 나타낼 수 있으며 이 가장 큰 분산의 방향을 가진 고유 벡터이다.
2. iris 데이터 세트 PCA 변환
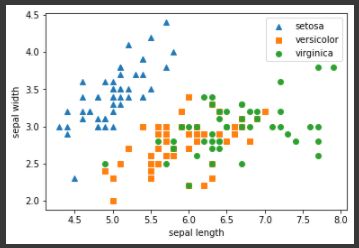
PCA는 많은 속성으로 구성된 원본 데이터를 핵심을 구성하는 데이터로 압축한 것이다. iris 데이터는 sepal length, sepal width, petal length, petal width의 4개의 속성으로 이루어져 있다. 이 4개의 속성을 PCA를 통해 2개의 차원으로 압축하여 데이터가 어떻게 달라지는지 확인해보겠다. 먼저 dataset의 분포를 확인하기 위해 sepal length, sepal width를 두 축으로 하여 2차원으로 시각화해보겠다.
from sklearn.datasets import load_iris import pandas as pd import matplotlib.pyplot as plt %matplotlib inline # 사이킷런 내장 데이터 셋 API 호출 iris = load_iris() # 넘파이 데이터 셋을 Pandas DataFrame으로 변환 columns = ['sepal_length','sepal_width','petal_length','petal_width'] irisDF = pd.DataFrame(iris.data , columns=columns) irisDF['target']=iris.target #setosa는 세모, versicolor는 네모, virginica는 동그라미로 표현 markers=['^', 's', 'o'] #setosa의 target 값은 0, versicolor는 1, virginica는 2. 각 target 별로 다른 shape으로 scatter plot for i, marker in enumerate(markers): x_axis_data = irisDF[irisDF['target']==i]['sepal_length'] y_axis_data = irisDF[irisDF['target']==i]['sepal_width'] plt.scatter(x_axis_data, y_axis_data, marker=marker,label=iris.target_names[i]) plt.legend() plt.xlabel('sepal length') plt.ylabel('sepal width') plt.show()[output]
Setota의 경우는 한쪽으로 일정하게 분포되어 있지만, Versicolor와 virginica의 경우는 분류가 어려운 복잡한 조건인 것을 알 수 있다. PCA를 통해 2개 속성으로 압축한 뒤 다시 시각화를 해보겠다.
PCA를 적용하기 전에 개별 속성을 함계 스케일링 하여 각 속성값이 동일한 스케일을 가지도록 하는것이 필요하다. PCA는 여러 속성 값을 연산해야 하므로 스케일에 영향을 받기 때문이다. 사이킷런의 StandardScaler를 이용해 평군이 0, 분산이 1인 표준 정규 분포로 iris dataset의 속성값들을 변환한다. 그 다음 사이킷런의 PCA 클래스를 통해 PCA를 적용하여 4차원의 데이터를 2차원의 PCA 데이터로 변환시킨다. PCA 클래스는 파라미터로 n_component를 입력받는데 이는 변환할 차원 수를 의미한다.
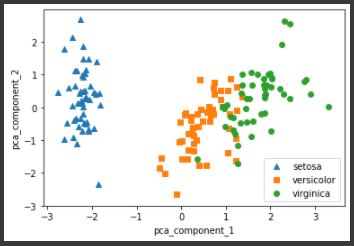
from sklearn.preprocessing import StandardScaler # Target 값을 제외한 모든 속성 값을 StandardScaler를 이용하여 표준 정규 분포를 가지는 값들로 변환 iris_scaled = StandardScaler().fit_transform(irisDF.iloc[:, :-1]) from sklearn.decomposition import PCA pca = PCA(n_components=2) #fit( )과 transform( ) 을 호출하여 PCA 변환 데이터 반환 pca.fit(iris_scaled) iris_pca = pca.transform(iris_scaled) print(iris_pca.shape) # PCA 환된 데이터의 컬럼명을 각각 pca_component_1, pca_component_2로 명명 pca_columns=['pca_component_1','pca_component_2'] irisDF_pca = pd.DataFrame(iris_pca, columns=pca_columns) irisDF_pca['target']=iris.target #setosa를 세모, versicolor를 네모, virginica를 동그라미로 표시 markers=['^', 's', 'o'] #pca_component_1 을 x축, pc_component_2를 y축으로 scatter plot 수행. for i, marker in enumerate(markers): x_axis_data = irisDF_pca[irisDF_pca['target']==i]['pca_component_1'] y_axis_data = irisDF_pca[irisDF_pca['target']==i]['pca_component_2'] plt.scatter(x_axis_data, y_axis_data, marker=marker,label=iris.target_names[i]) plt.legend() plt.xlabel('pca_component_1') plt.ylabel('pca_component_2') plt.show()[output]
PCA 변환 후에, Setosa 품종은 더욱 명확하게 구분이 가능하며 Versicolor와 Virginica도 서로 겹치는 부분이 일부 존재하지만 비교적 잘 구분되게 바뀌었다. 이렇게 바뀐 두 축이 원본 데이터의 변동성(분산)을 전체 변동성에서 얼마나 반영하는지 비율을 알아보겠다.
print(pca.explained_variance_ratio_)[output]
따라서 PCA를 2개 요소만 변환해도 전체 데이터의 변동성을 95% 설명할 수 있다. 이제 random forest를 적용하여 정확도 결과를 비교해보겠다.from sklearn.ensemble import RandomForestClassifier from sklearn.model_selection import cross_val_score import numpy as np rcf = RandomForestClassifier(random_state=156) scores = cross_val_score(rcf, iris.data, iris.target,scoring='accuracy',cv=3) print('원본 데이터 교차 검증 개별 정확도:',scores) print('원본 데이터 평균 정확도:', np.mean(scores))[output]
pca_X = irisDF_pca[['pca_component_1', 'pca_component_2']] scores_pca = cross_val_score(rcf, pca_X, iris.target, scoring='accuracy', cv=3 ) print('PCA 변환 데이터 교차 검증 개별 정확도:',scores_pca) print('PCA 변환 데이터 평균 정확도:', np.mean(scores_pca))[output]
원본 데이터를 사용한 예측 정확도와 PCA 변환 데이터를 사용한 예측 정확도를 비교해보면 PCA 변환 후 성능이 10% 더 떨어지게 된다. 10%의 정확도 하락은 비교적 큰 성능 수치의 감소지만, 4개 속성이 2개 속성으로 50% 감소한 것을 고려한다면 PCA 변환 후에도 원본 데이터의 특성을 상당 부분 유지하고 있음을 알 수 있다.
3. credit card 데이터 세트 PCA 변환
이번에는 좀 더 많은 feature를 가진 dataset을 적은 PCA component 기반으로 변환한 뒤, 예측 영향도가 어떻게 되는지 변환된 PCA dataset에 기반해서 비교해보겠다. 사용할 dataset은 UCI Machine Learning Repository에 있는 신용카드 고객 dataset(Credit Card Client Dataset)이다.
신용카드 dataset은 30000개의 record와 24개의 속성을 가지고 있다. 이 중 'default payment next month' 속성이 Target 값으로 '다음달 연체 여부'를 의미하며 '연체'일 경우 1, '정상남부'일 경우 0이다. 그리고 이 dataset은 23개의 속성 dataset이 있지만 각 속성끼리 상관도가 매우 높다. dataframe의 corr()를 이용하여 각 속성 간의 상관도를 구한 뒤 seabon의 heatmap으로 시각화하겠다.
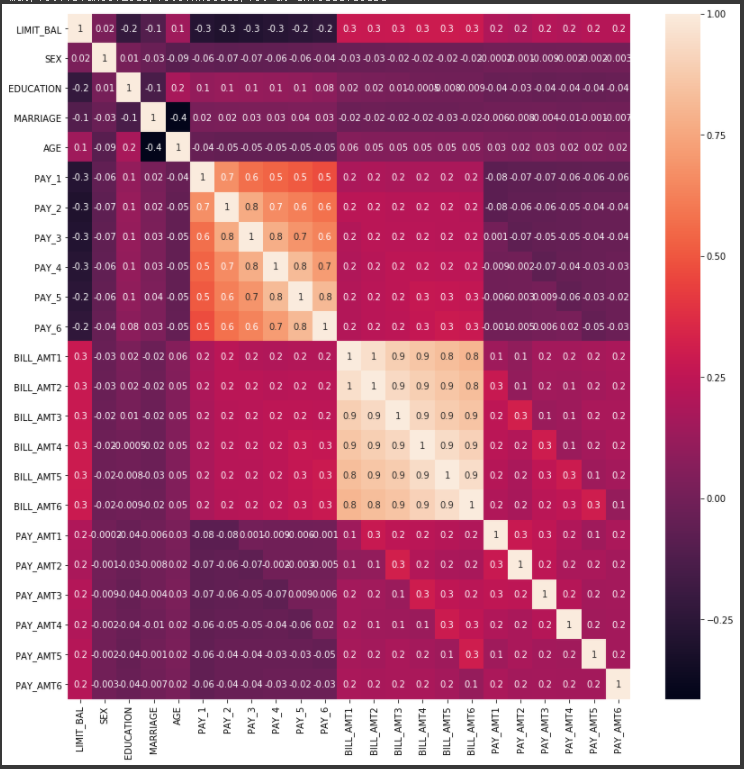
# header로 의미없는 첫행 제거, iloc로 기존 id 제거 import pandas as pd import seaborn as sns import matplotlib.pyplot as plt %matplotlib inline df = pd.read_excel('credit_card.xls', header=1, sheet_name='Data').iloc[0:,1:] df.rename(columns={'PAY_0':'PAY_1','default payment next month':'default'}, inplace=True) y_target = df['default'] X_features = df.drop('default', axis=1) corr = X_features.corr() plt.figure(figsize=(14,14)) sns.heatmap(corr, annot=True, fmt='.1g')[output]
BILL_AMT1 ~ BILL_ATM6 6개의 속성끼리의 상관도가 대부분 0.9 이상으로 매우 높은 것을 알 수 있으며, 0.9보다는 낮지만 PAY_1 ~ PAY_6 까지의 속성 역시 상관도가 매우 높다. 이렇게 높은 상관도를 가진 속성들은 소수의 PCA 만으로도 자연스럽게 이 속성들의 변동성을 수용할 수 있다. PCA를 통해 BILL_AMT1 ~ BILL_ATM6 6개의 속성을 2개의 component로 변환한 후 개별 component의 변동성 비율을 알아보겠다.from sklearn.decomposition import PCA from sklearn.preprocessing import StandardScaler #BILL_AMT1 ~ BILL_AMT6 까지 6개의 속성명 생성 cols_bill = ['BILL_AMT'+str(i) for i in range(1,7)] print('대상 속성명:',cols_bill) # 2개의 PCA 속성을 가진 PCA 객체 생성하고, explained_variance_ratio_ 계산 위해 fit( ) 호출 scaler = StandardScaler() df_cols_scaled = scaler.fit_transform(X_features[cols_bill]) X_features.loc[:, cols_bill] = df_cols_scaled pca = PCA(n_components=2) pca.fit(df_cols_scaled) print('PCA Component별 변동성:', pca.explained_variance_ratio_)[output]
2개의 PCA component 만으로 6개 속성의 변동성을 약 95% 이상 설명할 수 있으며 특히 PCA 축으로 90%의 변동성을 수용할 정도로 6개의 속성의 상관도가 매우 높다. 이제 random forest를 통해 원본 dataset과 6개의 component로 PCA 변환한 dataset의 예측 정확도를 비교해보겠다.import numpy as np from sklearn.ensemble import RandomForestClassifier from sklearn.model_selection import cross_val_score rcf = RandomForestClassifier(n_estimators=300, random_state=156) scores = cross_val_score(rcf, X_features, y_target, scoring='accuracy', cv=3 ) print('CV=3 인 경우의 개별 Fold세트별 정확도:',scores) print('평균 정확도:{0:.4f}'.format(np.mean(scores)))[output]
from sklearn.decomposition import PCA from sklearn.preprocessing import StandardScaler # 원본 데이터셋에 먼저 StandardScaler적용 scaler = StandardScaler() df_scaled = scaler.fit_transform(X_features) # 6개의 Component를 가진 PCA 변환을 수행하고 cross_val_score( )로 분류 예측 수행. pca = PCA(n_components=6) df_pca = pca.fit_transform(df_scaled) scores_pca = cross_val_score(rcf, df_pca, y_target, scoring='accuracy', cv=3) print('CV=3 인 경우의 PCA 변환된 개별 Fold세트별 정확도:',scores_pca) print('PCA 변환 데이터 셋 평균 정확도:{0:.4f}'.format(np.mean(scores_pca)))[output]
전체 23개의 속성의 약 25% 수준인 6개의 PCA component 만으로 원본 데이터를 기반으로 한 분류 예측 결과보다 약 1~2%의 성능 저하만 발생했다. 1~2%의 성능이 저하되는 것을 미비한 성능 저하로 보기 힘들지만 PCA의 뛰어난 압축 능력을 잘 보여주는 것이라고 생각된다. PCA는 차원 축소를 통해 데이터를 쉽게 인지하는데 활용될 수 있지만, 이보다 더 활발하게 적용되는 영역은 Computer Vision(CV) 분야이다. 특히 얼굴 인식의 경우 Eigen-face라고 불리는 PCA 변환으로 원본 얼굴 이미지를 변환해 사용하는 경우가 많다.