위키북스의 파이썬 머신러닝 완벽 가이드 책을 토대로 공부한 내용입니다.
1. SVD 개요
PCA의 경우 정방행렬만을 고유벡터로 분해할 수 있지만, SVD는 정방행렬 뿐만 아니라 행과 열의 크기가 다른 행렬에도 적용할 수 있다. 일반적으로 SVD는 특이값 분해로 불리며, m x n 크기의 행렬 A를 특이 벡터(singular vector)로 이루어진 행렬 U와 V, 대각 행렬 로 분해된다.
모든 특이 벡터는 서로 직교(orthogonal)하는 성질을 가지며, 대각 행렬 의 대각 성분이 행렬 A의 특이값이다.
일반적으로 는 m x n의 크기를 가지기 때문에 의 비대각 부분과 대각 원소중 특이값이 0인 부분도 모두 제거해주며 제거한 부분에 대응되는 U와 V의 원소도 같이 제거하여 차원을 줄인 상태로 SVD를 적용한다. 이렇게 간단한 형태로 SVD를 적용하면 A의 차원이 m x n일때, U의 차원을 m x p, 의 차원을 p x p, V의 차원을 n x p로 분해하게 된다. 이렇게 분해하는 방법을 Truncated SVD라고 한다.
2. SVD 를 이용한 행렬 분해
일반적인 SVD는 numpy나 scipy 라이브러리를 이용해 수행하며, 여기선 numpy의 SVD 연산을 통해 분해가 어떤 식으로 되는지 간단하게간단하게 알아보겠다.
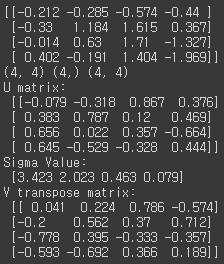
# numpy의 svd 모듈 import import numpy as np from numpy.linalg import svd # 4X4 Random 행렬 a 생성 np.random.seed(121) a = np.random.randn(4,4) print(np.round(a, 3)) U, Sigma, Vt = svd(a) print(U.shape, Sigma.shape, Vt.shape) print('U matrix:\n',np.round(U, 3)) print('Sigma Value:\n',np.round(Sigma, 3)) print('V transpose matrix:\n',np.round(Vt, 3))[output]
행렬의 개별 row vector끼리 의존성을 없애기 위해 랜덤으로 생성한 행렬 a에 SVD를 적용하여 U, Sigma, Vt를 도출했다. Sigma는 행렬의 대각에 위치만 값을 가지므로을 가지므로 1차원 행렬로 표현한다. 이렇게 분해된 행렬들을 이용해 다시 원본 행렬로 복원되는지 확인해보겠다.# Sima를 다시 0 을 포함한 대칭행렬로 변환 Sigma_mat = np.diag(Sigma) a_ = np.dot(np.dot(U, Sigma_mat), Vt) print(np.round(a_, 3))[output]
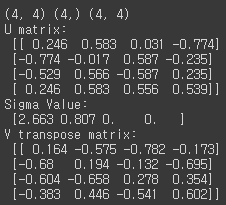
이번엔 data의 row vector 간의 의존성이 있을 경우 어떻게 Sigma 값이 변하고, 차원 축소가 어떻게 진행되는지 알아보기 위해 일부러 의존성을 부여한 다음 진행하였다.a[2] = a[0] + a[1] a[3] = a[0] # 다시 SVD를 수행하여 Sigma 값 확인 U, Sigma, Vt = svd(a) print(U.shape, Sigma.shape, Vt.shape) print('U matrix:\n',np.round(U, 3)) print('Sigma Value:\n',np.round(Sigma, 3)) print('V transpose matrix:\n',np.round(Vt, 3))[output]
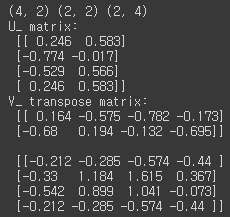
이전과 차원은 같지만 Sigma 값 중 2개가 0으로 나타나며, 이는 선형 독립인 row vector의 개수(rank)가 2개라는 의미이다. 그라고 이번엔 Sigma에 대응되는 부분만을 가지고 복원해보도록 하겠다.# U 행렬의 경우는 Sigma와 내적을 수행하므로 Sigma의 앞 2행에 대응되는 앞 2열만 추출 U_ = U[:, :2] Sigma_ = np.diag(Sigma[:2]) # V 전치 행렬의 경우는 앞 2행만 추출 Vt_ = Vt[:2] print(U_.shape, Sigma_.shape, Vt_.shape) # U, Sigma, Vt의 내적을 수행하며, 다시 원본 행렬 복원 print('U_ matrix:\n',np.round(U_, 3)) print('V_ transpose matrix:\n',np.round(Vt_, 3)) a_ = np.dot(np.dot(U_,Sigma_), Vt_) print('\n',np.round(a_, 3))[output]
3. Truncated SVD 를 이용한 행렬 분해
Truncated SVD는 numpy가 아닌 scipy에서만 지원된다. 임의의 행렬에 대해 우선 Normal SVD로 분해해본 뒤, 다시 Truncated SVD로 분해하여 Normal SVD와 Truncated SVD의 차원을 비교해보고, Truncated SVD로 분해하였을 때 복원이 어떻게 되는지 알아 보겠다.
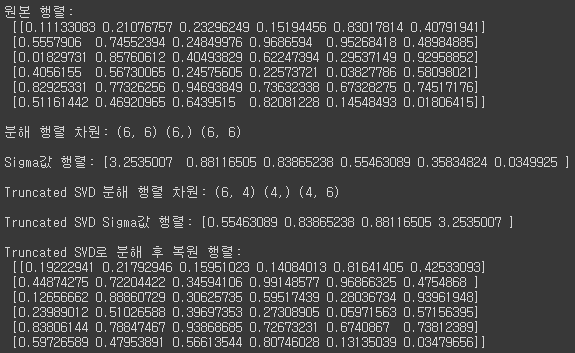
import numpy as np from scipy.sparse.linalg import svds from scipy.linalg import svd # 원본 행렬을 출력하고, SVD를 적용할 경우 U, Sigma, Vt 의 차원 확인 np.random.seed(121) matrix = np.random.random((6, 6)) print('원본 행렬:\n',matrix) U, Sigma, Vt = svd(matrix, full_matrices=False) print('\n분해 행렬 차원:',U.shape, Sigma.shape, Vt.shape) print('\nSigma값 행렬:', Sigma) # Truncated SVD로 Sigma 행렬의 특이값을 4개로 하여 Truncated SVD 수행. num_components = 4 U_tr, Sigma_tr, Vt_tr = svds(matrix, k=num_components) print('\nTruncated SVD 분해 행렬 차원:',U_tr.shape, Sigma_tr.shape, Vt_tr.shape) print('\nTruncated SVD Sigma값 행렬:', Sigma_tr) matrix_tr = np.dot(np.dot(U_tr,np.diag(Sigma_tr)), Vt_tr) # output of TruncatedSVD print('\nTruncated SVD로 분해 후 복원 행렬:\n', matrix_tr)[output]
n_components의 설정에 따라 차원수가 다르게 분해되며, Truncated SVD로 분해할 경우 완벽하지 않고 근사적으로 복원되는 것을 볼 수 있다.
4. 사이킷런 TruncatedSVD 클래스를 이용한 변환
사이킷런의 TruncatedSVD 클래스는 PCA 클래스와 유사하게 fit()과 transform()을 호출해 몇 개의 주요 component로 차원을 축소하여 변환한다. iris dataset을 이용하여 변환해 보겠다.
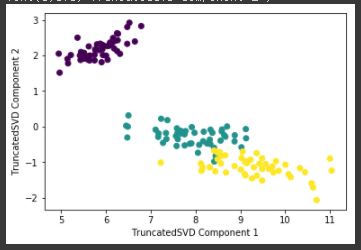
from sklearn.decomposition import TruncatedSVD from sklearn.datasets import load_iris import matplotlib.pyplot as plt %matplotlib inline iris = load_iris() iris_ftrs = iris.data # 2개의 주요 component로 TruncatedSVD 변환 tsvd = TruncatedSVD(n_components=2) tsvd.fit(iris_ftrs) iris_tsvd = tsvd.transform(iris_ftrs) # Scatter plot 2차원으로 TruncatedSVD 변환 된 데이터 표현. 품종은 색깔로 구분 plt.scatter(x=iris_tsvd[:,0], y= iris_tsvd[:,1], c= iris.target) plt.xlabel('TruncatedSVD Component 1') plt.ylabel('TruncatedSVD Component 2')[output]
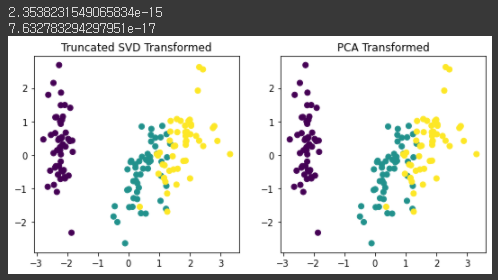
TruncatedSVD로 변환된 iris dataset도 PCA의 경우와 유사하게 변환되며 어느 정도 클러스터링이 가능할 정도로 각 변환되었다. 이번엔 스케일링을 한 뒤에 TruncatedSVD와 PCA 변환을 비교해보겠다.from sklearn.preprocessing import StandardScaler # iris 데이터를 StandardScaler로 변환 scaler = StandardScaler() iris_scaled = scaler.fit_transform(iris_ftrs) # 스케일링된 데이터를 기반으로 TruncatedSVD 변환 수행 tsvd = TruncatedSVD(n_components=2) tsvd.fit(iris_scaled) iris_tsvd = tsvd.transform(iris_scaled) # 스케일링된 데이터를 기반으로 PCA 변환 수행 pca = PCA(n_components=2) pca.fit(iris_scaled) iris_pca = pca.transform(iris_scaled) # TruncatedSVD 변환 데이터를 왼쪽에, PCA변환 데이터를 오른쪽에 표현 fig, (ax1, ax2) = plt.subplots(figsize=(9,4), ncols=2) ax1.scatter(x=iris_tsvd[:,0], y= iris_tsvd[:,1], c= iris.target) ax2.scatter(x=iris_pca[:,0], y= iris_pca[:,1], c= iris.target) ax1.set_title('Truncated SVD Transformed') ax2.set_title('PCA Transformed') print((iris_pca - iris_tsvd).mean()) print((pca.components_ - tsvd.components_).mean())[output]
결과적으로 두 변환 방법이 서로 동일한 것을 알 수 있다. 즉, 스케일링을 통해 데이터의 중심이 동일해지면 SVD와 PCA는 동일한 변환을 수행한다. 이는 PCA가 SVD 기반의 알고리즘이기 떄문이다. 하지만 PCA는 밀집 행렬(Dense Matrix)에 대한 변환만 가능하며, SVD는 희소 행렬(Sparse Matrix)에 대한 변환도 가능하다. 희소 행렬은 값의 대부분이 0으로 이루어진 행렬을 말한다.SVD는 PCA와 유사하게 컴퓨터 비전 영역에서 이미지 압축을 통한 패턴 인식과 신호 처리 분야에 사용된다. 또한 텍스트의 토픽 모델링 기법인 LSA(Latent Semantic Analysis)의 기반 알고리즘이다.