Abstract

• 무어의 법칙 끝남 -> 하드웨어 발전 속도 느려짐 -> 하드웨어를 효율적으로 활용하자.
• DNN은 메모리 및 많은 연산 필요 -> compression, hardware acceleration 필요
• trade off: processing efficiency vs application accuracy
• comprehensive한 survey가 필요함 (high level algorithm과 hardware desing 측면에서)
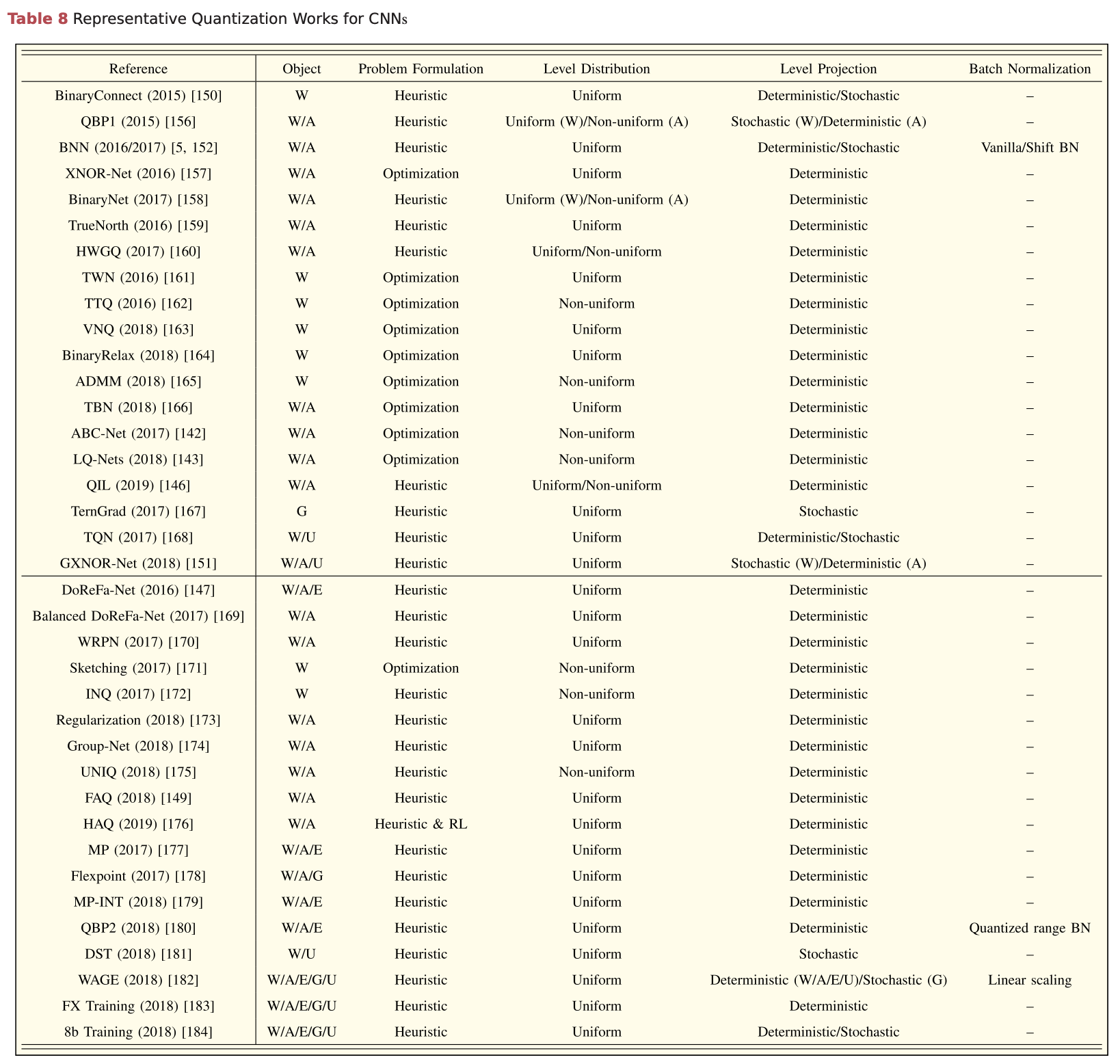
• mainstream compression approaches
  • compact model
  • tensor decomposition
  • data quantization
  • network sparsification
• 논문에서 각 토픽에서 소개하는 항목들
  • principle
  • evaluation metrics
  • sensitivity analysis
  • joint-way use
• 어떻게 leverage 할 것인가?
• 현존하는 issues
  • fair comparision
  • testing workloads
  • automatic compression
  • influence on security
  • framework / hardware-level support
  • possible challenges

Introduction, Motivation, and Overview

• Deep structure - DNN은 big-data로부터 high-level feature를 배울 수 있음
• Rule based와 구분됨
• DNN 성과가 좋은 이유
  • Model innovation
  • Data source
  • GPU 발전
• GPU -> 높은 parallelism & memory bandwidth
• edge device에 배포하려면 경량화 해야함
• algorithm & hardware의 interaction은 neural network compression domain에서 트렌드임
• algorithm 방식의 compression
  • Compact model -> smaller model base로 대체하는 것
  • Tensor decomposition -> bloat parameters를 작은 matrices 나 tensor로 대체
  • data quatization -> data bit 축소
  • network sparsification -> connection / neuron을 압축함
  • joint way -> 여러가지 방법 조합
• trade offs
  • scenario
  • compression ratio
  • model accuracy
  • hardware usability
• DNN에 효과적인 hardware도 관심이 많음
  • neural network accelerator라고 한다
• conventional한 DNN accelerator는 hardware architecture를 최적화함. -> parallelism과 memory access를 줄이기 위해
• 지금은 변한 이유
  • hardware optimization 단독은 upper bound에 도달함
  • compression algorithm이 잠재력을 가짐
• compression 기술의 다양성이 DNN accelerator 설계할 때 고려됨
• High-level algorithm optimization은 설계 가이드라인을 제공함
• low-lvel algorithm optimization은 effective algorithm에 feedback을 제공함 -> algorithm-hardware codesign
• 관련 논문이 엄청난 속도로 출간되는 중
• 접근 또한 다양함 -> 초보자가 big picture를 그리기 어렵다. -> 그래서 survey 한다.(correct recognition, analysis, comparison)
• 대부분의 compression approach와 hardware implementation을 다룸
• vertical comparison 수행
  • principle
  • compression ratio
  • accuracy degradation
  • sensitivity analysis
  • joint-way
• 그리고 advanced hardware solution도 설명함
  • 위의 compression techniques를 반영했음
  • 결론적으로 얻은 이득들 명시함
• 미래의 trend, 가능성, 도전과제들 표현
  

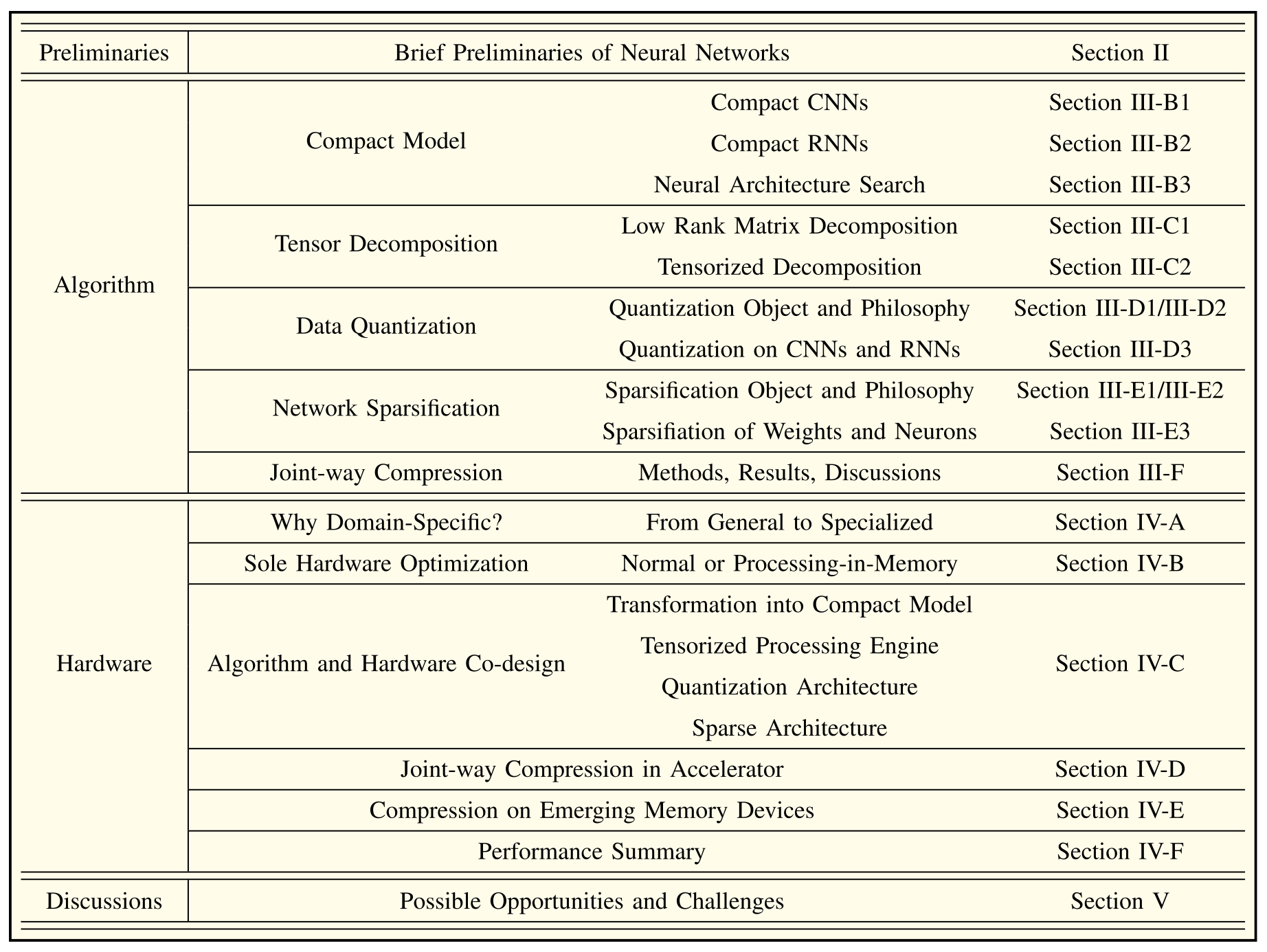
Brief Preliminaries of Neural Networks

• Neural Network의 배경 설명, 몇몇 모델 소개

  $y_i = \varphi(b_i + \sum_j x_j w_{ij} )$

• MLP: FC layer, ReLU

• CNN: Conv, Pool, FC layer

  • Multiple channels -> input data로부터 다양한 local feature 뽑기 위함
  • layer가 진행될수록 higher abstraction layer
  • Pool layer -> Down Sample 용도

Neural Network Compression: Algorithms

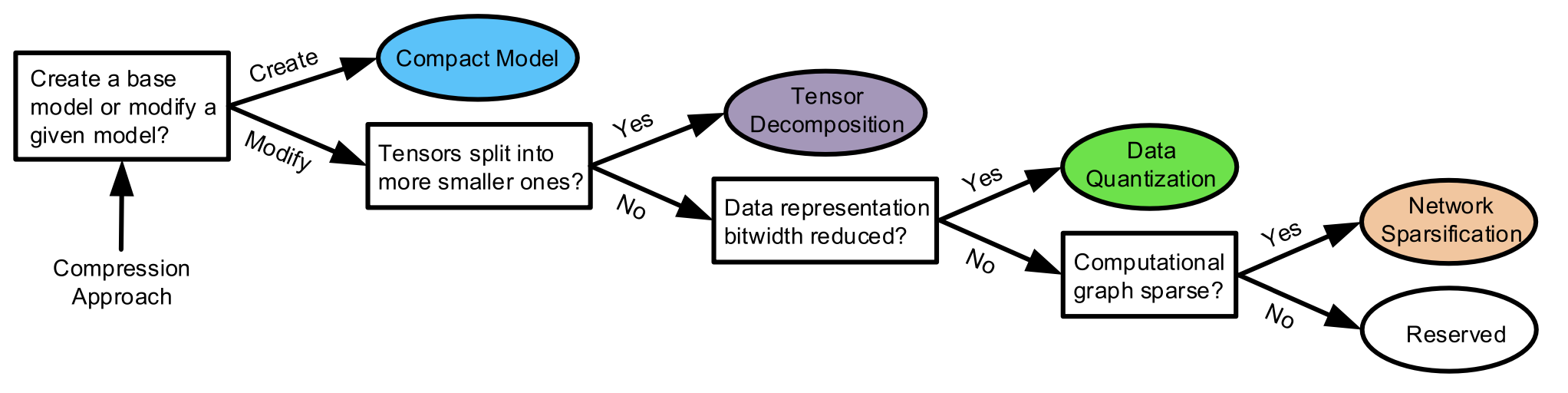
Taxonomy of Compression Approaches

• CNN, RNN 등 모델별로 분류하지 않은 이유는, compression 기법들이 대부분 모델과 상관없이 적용되기 때문
• 모델별로 분류하면 너무 혼란스러워짐

Compact Model

Compact CNNs

• skip connection, 3x3 등..
• Spatial, Channel 두 가지로 분류함
• 아래 링크와 유사한 내용들
  https://eehoeskrap.tistory.com/431

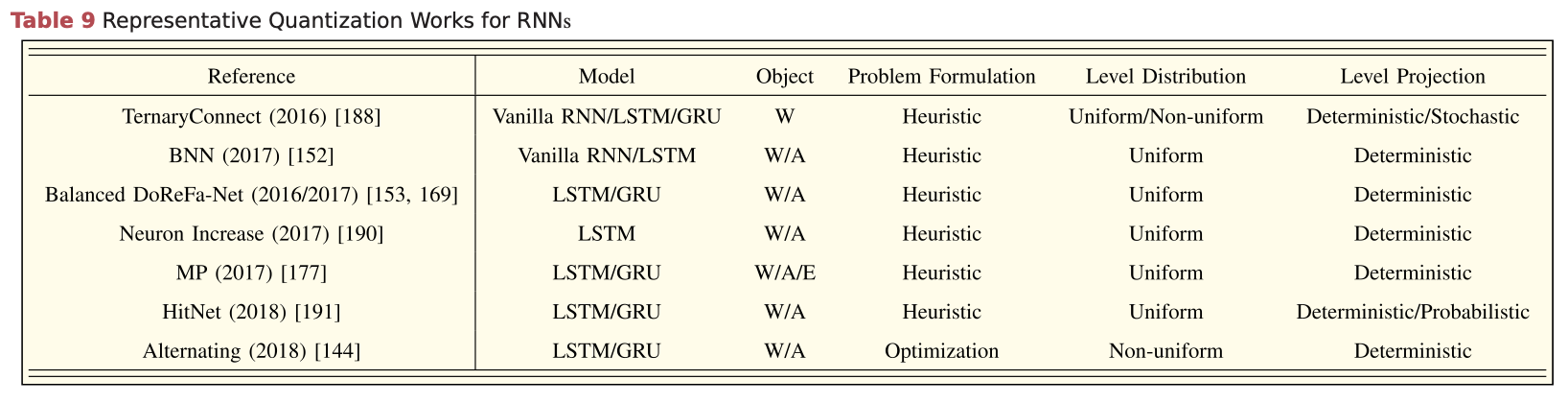
Compact RNNs

• Unit level, Network level로 분류하여 설명함
• LSTM -> GRU
• Quasi RNN
• Unitary RNN
• 등..

(NAS) Neural Architecture Search

• 앞에서 소개한 compression은 전문가에 의존.. NAS 필요성 대두
• RNN, Transformer 계열도 NAS에 대한 문헌들이 있지만, 이에 비해 CNN 모델에 대한 NAS 설명이 없기 때문에 여기서는 CNN 설명함
• Conventional NAS는 sequence generation problem으로 해보고 해결
  • RNN Controller 사용
  • RNN이 반복적으로 neural network 생성
  • 테스트 해 볼 모델이 엄청나게 많아짐
• CNN
  • Standard Conv, Asymmetric Conv, Depthwise-separable Cov, Dilated Conv, Pool, Activation function 등을 결정
• Search 제한 필요, -> basic building cell 부터 탐색

Search algorithm

• Generator produces an architecture
• Evaluator trains the network and evaluates the quality
• 종류
  • Random Search
  • Reinforcement Learning
  • Evolutionary Algorithms
  • Bayesian Optimization
  • Gradient-based Methods
• Reinforcement 기반 NAS
  • Q-learning
  • Policy-basd Reinforcement
• RL based와 Evolutionary methods는 discrete space에서 최적화한다
• Hypernetwork -> 훈련 없이 신경망의 weights 생성
• One-shot NAS methods -> single super-net의 훈련에 초점 맞춤. 추가적인 training cost 없음

Tensor Decomposition

Low-Rank Matrix Decomposition

Full-rank decomposition

$m$과 $n$이 유사하면 효과가 별로 없음.
$k<r$일 때,
$W \in \mathbb{R}^{m\times k}$ $H \in \mathbb{R}^{k\times n}$

$k$가 작을 때 근사 오차가 발생함.

• Full rank decomposition은 FC layer에서 neuron 수 차이가 클 때 효과적임
• Full rank decomposition은 낮은 rank, sparsity한 weight matrix인 경우 효과적임
• 사용하기 쉬움 -> CNN 적용 시 2D가 4D로 되지만 좋음
• 정확도 유지 어려움

Singular value decomposition (SVD)

$ A=U'S'V'^{T}$$U' \in \mathbb{R}^{m\times r}$ $V'^{T} \in \mathbb{R}^{r\times n}$ $S' \in \mathbb{R}^{r\times r}$
$\mathcal{O}(mn) \rightarrow \mathcal{O}(r(m+n+1))$

• error가 덜한 장점이 있다.
• Filter Group??
  • SVD -> one conv weight kernel -> 2 subkernels
• Softmax layer -> large vocabulary neural networks
• Fast decentralized gradient aggregation?? ( ring all-reduce)
  • distributed training을 할 때, PCA를 이용해서, weight gradient를 low-dimensional space로 만들어서 하는 것이..

Tensorized Decomposition

Discussion

Data Quantization

Quantization Data Object

Quantization Philosophy

Quantization on CNNs and RNNs

Results: Summary and Discussion