오차역전파

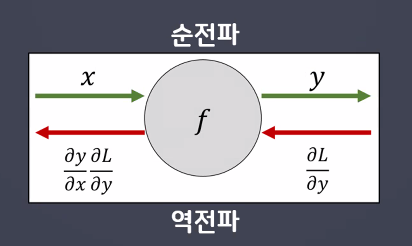
• 순전파
  입력 데이터를 입력층에서부터 출력층까지 정방향으로 이동시키며 출력 값을 예측해 나가는 과정

• 역전파
  출력층에서 발생한 에러를 입력층 쪽으로 전파시키면서 최적의 결과를 학습해 나가는 과정
  

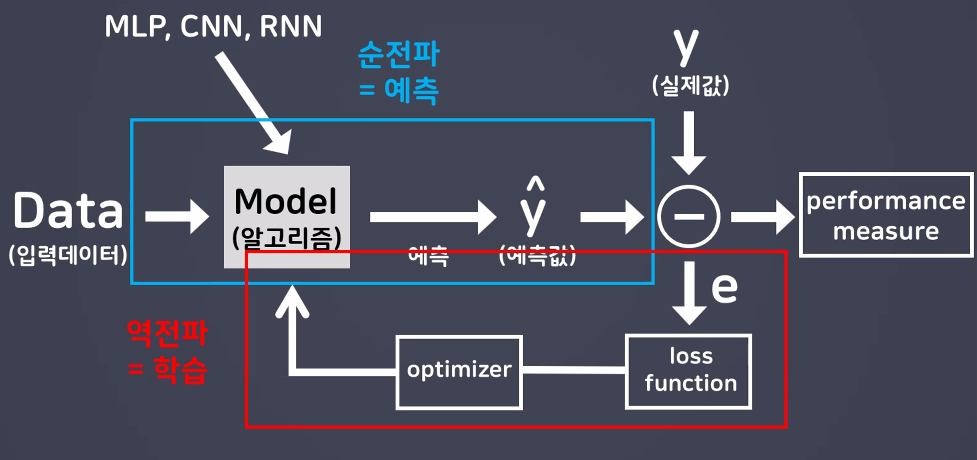
기울기 소실 문제 (Vanishing Gradient)

성능이 높은 모델을 만들기 위해 중간층을 늘렸지만 역전파 방식을 이용하게 되면서 sigmoid 함수를 미분한 값이 최대치가 0.25이므로 진행되면될수록 0.25를 곱하게되면서 실제결과와 다르게 경사하강법의 기울기가 0에 가까운 모습을 보이게 된다.

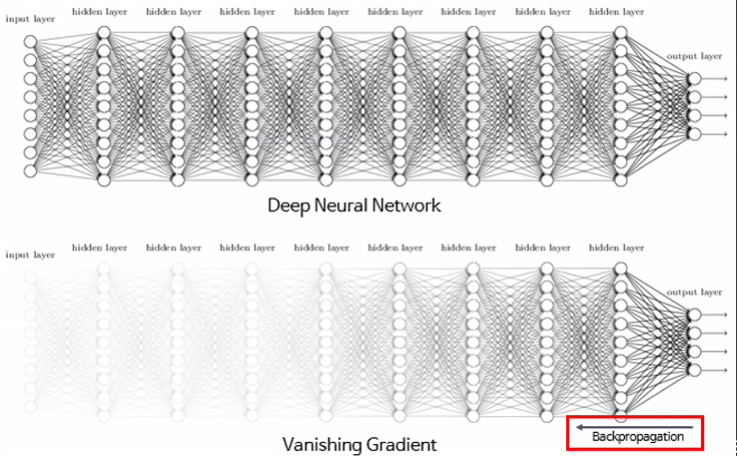
Sigmoid 함수

Sigmoid 함수의 미분 값은 입력값이 0일 때 가장 크지만 0.25에 불과하고 값이 크거나 작아짐에 따라 기울기는 거의 0에 수렴하는 것을 확인할 수 있다. 따라서, 역전파 과정에서 Sigmoid 함수의 미분값이 거듭 곱해지면 출력층과 멀어질수록 Gradient 값이 매우 작아질 수밖에 없다.
더불어, e(exponential)는 컴퓨터가 계산할 때 정확한 값이 아닌 근사값으로 계산해야 되기 때문에 역전파 과정에서 점차 학습 오차까지 증가하게 됩니다. 결국 sigmoid 함수를 활용하면 모델 학습이 제대로 이루어지지 않게 됩니다.

이를 해결하기 위한 방법으로 다양한 함수가 존재하는데,
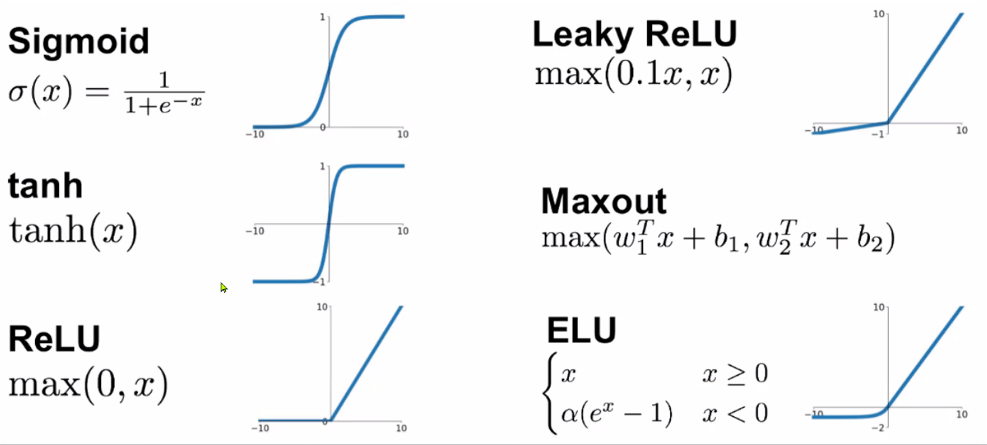이 글에서는 relu 함수에 대해 알아보자.

Relu 함수

현대 딥러닝 분야에서 가장 기초가 되는 함수로. 입력값이 음수이면 0을 출력하고 양수 값이면 그대로 흘려보내는 비교적 간단한 함수이다. Sigmoid 함수의 기울기 소실 문제를 해결해준 함수이다.
연산이 간편하고 Layer를 깊게 쌓을 수 있다는 장점이 있고, 단순한 함수임에도 성능이 잘 나오는 이유에 대해 해석이 분분하지만, 대체적으로 앙상블(ensamble) 효과로 해석한다.
참고로 ReLu 함수는 입력값이 너무 커지게 되면 모델이 입력 값에 편향이 될 수 있으므로
max값을 6 이하로 제한하는 방식으로 사용하기도 합니다.