Youtube : https://www.youtube.com/watch?v=BgB2NB7fLiM&list=PLetSlH8YjIfXMOuS4piqzJRvSZorDnNUm&index=7
1. 로지스틱 회귀가 등장한 이유
: 1/0(발생, 비발생)의 결과값을 내놓기 위해서 선형 회귀식은 적절하지 않음.
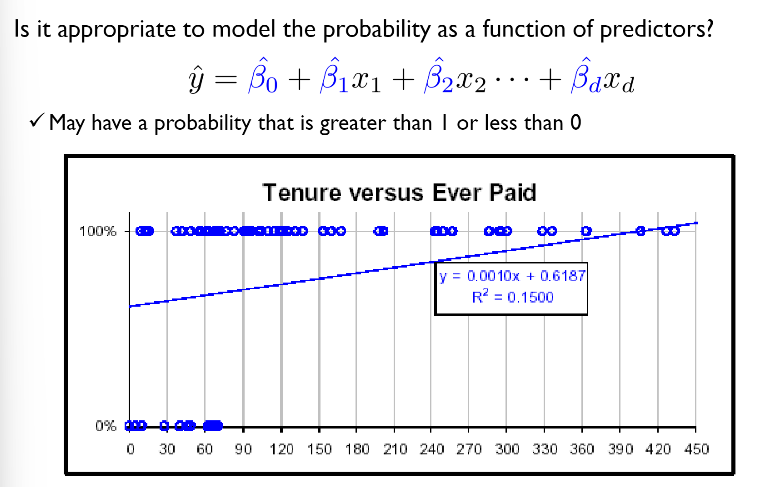파란색 선형회귀선이 이 데이터 분포를 잘 설명하느냐? 아니오.
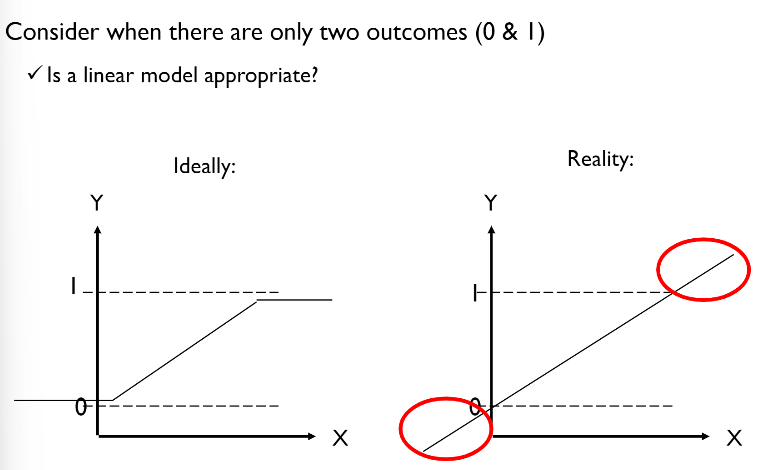
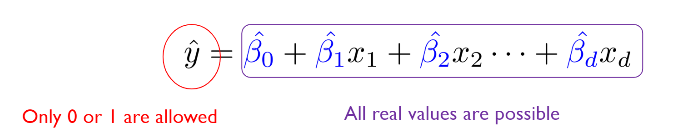0/1의 아웃풋을 갖기를 바라는 반면, 선형회귀의 아웃풋은 음의 무한대부터 양의 무한대까지임. 즉, 좌변과 우변의 범위가 달라짐.
2. 로지스틱 회귀의 목적
: 0/1 아웃풋을 내기 위한 설명 변수들의 함수를 찾는 것 (=출력값이 특정 범주에 속할 확률을 예측함)
어떻게?
- 선형 회귀와 같이 y 값을 직접 사용하지 않고, "Logit function"이라고 불리는 y 값을 사용함
- Logit function : 설명 변수들에 대한 선형 모형으로 추정
3. 로그 승산(log odds)
: 로지스틱 회귀에서 성공 확률에 대한 로그 승산을 선형식으로 추정함.
성공 확률 P와 승산(odds). 타겟에 대한 실패 확률에 대한 성공 확률의 비율
- y가 단순 0과 1일 경우, 회귀식의 범위와 일치하지 않지만, 승산을 이용할 경우, y 값의 범위가 0부터 양의 무한대까지로 나타날 수 있음 (0 <= p <= 양의 무한대)
- 그러나 승산을 이용한 y 값은 범위가 음수가 될 수 없음. 그리고 그래프가 지수함수로 비대칭적으로 나타나기 때문에 이 승산에 로그를 취해준 값을 사용함.
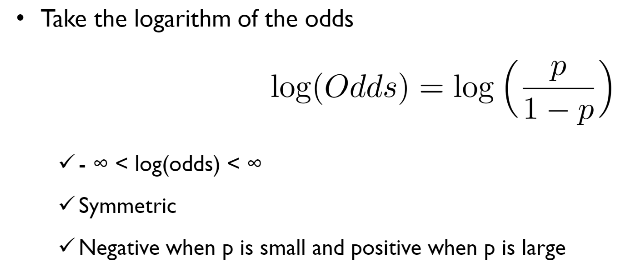log odds의 범위는 음의 무한대부터 양의 무한대로, 회귀식의 범위와 일치함. 그리고 대칭성 또한 존재함.
로지스틱 회귀 방정식과 성공 확률(P)에 대한 식
P : 사후확률에 대한 추정값
4. 로지스틱 회귀의 학습
- 선형 회귀의 회귀 계수는 closed form임(단순히 학습 데이터가 주어지고 그에 대응하는 종속 변수 값이 주어지면, 대단한 계산이 아닌 행렬 연산을 통해, 즉 모델의 학습 없이 해가 딱 떨어짐(discrete). 그러나 로지스틱 회귀의 회귀 계수는 그렇지 않음.
* 로지스틱 회귀의 학습 = 파라미터(w, 가중치)를 loss function의 value가 최소화 되는 방향(prediction - target 오차 줄이기)으로 업데이트하는 것.
선형 회귀 coefficient의 matrix form
4-1. 우도와 로그 우도
- likelihood(우도) : 모델이 정답을 맞출 확률(우도가 항상 P(y=1)을 뜻하는 건 아님. P(y=0)일 수도 있음. 즉, 타겟을 의미함).
- 전체 데이터셋에 대한 우도는 각 설명 변수(X1, X2, ...)의 우도를 모두 곱한 것임.
- 우도는 확률이므로 0과 1사이의 값을 가질 수 있는데, 이런 소수를 엄청 큰 데이터셋 전체에 곱해버리면(단, 곱하기 위해서는 각 설명 변수가 서로에 대해 독립적이어야 함) 숫자가 0에 수렴하려고 함.
- 전체 데이터셋에 대한 우도는 각 설명 변수(X1, X2, ...)의 우도를 모두 곱한 것임.
- log likelihood(로그 우도) : 이 문제를 해결하기 위해 나온 방식. 각 우도에 로그를 취한 것임.
- 그냥 우도보다 이것이 더 흔히 쓰임.
- 우도와 로그 우도는 클수록 좋음.
4-2. 최대 우도 추정법(Maximum likelihood estimation, MLE)
: 데이터셋의 우도를 최대화하는 회귀 계수를 찾는 방법
i번째 객체(설명 변수)의 우도를 찾는 식. 위의 식에서 yi = 1은 P(y=1)을 의미하는 것임. 아래 식은 P(y=0)일 때와 P(y=1)일 때의 우도를 한 번에 표현하는 식임
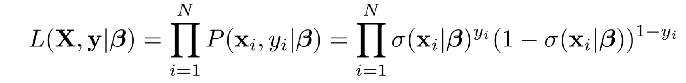데이터가 서로 독립적이라면, 전체 데이터셋의 우도는 위와 같이 표현됨 (저 기호는 product, 즉 모든 요소를 다 곱하는 걸 의미함.)
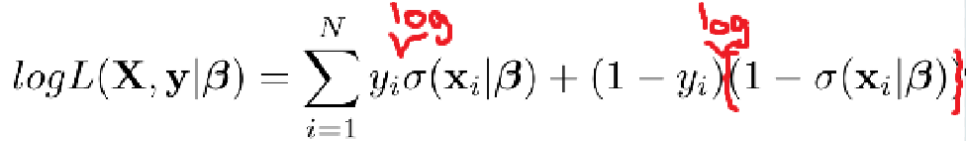그리고 로그 우도를 구하기 위해 양변에 로그를 취하면 위와 같음. (product에 로그 취하면 시그마가 됨) - 이 식을 maximize 해야 함!
* 우도는 베타에 대해 비선형적이므로, MLR(다중 선형 회귀)의 해(베타 혹은 웨이트)와 같이 해가 explicit하지는 않음.
-> MLE 및 Gradient Descent와 같은 최적화 알고리즘을 통해 해를 찾아야 함.
4-3. Gradient Descent(경사하강법)
: 오차(y - y hat, target-prediction)를 최소화하는 기법.
순서)
ㄱ. 초기화 : 모델의 파라미터(예, 가중치)를 무작위 값이나 특정 값으로 초기화
ㄴ. 그래디언트 계산 : 현재 파라미터에 대해 손실 함수의 그래디언트(미분 값) 계산
ㄷ. 파라미터 업데이트 : 그래디언트의 반대 방향으로 파라미터 조정함으로써 손실 함수의 값을 감소시킴 (learning rate라는 하이퍼 파라미터가 업데이트 크기를 결정함)
ㄹ. 수렴 체크 : 손실 함수의 값이 더 이상 감소하지 않거나, 미리 정한 기준에 도달할 때까지 위의 단계를 반복함.
- 이 때 하나의 설명 변수에 대한 가중치만 수렴시키는 게 아니라, 한 번에 모든 가중치들에 대한 업데이트가 이루어짐.
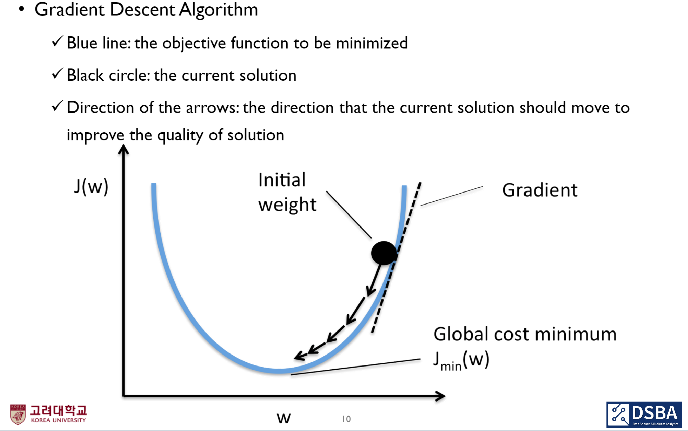J(w) : loss(cost) function. J(w)를 최소화하는 게 목표임.
- 첫 시작점(initial weight)은 무작위로 아무거나 하나 찍는 거라고 함.
- 해당 웨이트에 대한 cost function의 일차 도함수(웨이트에 대해 log(L) 미분)가 0이 될 때까지 계산을 계속 함.
- 일차 도함수가 0이 아니면, 일차 도함수의 반대 방향으로 웨이트를 옮김으로써 function value를 감소시킬 수 있음(아래 강의 화면 캡쳐본의 두번째 식)
- 학습을 계속 진행할 때 웨이트를 얼마나 옮겨야 하나?(=stepsize)
- 정해진 건 없음. 그냥 조금씩 옮겨야 함.
<Gradient descent 업데이트 방식>
w의 변화량이 충분히 작을 때, w에 대한 함수는 위와 같이 무한 급수로 표현될 수 있음(테일러 전개). 또한 w 변화량에 대한 이차항(위의 식에서 우변 세번째 항부터) 뒤로는 0으로 근사될 수 있음.
- 여기서 웨이트에 대한 함수 f(w)는 단순 식이 아닌 행렬(?)임.
- 우도 및 로그 우도는 클수록, 손실 함수는 작을수록 좋음.
- 기계 학습에서 '로그 우도의 음수'를 손실 함수로 사용할 수 있으며, 이를 최소화하는 것이 MLE와 같은 효과를 가짐. (예, 로지스틱 회귀에서 로그 우도를 최대화하는 것은 교차 엔트로피 손실 함수를 최소화하는 것과 같음) -> 우도와 손실 함수의 관계!!!!!
- '로그 우도의 음수'를 손실 함수로 사용하는 이유 : (로그)우도는 최대화하고 손실 함수는 최소화해야하는데, 손실 함수와 동일하게 (로그) 우도도 최소화시키면 편하니까
- loss(cost) function의 선택은 문제의 유형에 따라 달라짐 (예, 회귀 문제에서는 MSE, 로지스틱 회귀에서는 로그 우도의 음수(Negative log-likelihood, NLL), 분류 문제에서는 교차 엔트로피나 로그 손실(log loss)를 사용함)
- cross entropy와 log loss는 같은 걸 가리키는 말임. 둘 다 모델의 예측 확률 분포와 실제 레이블의 확률 분포 사이 차이를 측정하는 방법임
- 이진 분류 문제에서는 log loss, 다중 분류 문제에서는 cross entropy가 더 많이 쓰이는 말임
- 예측된 확률과 실제 레이블 간의 차이를 최소화하는 방향으로 모델을 조정하는 데 사용됨
<로지스틱 회귀 모델의 구조 정리>
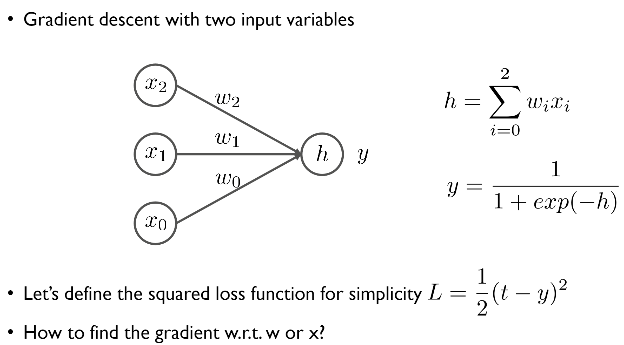
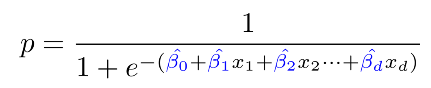분모의 괄호 안에 있는 식이 위의 그림에서 h를 뜻함.
h : 입력(설명 변수)x와 가중치 w(beta)의 선형 조합
y : 로지스틱 회귀 함수를 통해 계산된 모델의 예측값. (이는 h를 사용해 0과 1사이 값으로 변환됨)
L : 손실 함수 (예측값 y와 실제 타겟 t 간 제곱 차이) - 전에는 타겟은 y, 예측값은 y hat으로 나타냈었음. (여기서 손실 함수는 제곱 손실 함수임. 제곱 손실 함수는 선형 회귀에서 사용됨.)
** 선형 조합이란 ?
여러 벡터들에 스칼라곱을 하고 그 결과를 더하는 것 (선형식이라 해서 꼭 1차식인 건 아님.)
<그래디언트 계산과 파라미터 업데이트 과정>
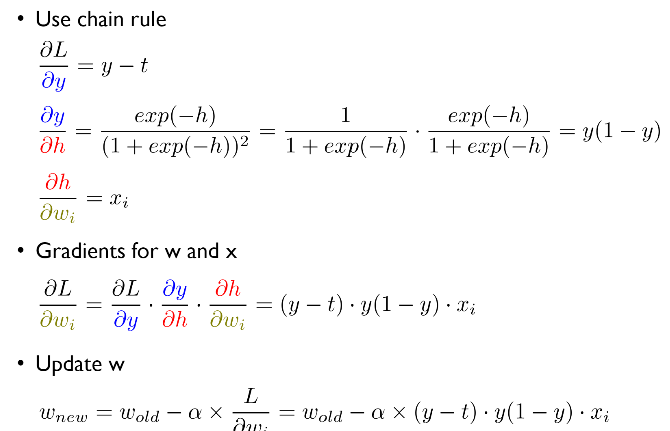여기서 alpha(learning rate) 설정에는 여러 의견이 분분함.
가중치 업데이트에 대한 추가 설명
- chain rule을 사용해 파라미터 w에 대한 손실 함수 L의 그래디언트(round L/round wi)를 계산한 후, w를 업데이트하기 위해 계산된 그래디언트를 현재 w에서 뺌 -> loss 최소화하는 파라미터 w를 찾기 위한 반복적인 접근법.
- (y-t) : 오차가 작으면, 학습이 어느정도 안정화되어있으므로 웨이트(미지수)를 덜 움직임. 차이가 클수록 더 많이, 빠르게 움직임.
- xi : 가중치를 업데이트하는데 있어서, 그 가중치와 연관있는 설명 변수의 값에만 영향을 줌.
- gradiet descent에 사용되는 loss function을 뭘로 정의하냐에 따라 위의 가중치 업데이트 식은 달라짐.
5. 로지스틱 회귀의 예측
: 로지스틱 회귀 모델의 학습 과정(가중치(파라미터, w0, w1..)를 최적화하여 데이터에 가장 잘 맞도록 조정됨)이 완료된 후, 새로운 데이터(설명 변수)에 대한 예측(성공 확률 p)을 수행하는 단계.
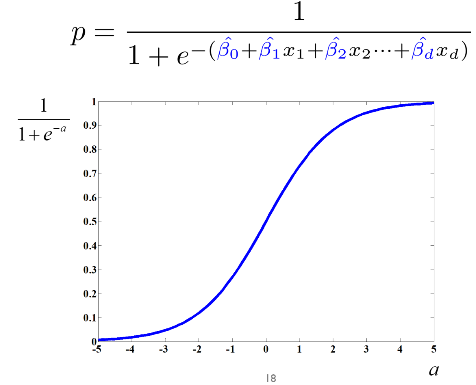
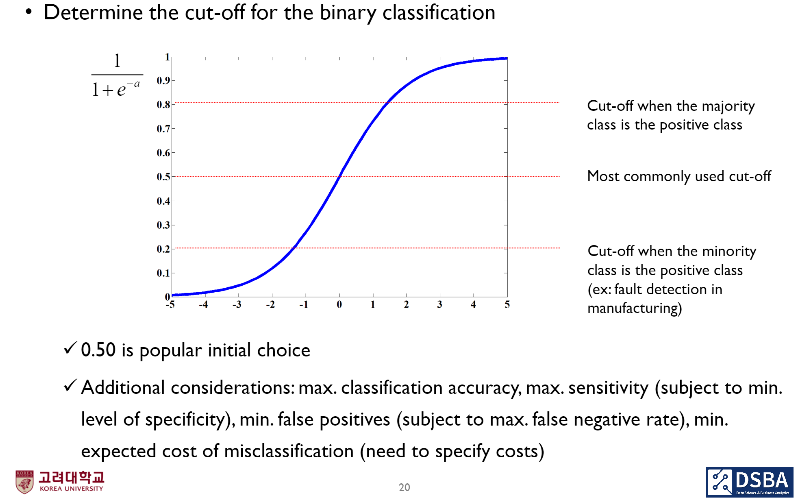
- 타겟에 대한 cut-off를 어떻게 설정하냐에 따라 분류의 결과가 매우 달라짐.
- 그래서 classfication accuracy, sensitivity, flase positive를 최대화, false positive, expected cost of misclassification 등 다양한 요소들을 고려해 임계값을 조정해야 함.
- 문제의 맥락에 따라 임계값이 달라질 수 있음(결함 감지와 같이 소수 클래스가 양성인 제조 분야에서는 보다 낮은 임계값을 설정해야 함)
6. 로지스틱 회귀 모델 결과의 해석
: p value, coefficients, odd ratio 종합해서 결과를 봐야
-
선형 회귀는 X1가 1만큼 커지면 Y hat은 b1만큼 커짐. 이렇게 직관적인 결과를 보여주는데 로지스틱 회귀는 그렇지 않음.
-
로지스틱 회귀의 주요 해석 도구 : 오즈 비(odd ratio)
: 설명 변수가 1만큼 증가하면, 승산 비율이 얼마나 증가하는가? (선형 회귀처럼 특정 설명 변수의 영향력을 직관적으로 해석하기 위한 것)
-
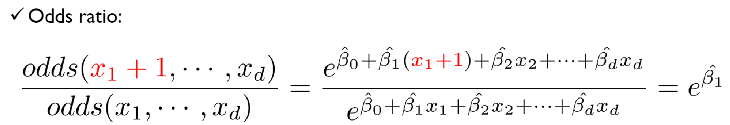
선형 회귀의 해석과 유사하게, 하나의 설명 변수(x1) 값이 한 단위 증가할 때, 다른 변수들의 값이 고정된 상태에서, 성공의 odds가 어떻게 변화하는지를 나타내는 비율.
- b1 > 0 : x1이 한 단위 증가하면, 성공의 odds는 e^b1배 증가함 (설명 변수와 성공 확률이 양의 상관 관계를 갖고 있음)
- b > 0 ~~ e^b1 > 1 ~~ odd ratio 증가 = P 증가
- b1 < 0 : x1이 한 단위 증가하면, 성공의 odds는 e^b1배 감소함 (설명 변수와 성공 확률이 음의 상관 관계를 갖고 있음)
- b < 0 ~~ e^b1 < 1 ~~ odd ratio 감소 = P 감소
- odds ratio > 0 : coefficient > 0
- odds ratio < 0 : coefficient < 0
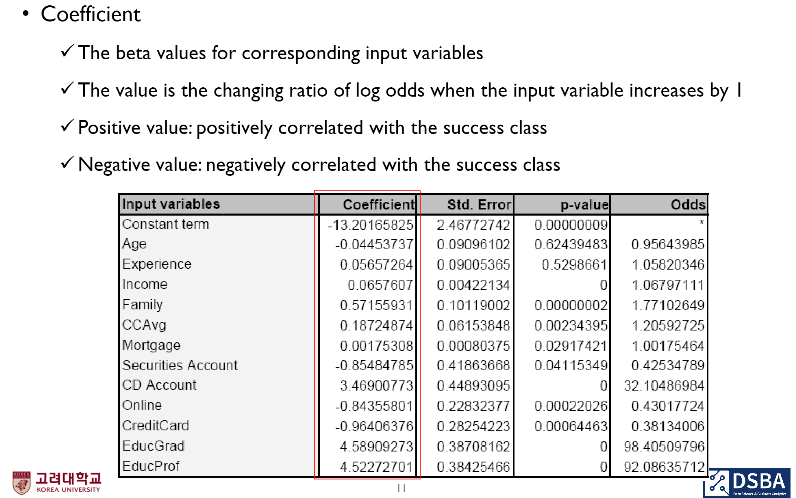
- b1 > 0 : x1이 한 단위 증가하면, 성공의 odds는 e^b1배 증가함 (설명 변수와 성공 확률이 양의 상관 관계를 갖고 있음)
7. Multinomial Logistic Regression (타겟이 여러 종류 = 다변량)
: 타겟 y의 종류가 3가지 이상일 때(0,1의 두 가지가 아니라 여러개일 때), baseline을 설정해야 함. 그리고 baseline class와 비교 class끼리 relative log odds에 대한 회귀식을 형성해야함.
다변량 로지스틱 회귀에 k개의 클래스(범주)가 있으면, (k-1)개의 모델을 생성해서 풀 수 있음.
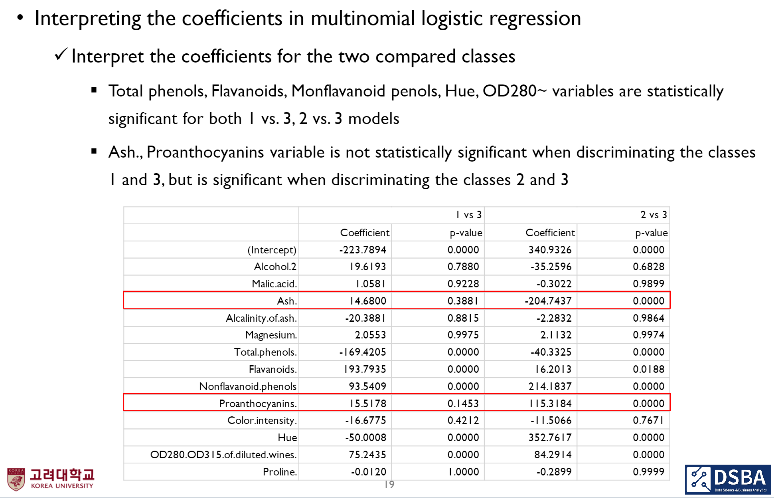로지스틱 다항 회귀 분석에서, 각각의 변수가 특정 두 범주 구분에 대한 판별력은 떨어질 수 있어도, 다른 범주 구분에 대한 판별력을 줄 수 있음.
8. 분류 모델의 평가 지표 (로지스틱 회귀뿐만 아니라 다른 분류 모델에도 사용됨)
최적의 모델 찾는 방법
1) 각 알고리즘별 베스트 하이퍼 파라미터 조합 찾기 (validation set 사용)
예) k means neighbor - k(3), classification tree - minimum split(10), NN - hidden node(10) 등
2) 그 알고리즘별 베스트 하이퍼 파라미터 조합들 중 가장 나은 알고리즘 고르기 (test set 사용)
예) classification tree가 가장 낫다.
-
단순 정확도
BFP 기준으로 성별을 맞춘 케이스는 7/10*100 = 70% (단순 정확도)
-
Confusion Matrix (예시는 위의 단순 정확도에 대한 것)
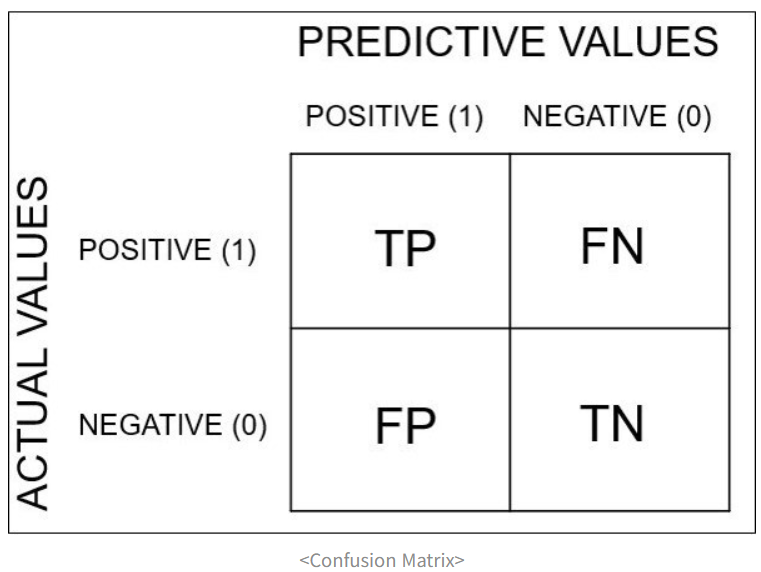
confusion matrix로 계산할 수 있는 '분류' 모델 성능 평가 지표 (measures)
1) Misclassification error : 전체 중 모델이 틀리게 분류한 비율
= (FN+FP) / (TP+FN+FP+TN)
2) Accuracy : 전체 중 모델이 바르게 분류(대각 행렬)한 비율
= (TP+TN) / (TP+FN+FP+TN) = 1-misclassification error
3) Recall : 진짜 불량 제품을 얼마나 잘 걸렀는가 (실제 False 중 모델이 False라고 예측한 비율)
4) Precision : 모델이 불량이라고 예측한 것 중, 실제 불량이 몇 개인가 (모델이 False라고 예측한 것들 중 진짜 False)
5) Balanced correction rate(BCR) : root{ (실제 True 중 모델이 True라고 예측한 것의 비율) (실제 False 중 모델이 False라고 예측한 것의 비율) }
6) F1 score : (2Recall*Precision) / (Recall+Precision) = Recall과 Precision의 기하평균
-> BCR과 F1 score를 많이 씀
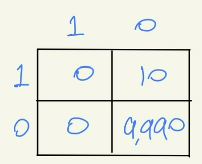단순 Accuracy의 단점 : 0.999 acc이라고 해도 해당 모델이 정확하다고는 말할 수 없음.
confusion matrix와 cut-off의 종속 관계
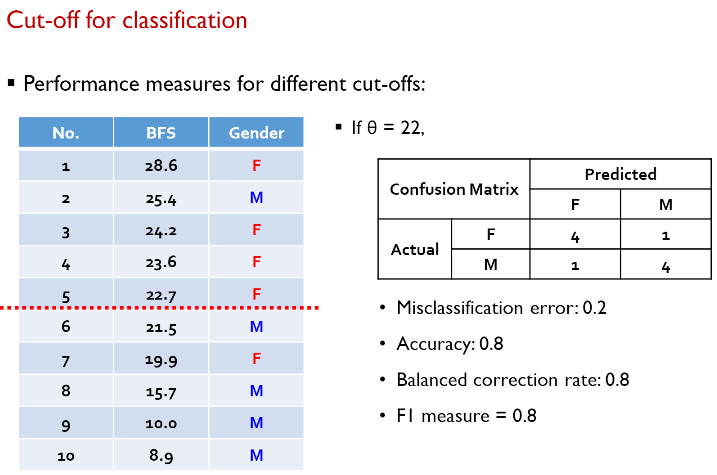
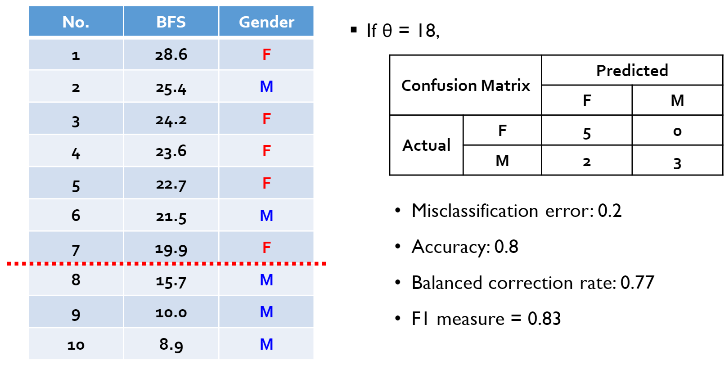
- 위의 '분류' 성능 평가 지표들은 confusion matrix때문에 cut-off의 영향을 크게 받는다. (cut-off가 달라지면 성능 평가 지표들도 달라짐)
- 모델의 퍼포먼스가 cut-off에 따라 달라진다면 본질적인 퍼포먼스를 측정하는 다른 방법은? ROC(Receiver Operating Characteristic) curve
- 100개의 레코드(데이터)를 우리가 원하는 범주에 대한 확률값(P(NG))에 대해 내림차순한다.
- 각각의 Case(조합)에 대해 True Positive Rate(TPR-정답 확률)와 False Positive Rate(FPR-오답 확률) 각각에 대해서 다 계산을 해본다.
- 그 경우, 가능한 cut-off의 개수는 총 101가지가 된다.
ROC example
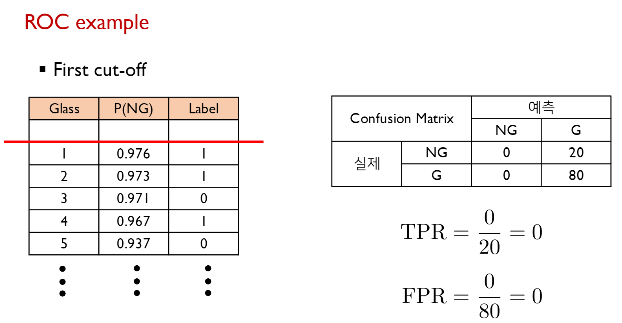
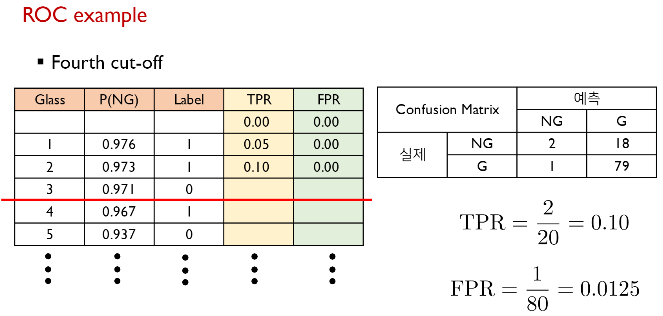cut-off를 아래로 내릴수록 TPR과 FPR이 높아짐.
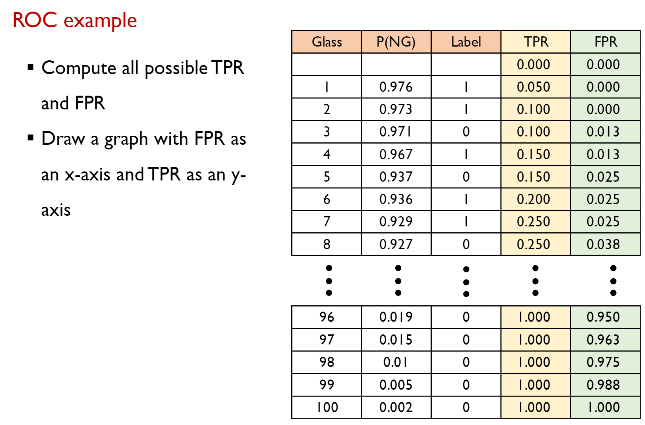모든 cut-off에 대해 각각 TPR과 FPR을 계산한 예시
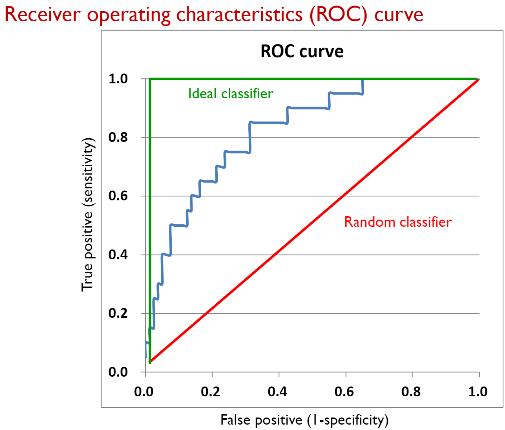FPR(x), TPR(y)의 비율
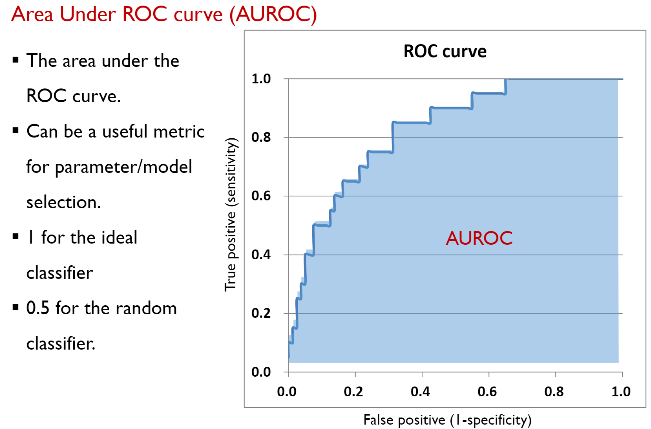ROC를 수치로 나타내기 위한 AUROC (ROC 밑면 넓이)
*이런 알고리즘들의 기하학적 정의(매트릭스로의 정의 - 선형대수학)를 추가적으로 이해해야 함
