🐼 목 차 🐼
1. 시계열 분석이란?
2. 시계열 데이터란?
3. 시계열 데이터의 구성 요소
4. 시계열 분석의 목적
5. 시계열 분석 시 주의해야 할 점들
6. 시계열 분석 기법
7. 시계열 분해(Timeseries Decomposition)
1. 시계열 분석이란?
- 시간에 따라 연속적으로 발생하는 데이터를 분석하고 예측하는 방법론
- 시간의 흐름에 따라 데이터가 어떻게 변화하는지 이해하고, 과거 데이터를 기반으로 미래의 값을 예측하는 데 사용됨
2. 시계열 데이터란?
- 일정한 시간 간격으로 측정된 데이터로 구성됨 (예, 일일 주식 가격, 매월 판매량, 시간당 온도 등)
- 이러한 데이터는 시간의 흐름에 따라 패턴, 계절성, 추세 등을 나타내는 경향이 있음
- 일반적으로
진동수 도메인과시간 도메인으로 나뉨진동수 도메인: 신호처리 분야에서 주로 사용. 진동수의 노이즈를 제거하는 방법에 관심을 가짐.시간 도메인: 일반적으로 시계열 데이터는 일정하고 이산적인 시간 간격을 전제로 하고 있고, 그 경우 시간 도메인이 주로 이용됨- 시간 도메인 영역에서는 시계열 데이터를 하나의 연속된 배열(시퀀스)로 보기도 하며, 이런 시퀀스 기반 분석이 가장 많이 활용되는 분야가 GPT, BERT와 같은 자연어처리(NLP) 분야임
3. 시계열 데이터의 구성요소
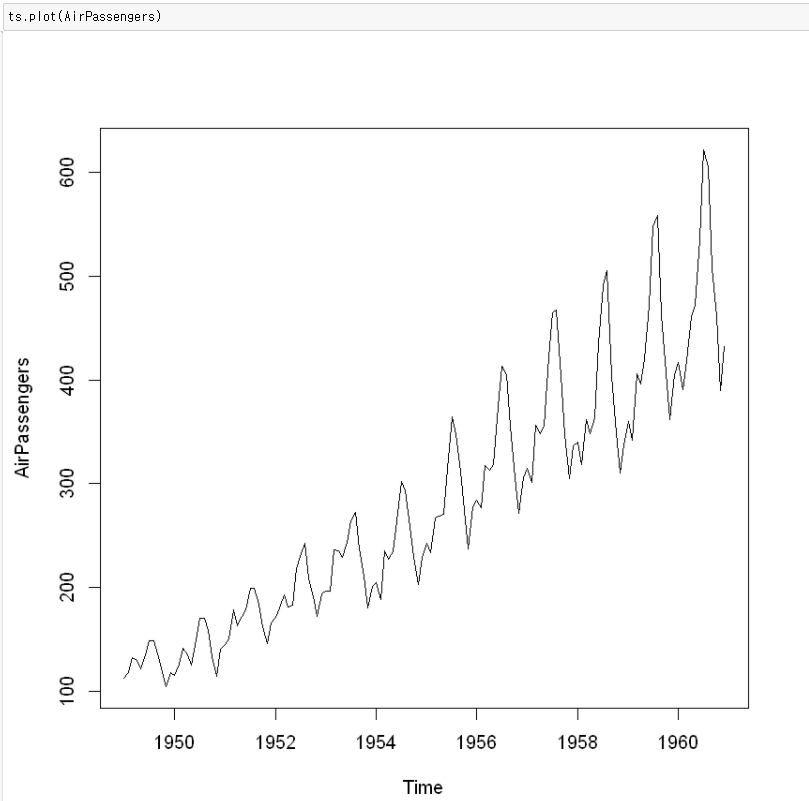
- 추세(Trend) : 데이터가 장기적으로 증감하는 경향성 (꼭 선형적일 필요 X)
- 시계열 데이터의 전반적인 경향을 파악하는 데 도움을 줌
- 위의 데이터는 증가하는 경향을 보이고 있음
- 계절성(Seaonality) : 데이터가 일정한 기간(연도, 분기, 월 등)에 따라 반복되는 패턴을 보이는 것
- 주기적인 변동을 파악해 향후 예측에 활용할 수 있음
- 위의 데이터는 월별 주기로 등락을 거듭하는 경향이 나타남
- 주기성(Cyclicity) : 데이터가 일정하지 않은, 장기적인 주기로 변동하는 패턴을 보이는 것
- 긴 주기나 불규칙한 주기를 가질 수 있음
- 주기성은 장기적인 패턴을 파악해 경향성을 이해하는 데 도움을 줌
- 불규칙 요소(Random, Residual) : 설명될 수 없는 요인 또는 돌발적인 요인에 의해 발생하는 변화 (예측불가능한 임의의 변동)
- 아래에서 설명할 분해법에서는 원래 데이터에서 trend, seasonality, cyclicity를 제외한 나머지를 불규칙 요소라고 함
- 아래에서 설명할 분해법에서는 원래 데이터에서 trend, seasonality, cyclicity를 제외한 나머지를 불규칙 요소라고 함
※ 빈도가 변하지 않고 연중 특정 시기와 연관되어 있는 경우는 'Seasonality'을 나타냄
※ 주기들의 평균 길이는 계절성 패턴의 길이보다 길고, 주기의 크기는 계절적 패턴의 크기보다 좀 더 변동성이 큰 경향이 있음
※ 한편, 주기성은 학자마다 정의가 약간씩 다르다고 함!
- 시계열 데이터의 형태
- 계절 변동
- 추세 변동
- 계절적 추세 변동
- 순환 변동
- 우연 변동(=White noise)
⭐ 백색 잡음(White Noise)
-
패턴이 존재하지 않고 무작위로 발생하는 잡음
- 시계열 데이터를 전처리한다는 것은, 다른 패턴을 다 배제한 후 백색 잡음을 얻어내는 것을 의미함. 이 백색 잡음을 통해 시계열 데이터 분석 및 예측을 수행할 수 있음.
-
백색 잡음은 다음의 두 가지 속성을 만족해야 하고, 하나라도 만족하지 않으면 모델을 개선시켜야 함
- 잔차들은 평균, 분산, 자기공분산이 일정해야한다.
- 잔차들이 시간의 흐름에 따라 상관성이 없어야 한다. (=자기상관성)
- 잔차가 위의 조건을 만족하면서 정규분포를 따를 경우, 이를 가우시안 백색 잡음 이라고 함
- 각 데이터가 각각 독립성을 갖는 것은 시계열 데이터의 기본적인 가정이기도 하고, 이를 i.i.d.라고도 부름 (individually and independently distributed)
- 이러한 상관성은 ACF, PACF 등과 같은 함수들을 통해 확인해볼 수 있음 (후술)
-
시계열 예측 모델이 실제 현상의 트렌드와 주기를 잘 반영할수록 잔차의 변동이 줄어들고, 이를 바탕으로 모델이 개선되었는지 여부를 파악할 수 있음 (by 시각화)
-
정상성뿐만 아니라, 정규성, 자기상관성, 등분산성 또한 잔차 진단에 적용되며, 이 특성들을 시계열 데이터 모델의 기본 가정 이라고 함
| 정상성 | 정규성 | 자기상관성 | 등분산성 | |
|---|---|---|---|---|
| 대표적인 검정 | ADF, KPSS | Shapiro-Wilk, Kolmogorov-Smirnov test | Ljung-Box test, Prtmanteau test | Goldfeld-Quandt test, Breusch-Pagan test |
| 귀무가설 | ADF : 단위근이 존재함 (비정상) KPSS : 단위근이 존재하지 않음 (정상) | 정규분포를 따름 | 시간이 지나면 자기상관성은 0임 | 시간이 지나면 등분산임 |
4. 시계열 분석의 목적
- 데이터의 패턴 및 구조 파악 : 시계열 데이터를 분석해 주기성, 계절성, 추세 등과 같은 패턴이나 구조를 파악함
- 예측 및 추론 : 과거 데이터를 기반으로 미래의 값을 예측하고 추론하는 데 사용됨 (수요 예측, 주가 예측, 날씨 예측)
- 이상 탐지 : 시계열 데이터에서 이상치나 비정상적인 동작을 탐지하는 데 사용됨 (특이한 패턴이나 이상한 동향을 감지해 문제 및 오류 식별)
5. 시계열 분석 시 주의해야 할 점들
- 자기상관(autocorrelation)에서 자유로울 수 없어, 데이터 간 연관성을 고려해야함
- 자기상관 : 어떤 확률 변수가 주어졌을 때, 서로 다른 두 시점에서의 관측치 사이에 나타나는 상관성
- 시계열 모델링의 기본은 현재 데이터를 설명하는 데 있어, 과거 데이터를 얼마나 활용하는지에 따라 달라질 수 있음 (딥러닝 장단기 기억모형에서 중요한 개념)
- 결측치가 많거나 불균형한 빈약한 자료를 다룰 때 더 주의해야함
- 예측을 실시해 추정치를 얻는 경우, 수리적 통계모형에 의한 인과관계와 시간의 상관관계를 고려해 미래 시점의 추정치를 얻어야함
6. 시계열 분석 기법
- 시계열 데이터의 처리
데이터의 잡음이나 변동성을 제거하고, 패턴(trend, seasonality 등)을 부드럽게 만들어서, 패턴 파악을 용이하게 만드는 기법들
-
시계열 분해
- 내재된 변동 요인이 고정적인 패턴을 보이는 경우
- 가법 모형(덧셈 분해), 승법 모형(곱셈 분해) - 아래에 서술
-
평활법(Smoothing)
- 다양한 변동 요인이 고정적인 패턴을 보이지 않는 경우
- 이동평균 평활법(MA Smoothing)
- 일정 기간 내의 데이터를 평균해 부드러운 추세를 갖게 하는 것
- 지수평균 평활법(Exponential Smoothing)
- 모든 데이터를 평균하고, 시간의 흐름에 따라 최근 데이터에 더 많은 가중치를 부여함
-
log 변환
- 변동폭이 일정하지 않은 경우
-
차분(Differencing)
- 추세, 계절성이 존재하는 경우
- 추세, 계절성이 존재하는 경우
-
시계열 예측 모델
- 통계적 기법
- AR, MA, ARMA, ARIMA 등 → 단변량
- 자기상관성, 계절성, 추세 등을 고려하여 예측 수행
- 머신러닝
- 회귀 분석, 의사결정트리, 랜덤 포레스트, SVM 등의 알고리즘
- 과거 데이터의 패턴을 학습하고 이를 기반으로 미래값을 예측
- 딥러닝
- RNN, LSTM
- 긴 시퀀스 데이터의 의존 관계를 모델링해 예측 성능 향상
- 통계적 기법
7. 시계열 분해(Timeseries Decomposition)
-
위와 같은 속성들을 분리해내는 과정
-
이를 통해 데이터의 구성 요소를 분리해 각각의 영향을 파악할 수 있음
덧셈 분해(Additive Decomposition) :
Yt = Tt(추세) + St(계절성) + Ct(주기성) + Rt(잔차)곱셈 분해(Multiplicative Decomposition) :
Yt = Tt(추세) St(계절성) Ct(주기성) * Rt(잔차) -
Additive vs Multiplicative
- 덧셈 분해는 데이터가 선형적이고, trend, seasonality, ciclicity가 서로 독립적이라고 가정할 수 있는 경우에 사용
- 곱셈 분해는 데이터가 비선형적이고, trend, seasonality, ciclicity가 서로 영향을 주고 받는 경우에 이용
- 아래의 예시에서 좌측은 시간이 지남에 따라(trend가 변함에 따라) 변동폭이 일정하지만, 우측은 trend가 상승함에 따라 변동폭 또한 증가하고 있음
- 따라서 좌측 예시는 additive가 적절하고, 우측 예시는 multiplicative가 적절함
좌-additive, 우-multiplicative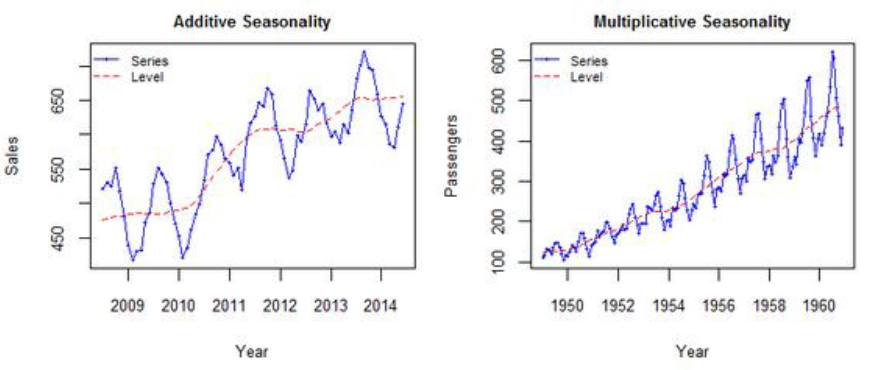
-
시계열 분해와 ARIMA
- 시계열 분해는 ARIMA 모델의 전처리 과정으로 사용될 수 있음
- 시계열 분해를 통해 trend 및 seasonality를 분리한 후, ARIMA 모델에 residual 부분을 적용해, residual의 자기회귀 및 이동평균 성질을 모델링할 수 있음
8. 정상성(Stationarity)
정상성 = 시계열의 통계적 특성이 시간에 따라 일정하게 유지되는 성질 (일정, 한결같은 성질)
- 정상성(Stationarity)은 시계열 분석 시 필수적으로 고려해야하는 가정임
- 정상성을 만족해야 분석 결과에 대해 신뢰할 수 있음
Q) 그럼 어떤 시계열이 정상성을 갖는 시계열이냐?
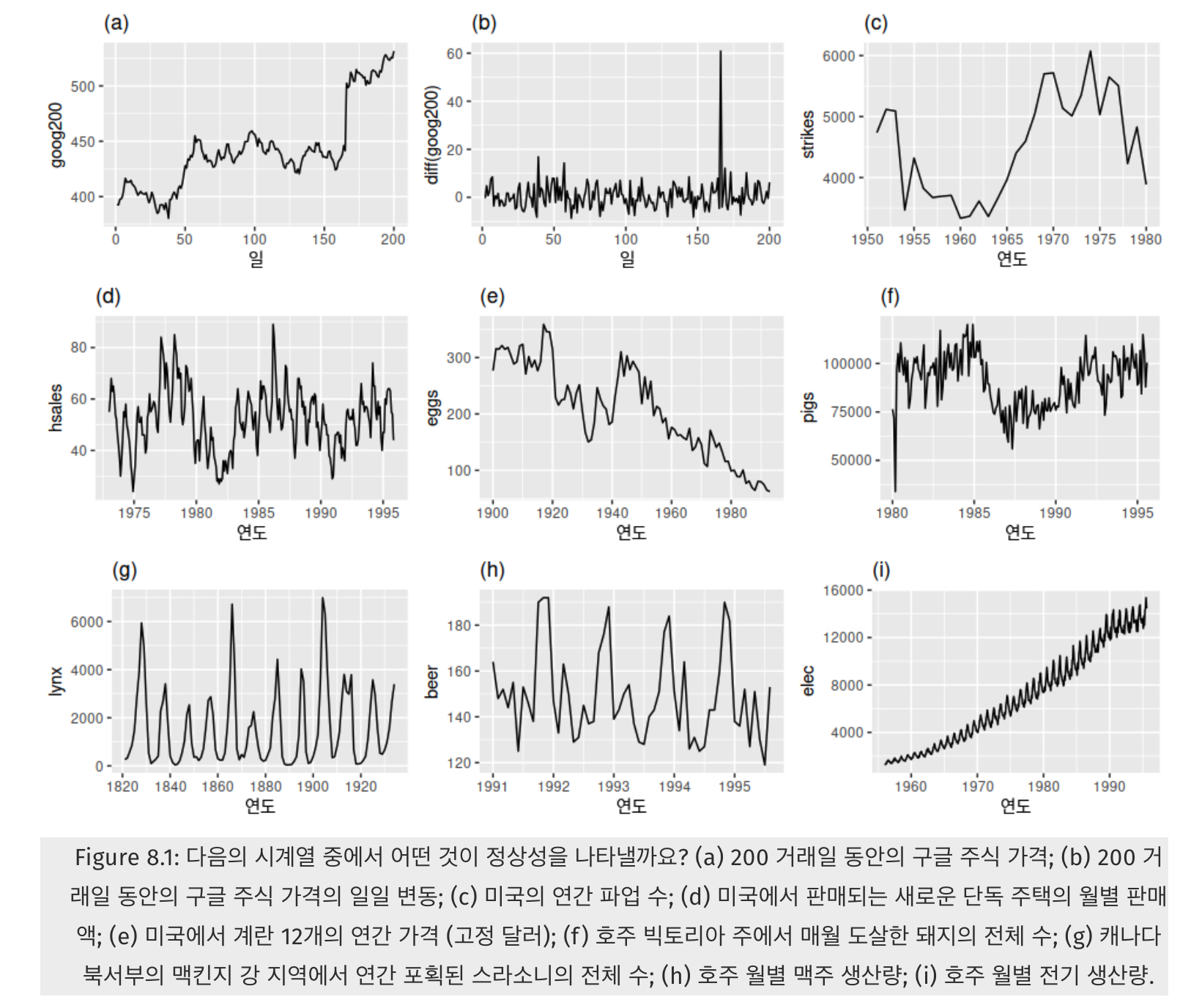
(d), (h) : seasonality가 보여 정상성을 띄지 않음
(a), (c), (e), (f) : trend가 보여 정상성을 띄지 않음
(i) : trend, seasonality가 보이고, 분산도 시간에 따라 커지는 형태이므로 정상성을 띄지 않음
-
정상성을 만족하려면 trend나 seasonality, ciclicity가 없어야 하고, 분산도 변하면 안 될 거라 유추할 수 있음
- 즉, 시간에 무관하게 평균과 분산이 일정해야 함
- 즉, 시간에 무관하게 평균과 분산이 일정해야 함
-
강한 정상성(Strong Stationarity)과 약한 정상성(Weak Stationarity)
- 강한 정상성을 만족하는 시계열은 대부분 약한 정상성을 만족하므로(cf, idd Cauchy 분포 등), 약한 정상성만 알아보자
- 약한 정상성 : 어느 시점에 관측해도 확률 과정의 성질이 변하지 않는다.
✔️ 약한 정상성을 위한 세 가지 조건
1. 시점 ( t )에 대해서
: 데이터 X가 시간에 따라 변하지 않는 평균을 가짐
2. 시점 ( t )에 대해서
: 데이터 X의 분산이 무한대가 아님 (데이터 변동성이 무한히 커지지 않고 특정 범위 내에 제한됨)
3. 시점 ( t, h )에 대해서
: 데이터의 공분산이 두 시점 간의 시차에 의존하며,
특정 시간에 의존하지는 않음 (데이터가 시간의 흐름에 따라 일정한 자기상관 구조를 갖음)
-
정상성은 왜 중요한가?
- 데이터가 일정한 평균과 분산을 가진 확률 과정(stochastic process)을 따른다고 가정해야 시계열 예측을 수행할 수 있음
- 확률 과정 : 시간별로 표시된 확률 변수의 집합
- 정상성을 갖지 않은 시계열 데이터는 시간의 흐름에 따라 평균과 분산이 변하고, 그래서 데이터의 패턴을 파악하기 어렵게 됨 (overfitting 가능성 ↑)
※ 후에 다룰 ARIMA 모델의 경우, 이 정상성을 만족함을 가정으로 한다.
- 데이터가 일정한 평균과 분산을 가진 확률 과정(stochastic process)을 따른다고 가정해야 시계열 예측을 수행할 수 있음
-
정상성 만족 여부 판별을 위한 검정
- 통계 기법
- ADF(Augmented Dickey-Fuller) 검정
- KPSS(Kwiatkowski-Phillips-Schmidt-Shin) 검정
- 그래프로 확인하는 기법
- ACF(Auto Correlation Function)
- ACF(Auto Correlation Function)
- 통계 기법
-
정상성을 만족시키기 위한 방법들
- LOESS(Local regression, 회귀)
- 평활법(smoothing)
- 시계열 분해는 평활법을 활용함
- 이동평균 평활법(Moving Average Smoothing), 지수 평활법(Exponential Smoothing), OLS(회귀 모형 평활법) 등
- LOESS나 평활법을 활용해, 시계열 요소(trend, seasonality)를 추정하고 이를 제거함
- 차분(Differencing)
- 추세, 계절성이 존재하는 경우
- 평균을 일정하게 함
Yt - Yt-1- 1차 차분, 2차 차분, 역차분, 계절성 차분 등
- 로그 변환(Log Transformation)
- 변동 폭이 일정하지 않거나, 값의 변동 자체가 큰 경우(=분산이 큰 경우) 고려하는 방법 (예, 지수적 성장을 보이는 데이터)
- 변동폭(분산)을 일정하게 함
- 로그 차분(로그 변환 + 차분)
- 로그 변환을 해도 데이터에 트렌드가 보이는 경우 사용
- 로그 변환을 통해 데이터의 분산 안정화+선형화, 차분 통해 정상성 만족 (일정한 평균과 분산 만들기)
- 시계열이 선형적이라는 것 = 시간에 따른 증가율(차분)이 일정함
- 로그의 차분값 = 증가율의 근사값
GDP의 증가율이 AR(1) 과정을 따릅니다.→ 좀 더 직관적으로 이해가능한 분석
- ACF/PACF(자기상관함수)
- ARIMA 모델의 차수를 결정하고 정상성을 만족시키는데 도움을 얻을 수 있음
- ARIMA 모델의 차수를 결정하고 정상성을 만족시키는데 도움을 얻을 수 있음
