시계열) RNN

Joo·2024년 3월 22일
RNNTimeseries
0

Data Analytics 101

목록 보기
6/15

🐼 목 차 🐼
1. 시계열 데이터(Time series data)
2. 시계열 데이터 분석 방법론 트렌드
3. 다른 시계열 모델과 RNN
4. RNN 한계점

참고 강의 링크 : https://www.youtube.com/watch?v=006BjyZicCo&list=PLpIPLT0Pf7IoTxTCi2MEQ94MZnHaxrP0j&index=3


1. 시계열 데이터(Time series data)

  • 시간의 흐름에 따라 관측되어 시간의 영향을 받게 되는 데이터
  • 현재 상태가 과거의 상태에 영향을 받음


2. 시계열 데이터 분석 방법론 트렌드

✔️ 전통 통계 기반 시계열 데이터 분석 방법론

  • 이동평균법 (Moving average
  • 지수평활법 (Exponential smoothing)
  • ARIMA (Autoregressive integrated moving average) 모델
  • SARIMA (Seasonal ARIMA) 모델
  • Binary variable model (해당 시점만 1, 나머지는 0으로 변환)
  • Trigonometric model (sine과 cosine 함수의 조합으로 표현)
  • Growth curve model
  • ARIMAX (Autoregressive integrated moving average exogenous)
    • X변수를 이용하여 시계열 Y 예측
  • Prophet, ...

✔️ 머신러닝 기반 시계열 데이터 분석 방법론

  • Linear regression/Logistic regression models
  • SVM/regression
  • Random forest
  • Boosting
    • 앞의 네 가지는 실제 시계열 특화는 아니지만 데이터를 약간 변형해서 사용 가능함
  • Hidden Markov model (HMM)

✔️ 인공지능 기반 시계열 데이터 분석 방법론

  • RNN (Recurrent neural networks, 1986)
  • LSTM (1997)
  • GRU (2014)
  • Seq2Seq (NIPS 2014)
  • Seq2Seq with attention (ICLR 2015)
  • CNN (Convolution neural networks) for time series analysis (2016)
  • Transformer (NIPS 2017)
  • GPT-1 (2018), BERT (2019), GPT-3 (2020), GPT-3.5 (2022), ChatGPT (2023) → 거대 언어 모델
    • GPT의 'T'는 트랜스포머를 의미함

3. 다른 시계열 모델과 RNN

1) 선형 회귀 모델

f(X)=w0+w1X1+w2X2f(X) = w_0 + w_1X_1 + w_2X_2

  • 로지스틱 회귀 모델의 베이스

2) 로지스틱 회귀 모델

f(X)=11+e−(w0+w1X1+w2X2)f(X) = \frac{1}{1 + e^{-(w_0 + w_1X_1 + w_2X_2)}}

  • NN 모델의 베이스
  • X들의 선형 결합 결과를 시그모이드 함수를 이용해 비선형 변환을 수행해 0-1 사이 확률값으로 변환

3) 뉴럴 네트워크 모델과 RNN

f(X)=11+exp⁡(−(z01+z1111+exp⁡(−(w01+w11X1+w12X2))+z2111+exp⁡(−(w02+w12X1+w22X2))))f(X) = \frac{1}{1 + \exp\left( -\left( z_{01} + z_{11} \frac{1}{1 + \exp(-\left( w_{01} + w_{11}X_1 + w_{12}X_2 \right))} + z_{21} \frac{1}{1 + \exp(-\left( w_{02} + w_{12}X_1 + w_{22}X_2 \right))} \right) \right)}
  • 로지스틱 회귀 모델을 여러번 결합한 것
  • RNN에서 Hidden vector를 구할 때 사용하는 함수 f : tanh activation function
  • RNN에서 최종 분류 문제를 풀 때 사용하는 함수 g : softmax function
  • 시계열 예측에서 DNN을 사용하지 않는 이유
    • DNN은 각 데이터가 서로에 독립적인 경우에 사용됨
    • 그러나 시계열 데이터는 각 시점의 데이터가 서로에 독립적이지 않아, 이전 시점 정보를 반영해야하기 때문
    • 이전 시점 데이터를 반영해서 더 나은 예측을 하자! → RNN 등장
  • 특정 시점 데이터에 이전 시점 데이터를 반영하는 법
    • 이전 시점의 hidden vector를 특정 시점의 hidden vector에 합성
    • 그 이전 시점의 hidden vector에는 더 이전 시점들의 vector 또한 반영되어 있음
ht−1=f(Wxhxt−1+Whhht−2)ht=f(Wxhxt+Whhht−1)yt=g(Whyht)where f(⋅)=tanh⁡, g(⋅)=softmaxh_{t-1} = f(W_{xh}x_{t-1} + W_{hh}h_{t-2}) \\ h_t = f(W_{xh}x_t + W_{hh}h_{t-1}) \\ y_t = g(W_{hy}h_t) \\ \text{where } f(\cdot) = \tanh, \, g(\cdot) = \text{softmax}
  • ⭐ RNN에서 학습(추정)해야하는 파라미터 세 가지
    • Why
      • 해당 시점에서의 hidden vector를 해당 시점에서의 y값으로 변환하는 파라미터
    • Wxh
      • 해당 시점에서의 관측치를 해당 시점에서의 hidden vector로 변환하는 파라미터
    • Whh
      • 이전 시점에서의 hidden vector를 현 시점의 hidden vector로 이동할 때 사용되는 파라미터
  • RNN의 파라미터는 시점에 관계없이 종류가 같으면 파라미터 값도 동일함 (parameter sharing)
    • 예, Whh는 시점에 관계없이 값이 다 같음

4) RNN 구조 다양성

  • RNN 구조의 종류

    • 순차적으로 입력하고, 순차적으로 예측하는 것이 가능
    • 순차적인 입력의 길이, 순차적인 예측의 길이에 따라 다음과 같이 분류됨

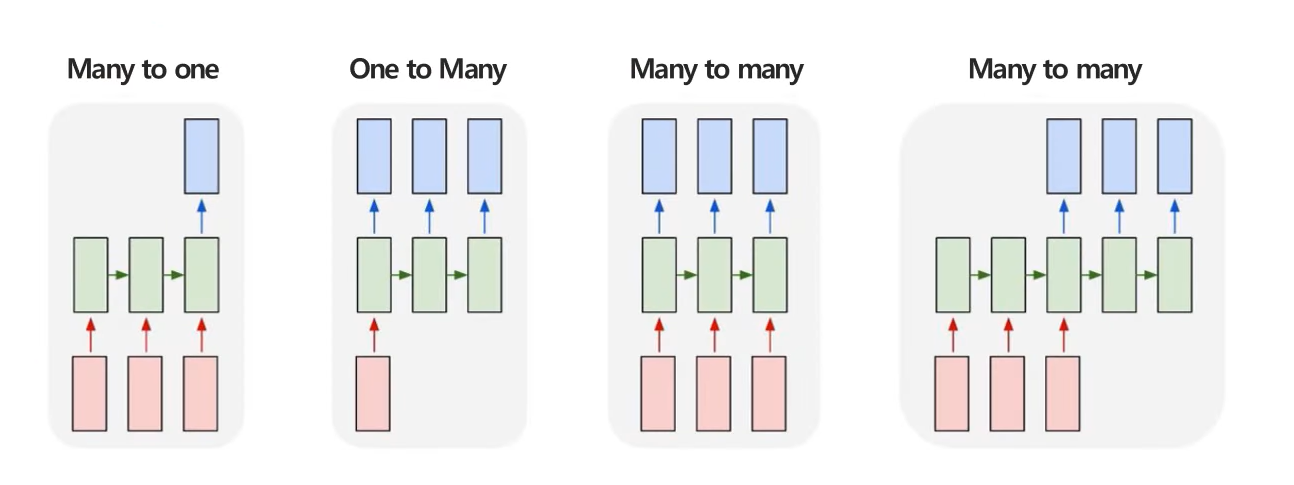
  • Many to one 구조

    • 여러 시점 X로 하나의 Y를 예측하는 문제
    • 예, 여러 시점에 다변량 센서 데이터가 주어졌을 때 특정 시점의 제품 상태를 예측

  • One to many 구조

    • 단일 시점 X로 순차적인 Y를 예측하는 문제
    • 예, 이미지 데이터가 주어졌을 때, 이미지에 대한 정보를 글로 생성하는 이미지 캡셔닝

  • Many to many 구조

    • 순차적인 X로 순차적인 Y를 예측하는 문제
    • 예, 문장이 주어졌을 때, 각 단어의 품사를 예측하는 POS Tagging

  • Many to many 구조 (many to one + one to many)

    • 순차적인 X로 순차적인 Y를 예측하는 문제 (Seq2Seq)
    • 예, 영어 문장이 주어졌을 때, 한글 문장으로 번역 (translation)
      • 입력된 문장을 요약해 요약벡터 생성(encoder)
      • 요약 벡터를 기반으로 출력 단어들을 예측(decoder)

5) RNN 학습

  • RNN은 t 시점까지의 (과거)정보를 활용하여 yt 예측
    • t 시점 데이터 반영 → Wxh
    • t 시점 이전 정보 반영 → Whh
    • t 시점의 y를 예측 → Why
  • 학습 대상(parameters) : (Wxh, Whh, Why)
    • 해당 파라미터는 매 시점마다 공유하는 구조
    • 매 시점 파라미터를 구성하는 값이 같음
    • 최적의 W : W를 매 시점 적용했을 때 Loss가 최소가 되도록

⭐ RNN 학습 과정

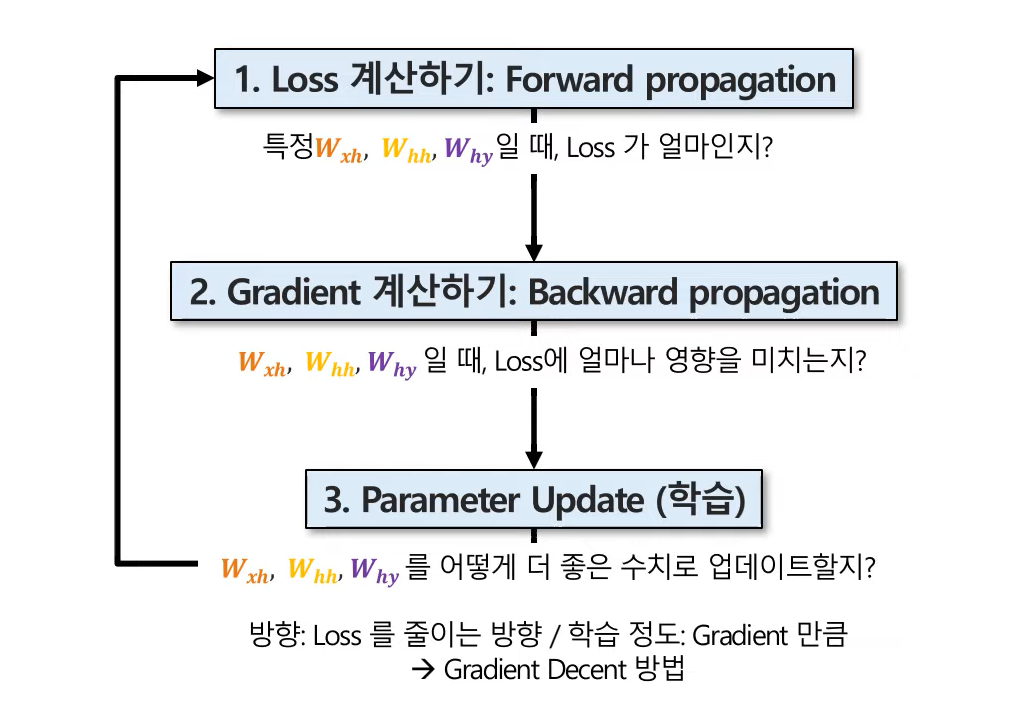
✔️ 1. Loss 계산하기 : Forward propagation

  • ht=tanh⁡(Wxhxt+Whhht−1)h_t = \tanh(W_{xh} x_t + W_{hh} h_{t-1})
    • 각 weight 곱하고 더한 값을 -1~1 사이로 정규화한 hidden state (vector)
  • y^t=softmax(Whyht)\hat{y}_t = \text{softmax}(W_{hy} h_t)
    • Hidden state에 weight 곱하고 0~1 사이로 정규화한 예측값
  • LtL_t
    • yty_t와 y^t\hat{y}_t 차이
    • 이 차이를 최소화하는 방향으로 파라미터 업데이트 (Loss function 최소화)
  • One to many, many to many 구조에서는 각 시점별 loss의 평균을 전체 loss로 사용함

✔️ 2. Gradient 계산하기 : Backward propagation

  • 갱신된 파라미터를 업데이트하는 방법
  • 파라미터를 얼마나 업데이트 해야 하는가? → gradient(기여도) 만큼
  • Backward Propagation Trough Time (BPTT) in RNN
    • BPTT를 통해 gradien산

Ⅰ.

∂Loss∂Why=∂Lt∂y^t×∂y^t∂Whyht×∂Whyht∂Why\frac{\partial \text{Loss}}{\partial W_{hy}} = \frac{\partial L_t}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial W_{hy}h_t} \times \frac{\partial W_{hy}h_t}{\partial W_{hy}}

Why 파라미터 업데이트
: Loss의 Why에 대한 미분값(gradient)을 현재 값에 더하거나 빼 줌

Ⅱ.

∂Loss∂Whh=(∂Loss∂y^t×∂y^t∂h3×∂h3∂Whh)+(∂Loss∂y^t×∂y^t∂h3×∂h3∂h2×∂h2∂Whh)+(∂Loss∂y^t×∂y^t∂h3×∂h3∂h2×∂h2∂h1×∂h1∂Whh)\frac{\partial \text{Loss}}{\partial W_{hh}} = (\frac{\partial \text{Loss}}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial h_3} \times \frac{\partial h_3}{\partial W_{hh}}) + (\frac{\partial \text{Loss}}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial h_3} \times \frac{\partial h_3}{\partial h_2} \times \frac{\partial h_2}{\partial W_{hh}}) + (\frac{\partial \text{Loss}}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial h_3} \times \frac{\partial h_3}{\partial h_2} \times \frac{\partial h_2}{\partial h_1} \times \frac{\partial h_1}{\partial W_{hh}})

Whh 파라미터 업데이트
: Loss의 Whh에 대한 미분값(gradient)을 현재 값에 더하거나 빼 줌

🟡 첫번째 괄호 (T3) : T3(시점 3)에서의 영향
🟡 두번째 괄호 (T2) : T3으로부터 전해진 영향 고려
🟡 세번째 괄호 (T1) : T2로부터 전해진 영향 고려

Ⅲ.

∂Loss∂Wxh=(∂Loss∂y^t×∂y^t∂h3×∂h3∂Wxh)+(∂Loss∂y^t×∂y^t∂h3×∂h3∂h2×∂h2∂Wxh)+(∂Loss∂y^t×∂y^t∂h3×∂h3∂h2×∂h2∂h1×∂h1∂Wxh)\frac{\partial \text{Loss}}{\partial W_{xh}} = (\frac{\partial \text{Loss}}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial h_3} \times \frac{\partial h_3}{\partial W_{xh}}) + (\frac{\partial \text{Loss}}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial h_3} \times \frac{\partial h_3}{\partial h_2} \times \frac{\partial h_2}{\partial W_{xh}}) + (\frac{\partial \text{Loss}}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial h_3} \times \frac{\partial h_3}{\partial h_2} \times \frac{\partial h_2}{\partial h_1} \times \frac{\partial h_1}{\partial W_{xh}})

Wxh 파라미터 업데이트
: Loss의 Wxh에 대한 미분값(gradient)을 현재 값에 더하거나 빼 줌

🟡 괄호 내용 위와 동일
🟡 각 시점마다의 gradient를 구한 다음 모두 더하면 됨

✅ Gradient 계산 정리

∂Loss∂Why=∂Lt∂y^t×∂y^t∂Whyht×∂Whyht∂Why\frac{\partial \text{Loss}}{\partial W_{hy}} = \frac{\partial L_t}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial W_{hy}h_t} \times \frac{\partial W_{hy}h_t}{\partial W_{hy}}
∂Loss∂Whh=∑k=0t(∂L∂y^t×∂y^t∂ht×∂ht∂hk×∂hk∂Whh)\frac{\partial \text{Loss}}{\partial W_{hh}} = \sum_{k=0}^{t} \left( \frac{\partial L}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial h_t} \times \frac{\partial h_t}{\partial h_k} \times \frac{\partial h_k}{\partial W_{hh}} \right)
∂Loss∂Wxh=∑k=0t(∂L∂y^t×∂y^t∂ht×∂ht∂hk×∂hk∂Wxh)\frac{\partial \text{Loss}}{\partial W_{xh}} = \sum_{k=0}^{t} \left( \frac{\partial L}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial h_t} \times \frac{\partial h_t}{\partial h_k} \times \frac{\partial h_k}{\partial W_{xh}} \right)

회귀 문제 : Loss function (MSE) = 1N∑i=1N(yi−y^i)2\frac{1}{N} \sum_{i=1}^{N} (y_i - \hat{y}_i)^2
분류 문제 : Loss function (Cross Entropy) = ∑c=1Myo,clog⁡(po,c)\sum_{c=1}^{M} y_{o,c} \log(p_{o,c})

✔️ 3. Parameter Update (학습)

  • 파라미터들을 어떻게 더 좋은 수치로 업데이트할지?
  • 방향 : Loss를 줄이는 방향
  • 학습 정도 : Gradient 만큼 → Gradient Descent
  • 학습률(ɳ, learning rate) : 기여도를 얼마나 반영할 것인지 결정 (예, 0.01)

Why의 gradient 업데이트 : Whynew=Whyold−η⋅∂Loss∂WhyW_{hy}^{new} = W_{hy}^{old} - \eta \cdot \frac{\partial \text{Loss}}{\partial W_{hy}}
Whh의 gradient 업데이트 : Whhnew=Whhold−η⋅∂Loss∂WhhW_{hh}^{new} = W_{hh}^{old} - \eta \cdot \frac{\partial \text{Loss}}{\partial W_{hh}}
Wxh의 gradient 업데이트 : Wxhnew=Wxhold−η⋅∂Loss∂WxhW_{xh}^{new} = W_{xh}^{old} - \eta \cdot \frac{\partial \text{Loss}}{\partial W_{xh}}



4. RNN 한계점

  • 장기 의존성 문제 (long-term dependency problem)
    • 장기 과거 데이터는 h100가 의존하는 h99이 의존하는 h98이 의존하는 ... 형태
  • Sequence의 길이가 길수록, 과거 정보 학습에 어려움이 발생
    • 원인 : 기울기 소실 (vanishing gradient)
    • Gradient는 chain rule에 의해 계산되며, 이때 ht=tanh(Wxhxt+Whhht−1)h_t = tanh(W_{xh}x_t + W_{hh}h_{t-1})
    • Hidden vector들은 tanh 함수로 되어 있음
    • 오래 전 시점들의 Gradient들은 수 많은 시점들의 hidden vector에 한 그 전 시점의 hidden vector 미분값으로 표현되어 있음
    • 즉, 오래 전 시점들의 gradient들은 tanh 함수의 미분으로 표현되어 있음
    • tanh 함수를 미분하면 함수값은 0~1 사이(소수)에 해당되는데,
    • 오래 전 시점들의 소수를 매우 많이 곱하면, gradient는 결국 0에 수렴함
    • 이는 현재 시점 업데이트가 되지 않는 것임 (loss function 최소화 불가능)
    • 장기 과거 시점에 대한 모델 학습이 안 됨
  • RNN 개선 모델 : LSTM (Long Short-Term Memory)
profile
Joo
적당히 공부한 거 정리하는 곳
이전 포스트

시계열) ARIMA 분석 기법

다음 포스트

시계열) LSTM

0개의 댓글