🐼 목 차 🐼
1. ACF
2. PACF
3. AR model
4. MA model
5. ARMA model
6. 차분 (non-stationary를 stationary로)
7. ARIMA(Autoregressive Integrated Moving Average) model
8. (번외) SARIMA(Seasonal ARIMA)
시계열 데이터 분석 기법에는 크게 통계 기법, 머신러닝 기법, 딥러닝 기법이 있다.
이 중 나는 통계 기법 중 ARIMA를 접해본 적이 없어서 알아보려고 한다.
먼저, 직전 포스팅에서는 정상성 만족 여부(일정한 평균과 분산)를 판별하는 기법에는 크게 통계적 기법과 그래프를 통해 직관적으로 확인하는 방법(ACF/PACF 그래프)이 있다고 정리했다.
우선 ARIMA 모델을 알아보기 전에, ACF와 PACF를 이해해보자.
1. ACF
보다 복잡한 시계열 데이터는 정상성 만족 여부를 단순히 그래프를 통해 파악하는 것은 힘듦(randomness, noise)
이 경우, ACF(Autocorrelation Function)를 계산해 시차(lag)에 따른 자기 상관 계수를 확인하면 데이터가 얼마나 이전 관측치와 상관성을 갖는지를 파악할 수 있음
→ 정상성을 갖는 시계열 데이터의 ACF는 시차에 관계없이 지속적으로 0 주변에서 랜덤하게 변동하므로, 이를 통해 정상성을 확인할 수 있음
※ Autocorrelation : 시계열적 관점으로 보았을 때, time shifted된 자기 자신과의 상관성
- ACF(자기상관함수)란?
- 시차에 따른 일련의 자기 상관을 측정하는 함수이며, 시차가 커질수록 ACF는 0에 수렴함
- 정상 시계열은 상대적으로 빠르게 0에 수렴하며, 비정상 시계열은 천천히 감소하고, 종종 큰 양의 값을 가짐
- MA 최적 차수(q)를 구하는 데 사용
- 0으로 수렴하게되는 시점을 q값으로 잡을 수 있음 (신뢰구간에 진입하는 최초의 시점)
- 시계열 데이터가 MA의 특성을 띄는 경우 ACF는 급격히 감소함위는 ACF 식인데,
Yt와Yt+k사이의 상관 관계를 나타내는 식임 (시차k에 대한 공분산 / 시계열 전체에 대한 분산)
일반적인 상관 계수의 식과 매우 유사함
점진적으로 증가하는 추세(trend)가 보이기 때문에, 정상성을 갖지 않음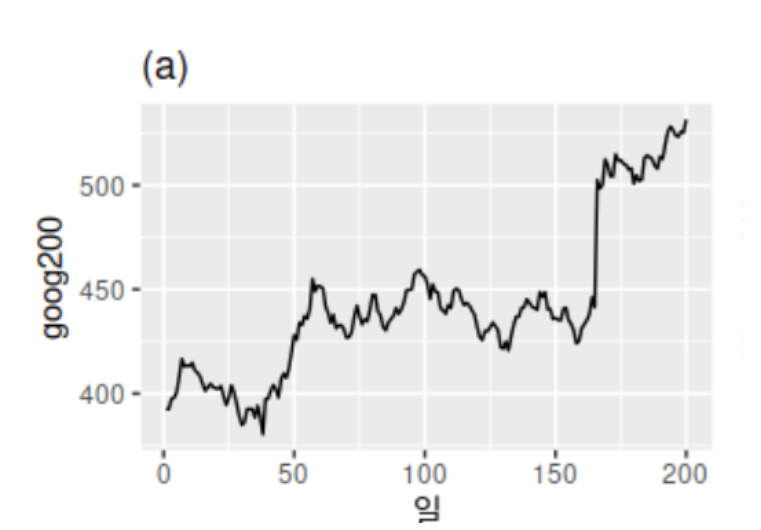
이 데이터를 ACF로 그려보면, 아주 느리게 감소하는 걸 확인할 수 있음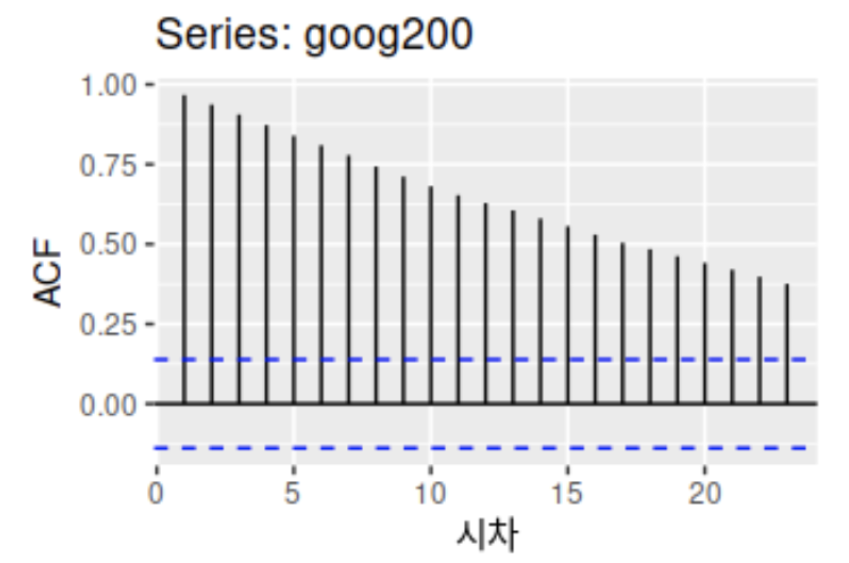
차분 후 정상 시계열로 변환하니 ACF가 훨씬 0에 가깝고 비교적 빠르게 0에 수렴함(모두 파란 영역 안에 들었음)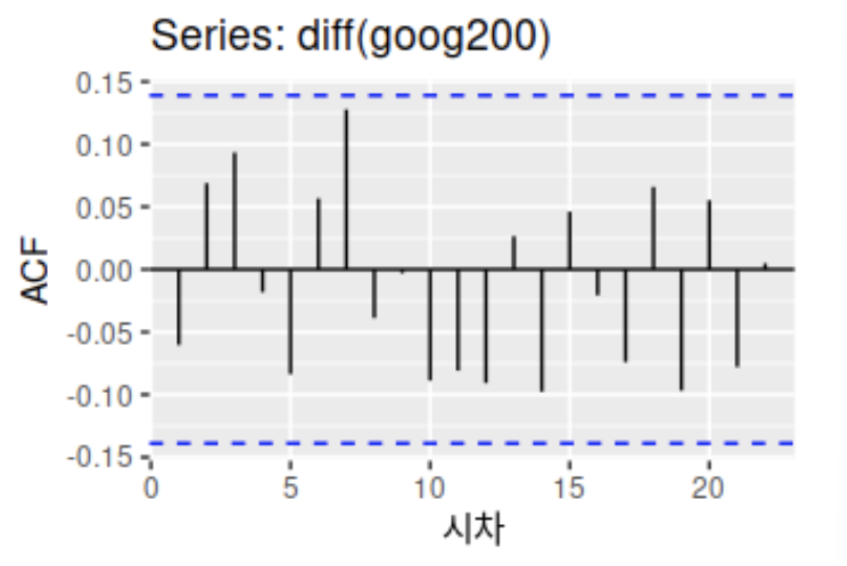
2. PACF
시계열에는 시차를 제외하고도 다양한 변수들이 존재할 수 있음
이 다른 변수를 제거해야 순수한 시차에 따른 상관성을 확인할 수 있음 → 이를 위해 PACF 사용
- PACF(편자기상관함수)란?
- 특정 시차의 자기상관성(ACF)에서 다른 시차의 자기상관성을 제거한 값
- 시차 간의 간접적인 관계(상관성)를 분석해 예측 모형의 차수(lag의 개수)를 결정함
- AR 모델(후술) : 이전 시차의 관측치를 몇 개 사용할 것인가
- MA 모델(후술) : 이전 시차의 예측 오차를 몇 개 사용할 것인가
- 일반적으로 MA 모형에서는 ACF 그래프에서 자기상관이 유의한 시차를 고려해 차수를 결정함
- AR 최적 차수(p)를 구하는 데 사용
- 0으로 수렴하게되는 시점을 p값으로 잡을 수 있음 (신뢰구간에 진입하는 최초의 시점)
- 이론적으로는 PACF가 0이 되어야 하지만, 실제로는 다소 진동하는 패턴을 보임
- 샘플 크기가 특히 작을 때, 혹은 다른 요인들(예, 무작위 변동, 추정 오차 등)에 의해 진동하는 패턴을 보임
- 시계열 데이터가 AR의 특성을 띄는 경우 PACF는 급격히 감소함
ACF/PACF 그래프에서 정상성 만족 여부 파악하는 법
✅ ACF/PACF 그래프에서 일정한 패턴이 없거나 갑자기 떨어지는 패턴 → 정상성
✅ ACF/PACF 그래프에서 시차에 따라 일정하게 천천히 떨어지거나 올라갔다, 내려갔다 하는 패턴 → 비정상성
3. AR(Autoregressive) model
앞의 절에서 다룬 ACF와 PACF를 활용해 시계열 데이터의 자기상관성을 파악하고, AR 모형과 MA 모형(다음 절)의 차수를 결정해, 데이터를 예측하거나 분석할 수 있음
-
AR 모형이란?
- 자기 회귀 모형
- 정상성을 가진 데이터에 사용
- 자기상관성을 시계열 모형으로 구성하였으며, 예측하고자 하는 특정 변수(Y)의 과거 관측값들(Y lag)의 선형결합으로 해당 변수의 미래값을 예측하는 모형
- 종속 변수인
Y의 lag를 설명 변수인X로 사용- hyperparameter :
p
- hyperparameter :
- 이전 자신의 관측값이 이후 자신의 관측값에 영향을 준다는 아이디어에 기반 (자기상관성)
-
다중 선형 회귀와의 차이점
- 자기자신을 갖고 모델링하기 때문에 독립성 X
- 계수(intercept)를 추정할 때 일반적으로 사용했던 최소제곱법은 사용할 수 없음
4. MA(Moving Average) model
- 예측 오차를 이용해 미래를 예측하는 모형
- 과거와 현재 자신의 오차(백색 잡음)와의 관계
- 자기 자신을 종속변수 y로 하고, 에러들을 설명 변수로 갖음
- 정상성을 가진 데이터에 사용
- t 시점의 데이터(yt)를 t 시점의 에러()와 그 과거의 에러들로 표현
- hyperparameter :
q
- hyperparameter :
5. ARMA(Autoregressive and Moving Average) model
- AR과 MA를 합친 모델
- 시계열 데이터의 자기회귀와 이동평균 요소를 모두 고려해 다음 값을 예측
- t 시점의 데이터(yt)를 자기자신의 lag된 값들, t 시점의 에러와 전 시점의 error들로 표현함
- hyperparameter :
p,q
- hyperparameter :
- 정상성을 가진 데이터에 사용
✔️ AR, MA, ARMA 모형을 구현하기 위해서는 데이터가 stationary해야 함
✔️ 일반적인 상황에서의 데이터는 non-stationary한 데이터가 더 많으므로, 이를 stationary하게 바꿔줘야 함
✔️ 그 방법이 이전 포스트에서 다룬 차분(differencing)
6. 차분 (non-stationary를 stationary로)
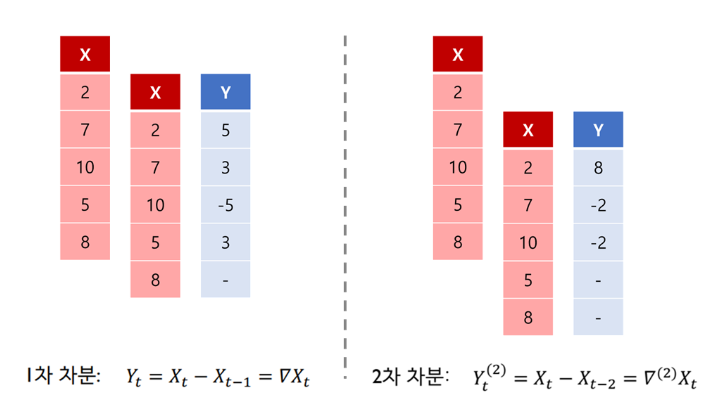
- 차분(differencing) : 원래 데이터와 그것을 shift한 것을 뺀 결과
- 1차 차분 : t 시점의 데이터와 t-1 시점 데이터의 차이
- 2차 차분 : t 시점의 데이터와 t-2 시점 데이터의 차이
- d차 차분 : t 시점의 데이터와 t-d 시점 데이터의 차이
- 일반적으로 시계열 곡선이 특정한 트렌드를 보이면 1차 차분을, 시간에 따라 들쑥날쑥한 트렌드를 보이면 2차 차분을 수행함
- 대부분의 데이터가 2차 차분으로 충분함
- 3차 차분까지 수행해야 stationary가 되는 데이터는 AR, MA, ARMA 모델로는 적합하지 않은 데이터임 (ARIMA 사용)
7. ARIMA(Autoregressive Integrated Moving Average, 자기회귀누적이동평균) model
- 현재와 추세간의 관계
- 앞서 설명한 AR, MA, ARMA 모델은 데이터가 stationary인 경우에만 사용할 수 있음
- 비정상인 경우는 차분을 통해 데이터를 정상으로 변형해야 함 (대부분의 데이터는 비정상)
- ARIMA는 ARMA 모델에 d회 차분을 수행한 모델임
- 비정상 데이터를 차분을 통해 정상 데이터로 변환한 후, ARMA 모델을 적용해 차수를 결정함
- 정상성을 만족했다는 가정 하에서, AR와 MA 차수 결정은 ACF, PACF 그래프를 보고 결정함
- hyperparameter :
p,q,d
-d는d차 차분과 같이 time shift를 얘기함
✅ ACF, PACF의 모양을 통해 ARIMA(AR, MA, ARMA) 모델의 하이퍼파라미터인 p와 q를 결정하는데 그 방법은 아래의 표와 같음
| Model | ACF | PACF |
|---|---|---|
| MA(q) | q번째 lag 이후 급격히 0으로 수렴 q+1번째 lag부터는 해당 시계열 값들이 서로 상관성이 없음 | 지수적으로 감소, 소멸하는 사인함수 형태 |
| AR(p) | 지수적으로 감소, 소멸하는 사인함수 형태 | p번째 lag 이후 급격히 0으로 수렴 p+1번째 lag부터는 해당 시계열 값들이 서로 상관성이 없음 |
| ARMA(p,q) | (q-p)번째 lag 이후부터 소멸 | (q-p)번째 lag 이후부터 소멸 |
8. (번외) SARIMA(Seasonal ARIMA)
대부분의 시계열 데이터는 비정상적일 뿐만 아니라 계절성 또한 갖고 있음
그런 데이터의 경우 SARIMA도 고려해 볼 수 있음
- ARIMA 모델의 변형 (Trend와 seasonality를 고려함)
- ARIMA 모델과 ACF/PACF에서 AR, MA 차수를 결정해야 하는 것은 유사하지만, 그것이 계절성 시차만큼 벌어진다는 것에 차이가 있음
- 일반적으로 차분할 때 계절성 차분 → 일반 차분 순으로 진행하는 것이 좋음
- ACF/PACF 그림을 보고 최적 모델을 하나로 결정하기 어려워, 여러가지로 돌려보며 확인하는 과정이 필요함
참조
- https://www.youtube.com/watch?v=ma_L2YRWMHI
- https://assaeunji.github.io/statistics/2021-09-08-arimapdq
- https://otexts.com/fppkr/non-seasonal-arima.html
- https://velog.io/@isitcake_yes/mlarimastockprediction
- https://teddylee777.github.io/data-science/time-series
- https://byeongkijeong.github.io/ARIMA-with-Python
- https://assaeunji.github.io/statistics/2021-09-08-arimapdq - autoarima 참조
