엔트로피와 지니 계수

Decision Tree의 분할 기준 (Split Criterion)

정보 획득 (Information Gain)

• 정보의 가치를 반환하는 데 발생하는 사전의 확률이 작을수록 정보의 가치는 커진다.
• 정보 이득이란 어떤 속성을 선택함으로 인해서 데이터를 더 잘 구분하게 되는 것

엔트로피

• 열역학 용어로 물질의 열적 상태를 나타내는 물리량의 단위 중 하나 (무질서의 정도)
• 정보 엔트로피는 위의 엔트로피 개념에서 힌트를 얻어, 확률 분포의 무질서도나 불확실성 혹은 정보 부담 정도를 나타냄
  $-p_i \log_2 p_i$
  $Entropy = \sum_{k=1}^{d} R_i \left( \sum_{k=1}^{m} -p_i \log_2 p_i \right)$

  

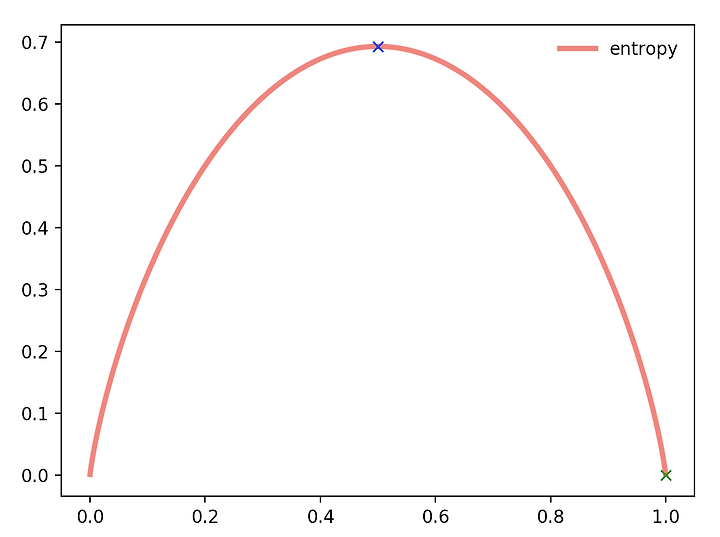
$P$는 해당 데이터가 해당 클래스에 속할 확률이며 아래의 그래프는 엔트로피 그래프임
어떤 확률 분포로 일어나는 사건을 표현하는 데 필요한 정보의 양이고,
이 값이 커질수록 확률 분포의 불확실성이 커지며, 결과에 대한 예측이 어려워짐
엔트로피는 이 확률들의 합이다! (정보가 많을수록 낮은 엔트로피)
※ 참고로 $R_i$는 특정 노드 $i$ 에 속하는 샘플의 비율을 지칭함 (정보를 쪼갰을 때, 특정 집단에 속할 비율)

지니 계수 (불순도율)

엔트로피의 계산량이 많아(log 계산) 보다 계산량이 적은 지니 계수를 사용하는 경우가 많음
엔트로피와 지니 계수 둘 다 낮을수록 better