[STATS] MLE

우도를 최대화하는 모수를 찾는 방법인 MLE는 통계학에서 매우 중요하게 다뤄지는 개념이다. AI/ML에서도 적용되는 개념이니 잘 알아두면 좋을 거 같다.

Likelihood

우도(가능도, Likelihood)는 어떤 모델과 데이터가 주어졌을 때, 이 모델이 데이터를 얼마나 잘 설명하는지에 대한 수치화된 척도이다.

확률은 고정된 분포에서 관측값이 관측될 확률인 반면에, 우도는 고정된 관측값이 해당 확률분포에서 나왔을 확률이다. 즉, 확률과 우도를 구분하기 위해서는 고정된 것이 무엇이냐에 주목할 필요가 있다.

우도의 정의에 의해, $\theta$에 대한 함수인 우도 함수는 확률 분포가 아니며 합이 1이 아닐 수 있음을 알 수 있다. $n$번의 독립 시행을 거쳐 얻은 데이터에 대한 우도는 모델에 관측된 데이터를 모두 넣어 각각에 대한 확률을 산출하고, 얻어낸 확률들을 모두 곱합으로써 얻을 수 있다.

likelihood function은 다음의 식으로 정의된다.

계산할 때는 주로 likelihood function에 로그를 취한 log-likelihood function을 이용하게 된다.

Example

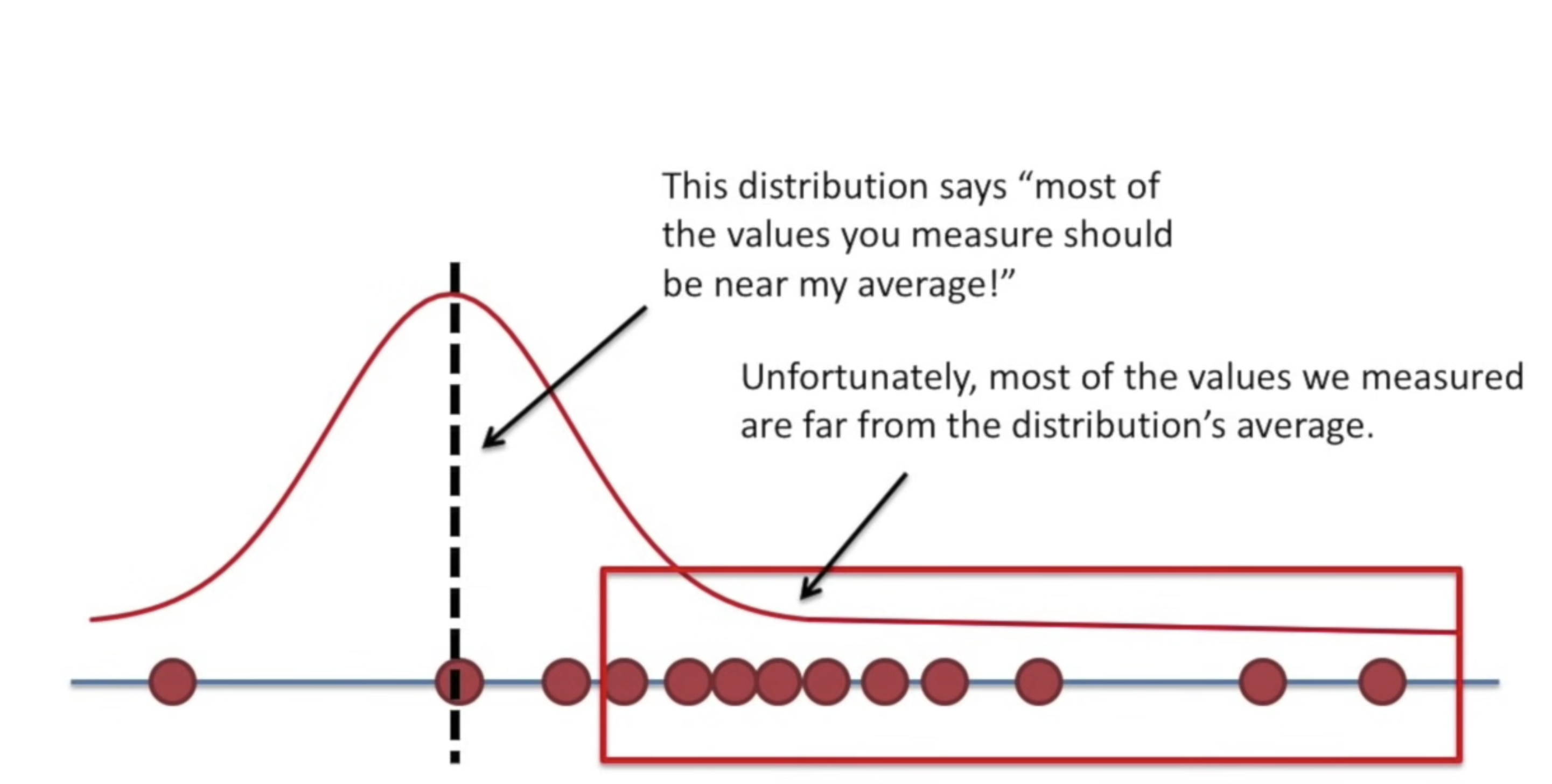
위 정규분포의 평균은 실제 관측값의 평균과 다르고, 이에 대부분의 관측값은 분포의 평균과 떨어져있음을 볼 수 있다. 이 때, 분포의 꼬리 쪽에 위치한 관측값들의 우도는 낮다고 할 수 있다.

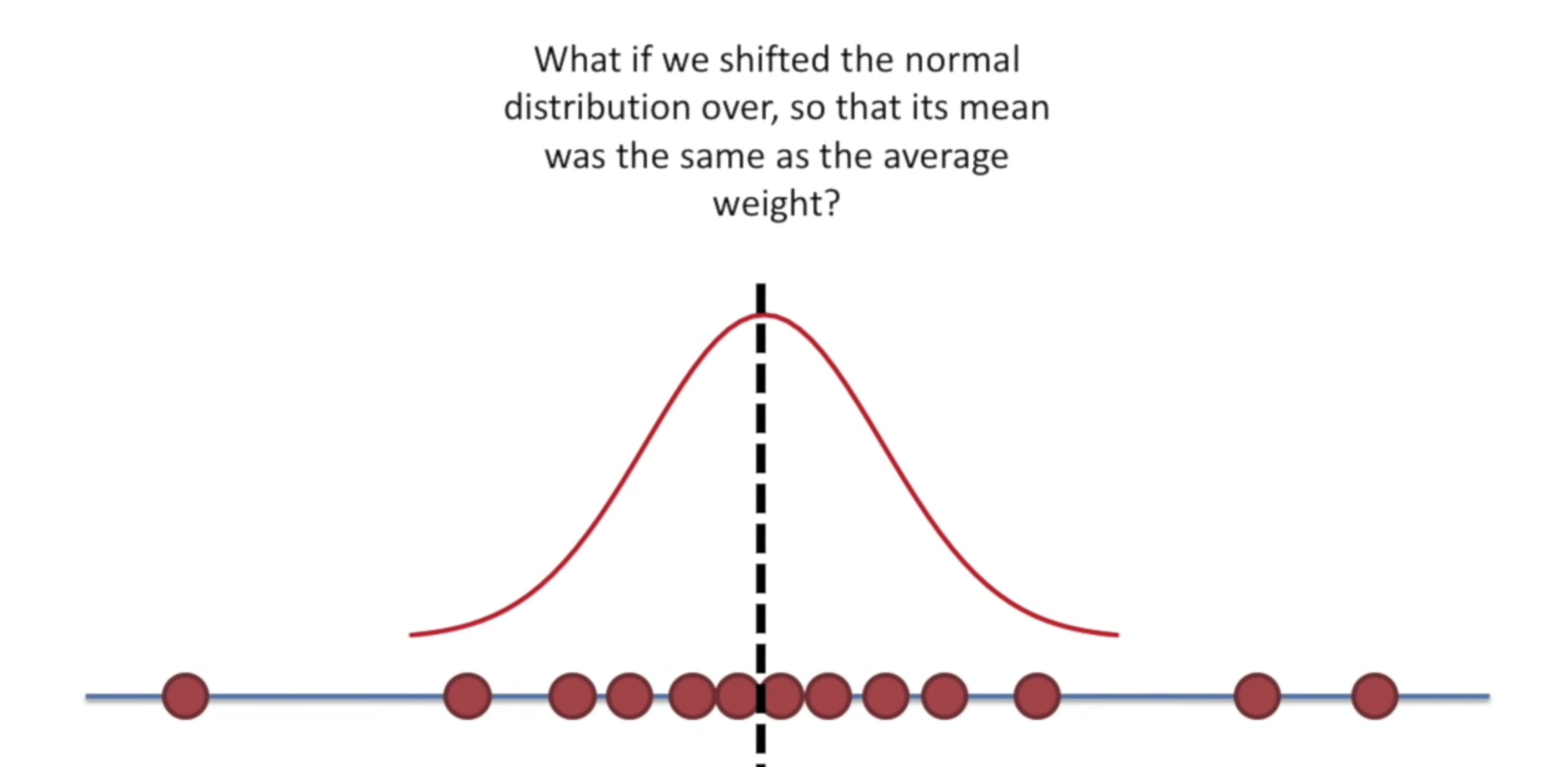
정규분포를 위와 같이 움직이게 되면, 분포의 평균과 실제 관측값이 평균이 일치하게 된다. 평균값이 정규분포를 따르게 되면, 해당 관측값들의 우도 또한 높아지게 된다.

Maximum Likelihood Estimation

명칭에서 알 수 있듯이, MLE(최대우도법)는 Likelihood function의 최댓값을 찾는 방법이다.

함수의 최댓값을 찾을 때 주로 미분계수를 이용하는 것과 같이, 앞서 정의한 $l(\theta| x)$를 파라미터 $\theta$에 대해서 편미분하고 그 값이 0이 되도록 하는 값을 찾으면, 그 값이 바로 $\hat{\theta}$이다.

Characteristics

• Aympototically optimal
• Following standard normal distribution as n goes to infinity
• Equivalent
• Not unbiased, but consistent
  
  

Example

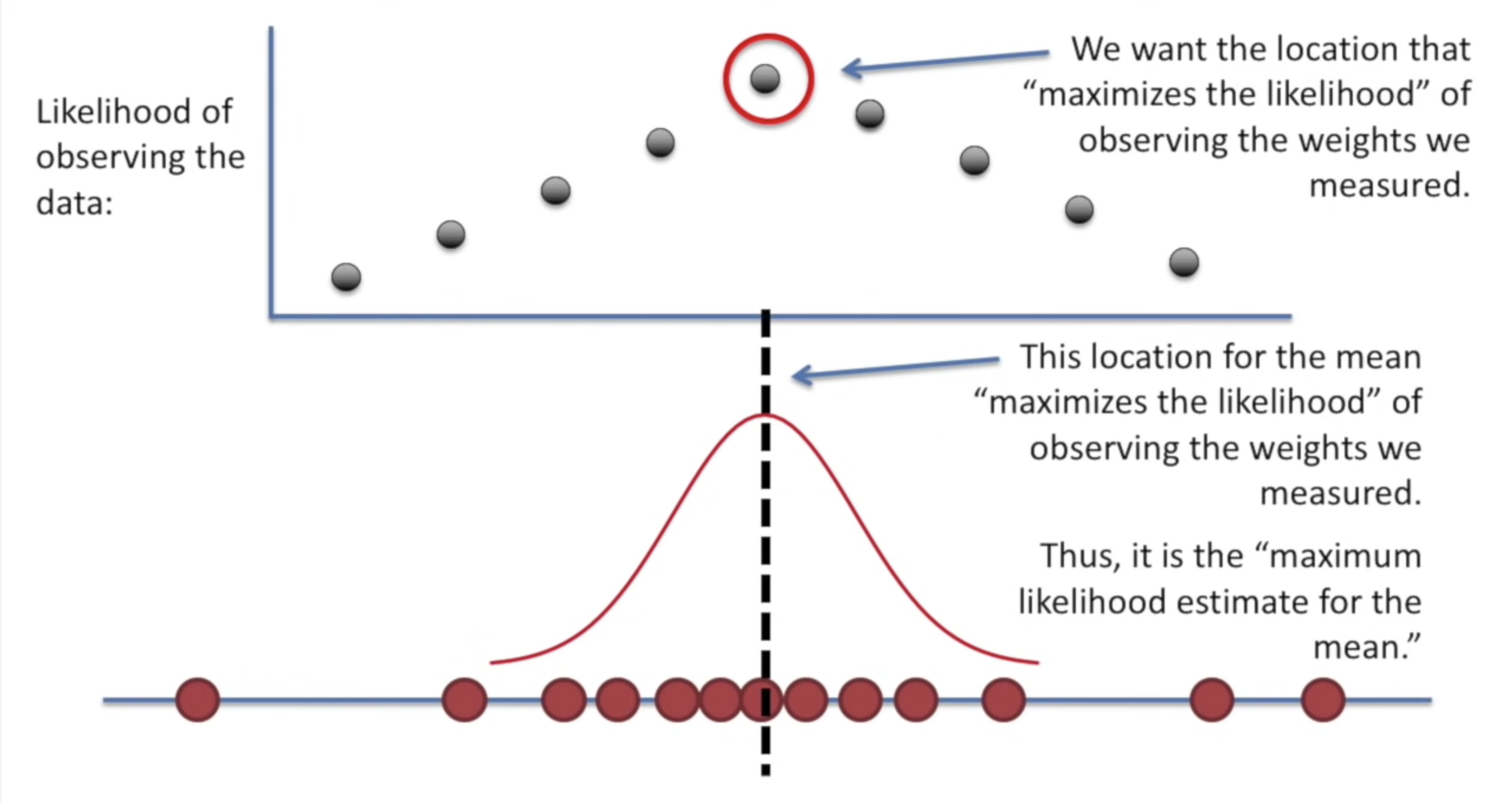
분포의 중심 위치를 기준으로 데이터의 우도를 표시함으로써 측정된 관측값의 우도를 최대화할 수 있는 위치를 찾을 수 있다. 이 평균의 위치는 관측값의 우도를 최대화하고, 이는 MLE로 찾은 평균이다.

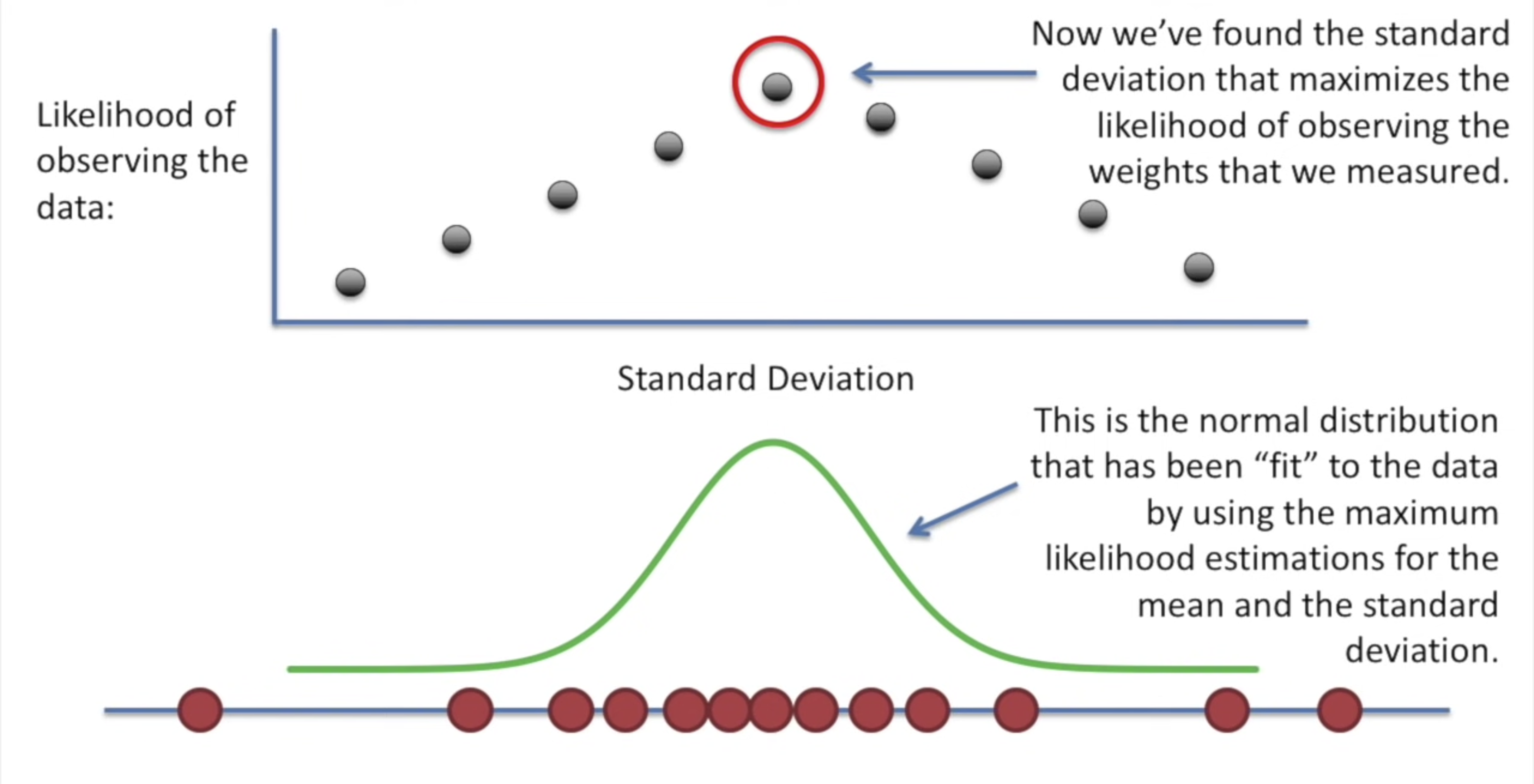
평균뿐만 아니라 위와 같이 표준편차를 구할 수도 있으며, 그 외에도 다양한 모수를 구하는 데 최대우도법을 이용할 수 있다.

Addition

Cramer-Rao lower bound 이론을 이용해 $\hat{\theta}$(mle of $\theta$)가 efficient estimator인지 판단할 수 있다.

Reference

https://youtu.be/XepXtl9YKwc