정보 이론과 엔트로피

보통 엔트로피(Entropy)라 하면, 머릿속에 가장 먼저 떠오르는 것은 과학에서 다루는 열역학적 엔트로피이다. 열역학적 관점에서의 엔트로피는 "물체의 열적 상태를 나타내는 물리량의 하나"이다.

이러한 과학적 정의는 차치하고, 통계학에서 정의하는 엔트로피에 대해 알아보고자 한다. 엔트로피는 정보이론의 기초가 되며, 정보이론은 NLP와 CV 뿐만 아니라 다양한 ML 기법의 뼈대가 되므로 모델을 정확히 이해하고 연구하기 위해서는 꼭 선행되어야 할 개념이라고 생각한다. 우리가 늘상 이야기하는 IT 또한 Information Technology의 약자로, 그만큼 현시대에 있어 정보(Information)의 중요성은 어마무시하다는 사실을 잊지 말자.

Communication

Communication은 끝에서부터 다른 끝까지의 정보 전달이다. 보통은 시작 지점을 Transmitter, 그리고 수신하는 지점을 Receiver라고 한다. 그리고 이 사이에는 물리적인 미디엄 Channel이 존재한다.

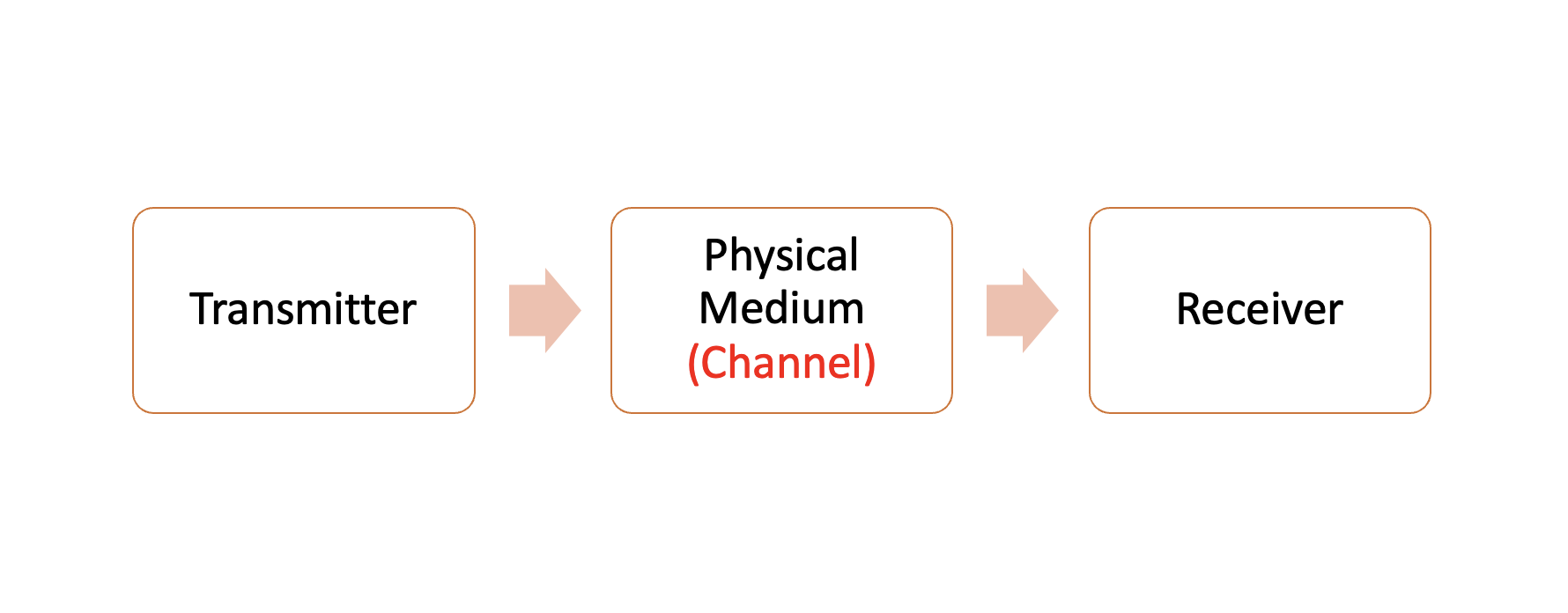
대화 또한 정보 전달의 일종이다. 시대가 변화하면서 봉화대와 같은 연기 신호, 전화기, 라디오, TV 등이 차례대로 등장했다.

참고로 유선 전화기와 같은 경우는 Channel이 Wire가 된다.

과거에는 대부분의 정보 전달이 아날로그로 이루어졌다. 당시대에 살았던 섀넌(Shannon)은 이러한 아날로그 시대에 안주해서는 안 되고, ad-hoc approach의 통합을 요했다.

Shannon's Questions

1. Is there a general methodology for designing communication systems?

2. Is there a common currency of information?

3. Is there a limit to how fast one can communicate?

이러한 세 가지 질문들을 한 번에 해결한 것이 바로 Communication Architecture이고, 이렇게 등장한 것이 Information Entropy(Shannon Entropy)이다.

Communication Architecture

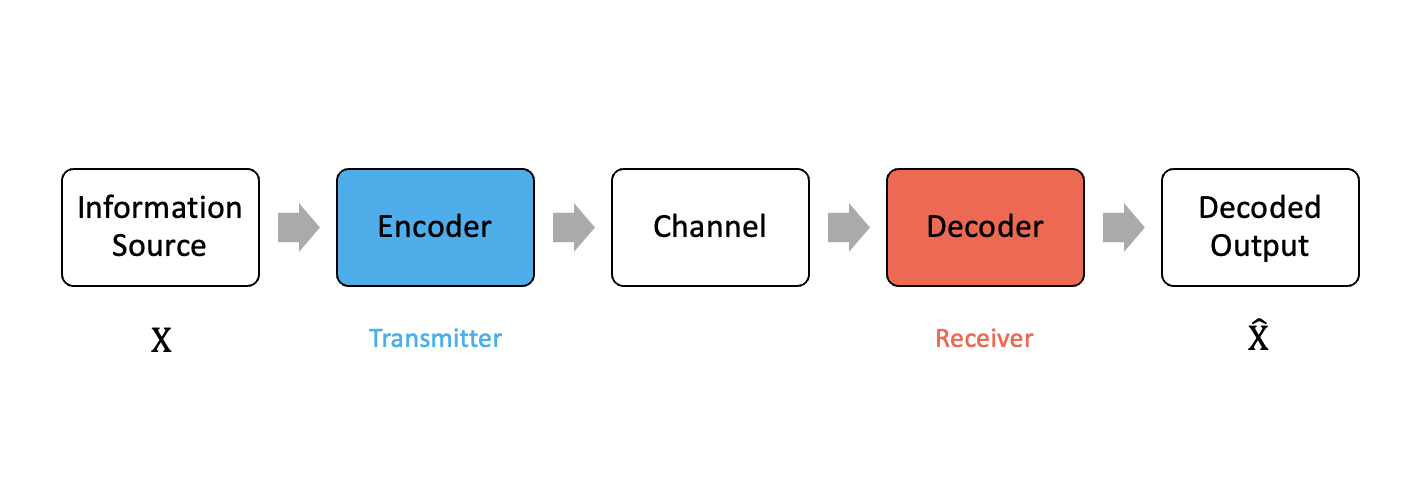
정보이론에서 가장 주가 되는 도식이다. Information source $X$가 인코더(Encoder)를 통해 암호화 되고, 다시 Decoder를 거치며 복호화 되어 $\hat{X}$이라는 결과가 도출된다. 물론 해당 아키텍처가 효용이 있기 위해서는, Information source인 $X$와 일련의 정보 전달 과정을 거친 $\hat{X}$이 일치해야 한다.

• Information Source
  정보는 문자, 소리, 이미지 등이 될 수 있다. 통계학에서 증명을 위해서는 대표적으로 알파벳(A, B, C,...)을 사용한다.

• Encoder
  인코더를 통해서 정보가 신호로 변환된다. 정확히는 인코더가 Source Encoder와 Channel Encoder로 구분되는데, Source Encoder를 거치며 비트(bit)로 변환되고, 이는 엔트로피의 기본 단위가 된다.
  

• Channel
  채널은 신호를 전달하는 매개체와 같은 역할을 한다.

• Decoder
  인코더를 거치며 변환된 신호를 다시 일종의 메시지(정보)로 변환해주는 역할을 한다.

• Decoded Output
  디코더를 거쳐서 나온 정보이다. 우리는 가능한 모든 결과에 있어서 $\hat{X}=X$가 성립하길 기대하며, 해당 조건이 만족되었을 때 우리는 Successful decode라 정의한다.
  

Encoder

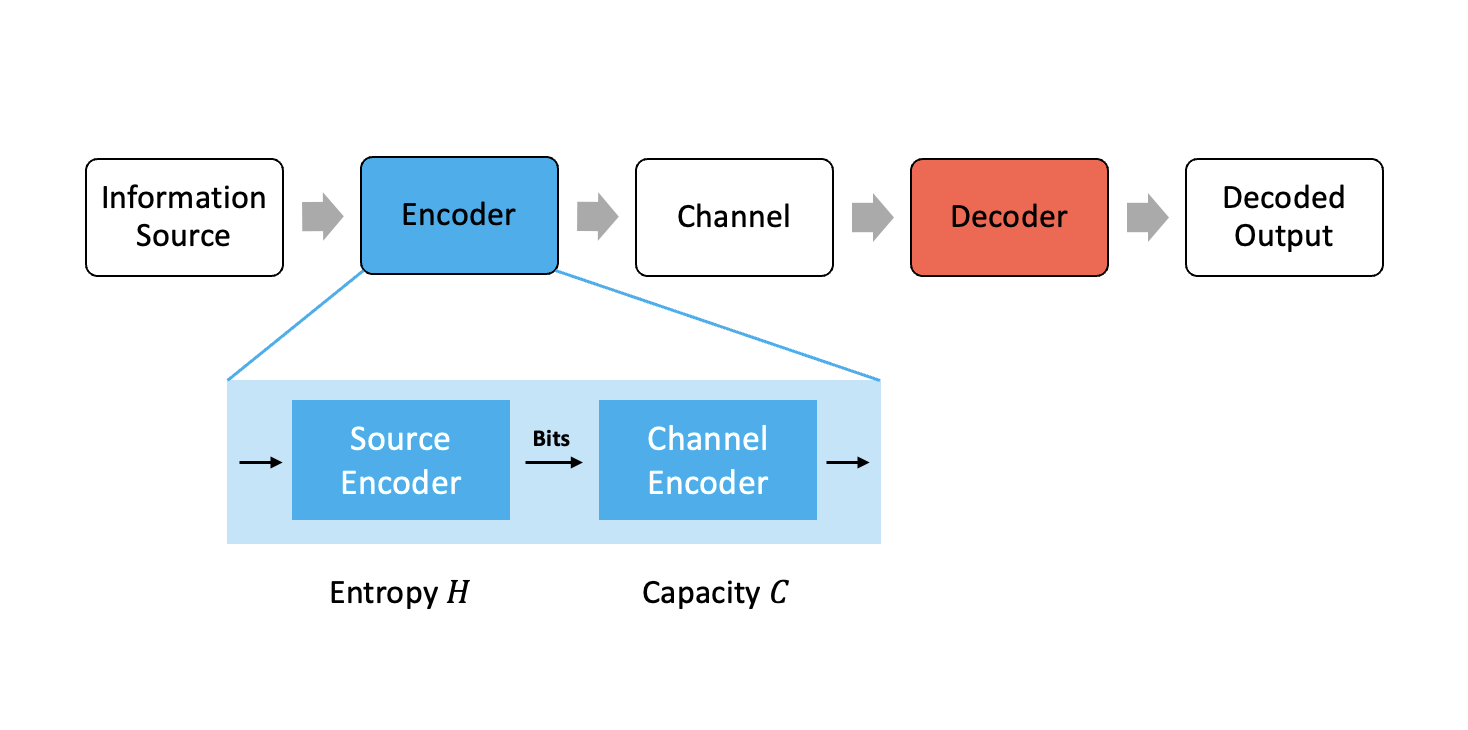
• Entropy $H$
  Source Encoder의 output은 Entropy $H$이다. Entropy $H$는 소스를 나타내는 최소 비트 수를 의미한다. 이는 소스 코딩 정리(Source Coding Theorem)를 통해 증명되며, 데이터 압축(Data Compression)과도 관계가 있다.

• Capacity $C$
  Channel Encoder의 output인 Capacity $C$는, 채널을 통해 안정적으로 통신할 수 있는 최대 비트 수를 의미한다. 이는 채널 코딩 정리(Channel Coding Theorem)을 통해 증명된다.
  

위 두 인코더는 데이터가 치명적인 오류 없이 압축되고 디코더를 거치며 산출된 추정치가 기존의 정보와 일치하기 위해 필수적이다.

그렇다면 정보 이론의 주축이 되는 엔트로피란 무엇일까?

Entropy

엔트로피는 확률 변수의 불확실성(Uncertainty)을 측정한 지표이다. 불확실성은 비트의 개수(# of bits)로 정량화된다. 엔트로피 $H(X)$의 정의는 다음과 같다.

위 식은 $\sum_{x\in\chi}p(x)\log {1 \over p(x)}$로 표현될 수 있으며, 여기서 $\log {1 \over p(x)}$를 function of p(x)로 보면, $\mathbb{E}[\log {1 \over p(x)}]$와 같이 기댓값으로 표현할 수도 있다.

Properties

엔트로피의 일반적인 속성은 다음과 같다. 정의를 통해서도 해당 속성들을 유추해볼 수 있다.

• Minimum entropy = 0
• Uniform distribution has the maximum Entropy
• Entropy of uniform distribution = $\log{|x|}$

종합하면 다음과 같은 식이 도출된다.

그리고 해당 식은 다음의 과정을 통해 증명될 수 있다.