Bias(편향) - Variance(분산) Trade-Off

Bias-Variance trade-off 란, 모델링 할 때 error 처리를 위해 중요하게 알아야하는 개념이며, 자주 헷갈릴 수 있다.

Bias (편향)

• 편향은 예측값과 실제값의 차이다.
• 편향이 크다는 것은 예측값-실제값 차이가 크다는 것
  • 이는 "과소적합"을 의미한다.

Variance (분산)

• 분산은 입력에 따른 예측값의 변동성을 의미한다.
• 분산이 크다는 것은 입력에 따른 예측값의 변동성이 크다는 것
  • 이는 "과대적합"을 의미한다.

Trade-off

• Trade-off는 시소처럼 한쪽이 올라가면 한쪽이 내려가는 관계를 의미한다.

[예제 1]

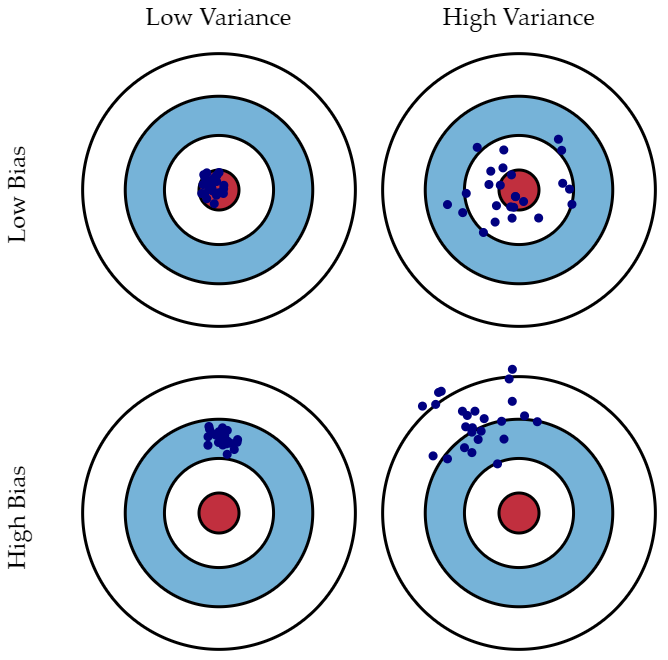
• 파란 점 : 예측값
  빨간 원 : 실제값
• Bias가 높다는 것
  • 예측값-실제값의 오차가 크다는 것 -> "과소적합"
• Variance가 높다는 것
  • 예측값의 변동성이 크다는 것 -> "과대적합"

[예제 2]

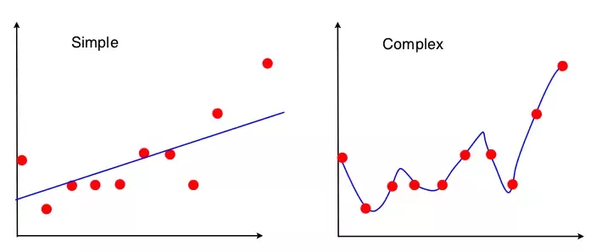
• 왼쪽 그래프 : 큰 bias, 작은 variance
• 오른쪽 그래프 : 작은 bias, 큰 variance

bias 관점

• 왼쪽 그래프의 예측값-실제값 차이는 오른쪽 그래프보다 큼 -> "큰 bias"
• 오른쪽 그래프의 예측값-실제값 차이는 0이다 -> "작은 bias"

variance 관점

• 왼쪽 그래프는 일반화가 잘 되어 있음 -> 예측값이 일정한 패턴 -> "작은 variance"
• 오른쪽 그래프 : 예측 값이 불규칙 패턴 -> "큰 variance"

[예제 3]

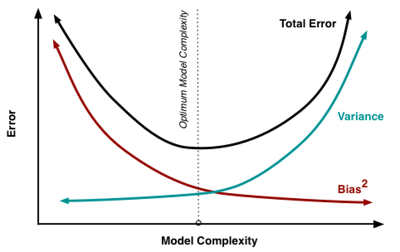
• 모델을 학습 시킬수록 모델의 복잡도는 더 올라간다.
• 그래프의 X축 : 모델 복잡도(model complexity)
• 모델이 단순해질수록, Bias 증가▲, Variance 감소▼
• 모델이 복잡해질수록, Bias 감소▼, Variance 증가▲
• 전체 Error는 Bias와 Variance 간의 Trade-off 관계 때문에, 계속 학습 시킨다고 해도 쉽게 줄어든지 않는다.
• 즉, 무조건 Bias만 줄일 수도, 무조건 Variance만 줄일 수도 없기 때문에, Bias와 Variance의 합이 최소가 되는 적당한 지점을 찾아 최적의 모델을 만들어야한다.

출처
https://wooono.tistory.com/220